Đề thi giữa kì 1 Toán 12 Chân Trời Sáng Tạo có đáp án - Đề 04
-
737 lượt thi
-
21 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số có đồ thị như hình dưới đây.
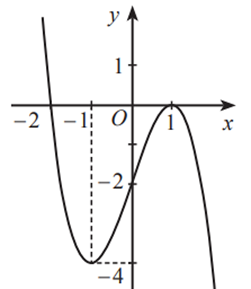
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát hình vẽ, ta thấy trên khoảng \[\left( { - 1;\,\,1} \right)\], đồ thị hàm số \[y = f\left( x \right)\] đi lên từ trái qua phải nên hàm số đã cho đồng biến trên khoảng này.
Câu 2:
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
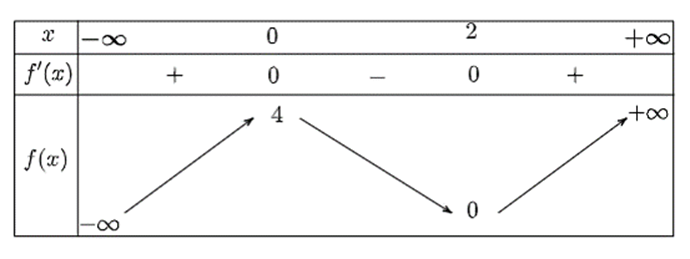
Điểm cực tiểu của hàm số đã cho là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Căn cứ vào bảng biến thiên, ta thấy hàm số đã cho đạt cực tiểu tại điểm \[x = 2\].
Câu 3:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
![Giá trị lớn nhất của hàm số đã cho trên đoạn [-1; 1] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid304-1727781275.png)
Giá trị lớn nhất của hàm số đã cho trên đoạn \[\left[ { - 1;\,1} \right]\] là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Căn cứ vào đồ thị trên, ta thấy \[\mathop {\max }\limits_{\left[ { - 1;\,1} \right]} f\left( x \right) = f\left( 0 \right) = 1\].
Câu 4:
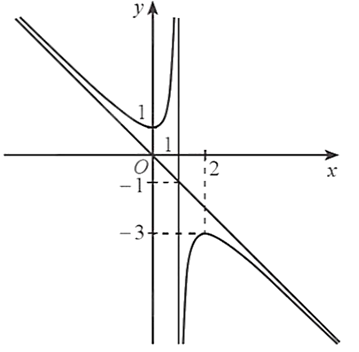
Phương trình đường tiệm cận đứng và phương trình đường tiệm cận xiên của đồ thị đã cho là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát hình vẽ, ta thấy:
+ Đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số đã cho.
+ Đường thẳng \(y = - x\) là tiệm cận xiên của đồ thị hàm số đã cho (\(y = - x\) là đường thẳng đi qua gốc tọa độ và đi qua điểm có tọa độ \(\left( {1;\, - 1} \right)\)).
Câu 5:
Cho hàm số \[y = f\left( x \right)\] có đồ thị là đường cong \(\left( C \right)\) và các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1\); \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 1\); \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2;\,\,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Hỏi mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2;\,\,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\) nên đường thẳng \(y = 2\) là tiệm cận ngang của \(\left( C \right)\).
Câu 6:
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình dưới?
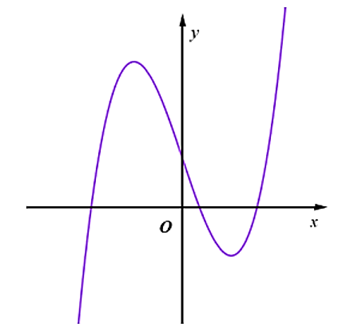
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quan sát đồ thị, ta thấy đây không phải đồ thị hàm số phân thức nên loại phương án A và B.
Còn hai phương án C và D đều là hàm số bậc ba, dạng \(y = a{x^3} + bx + c\).
Ta thấy khi \[x \to + \infty \] thì \(y \to + \infty \) nên hệ số \(a > 0\). Vậy ta chọn phương án D.
Câu 7:
Cho hình lập phương \(ABCD.A'B'C'D'\).
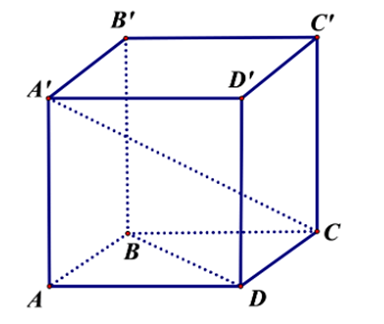
Khẳng định nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì \(ABCD.A'B'C'D'\) là hình lập phương nên \(AD = B'C'\) và \(AD\,{\rm{//}}\,B'C'\).
Từ đó suy ra \(\overrightarrow {AD} = \overrightarrow {B'C'} \).
Câu 8:
Hàm số \(y = f\left( x \right) = 2{x^3} - 9{x^2} - 24x + 1\) nghịch biến trên khoảng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có \(f'\left( x \right) = 6{x^2} - 18x - 24\); \(f'\left( x \right) = 0 \Leftrightarrow x = - 1\) hoặc \(x = 4\).
Bảng biến thiên của hàm số như sau:
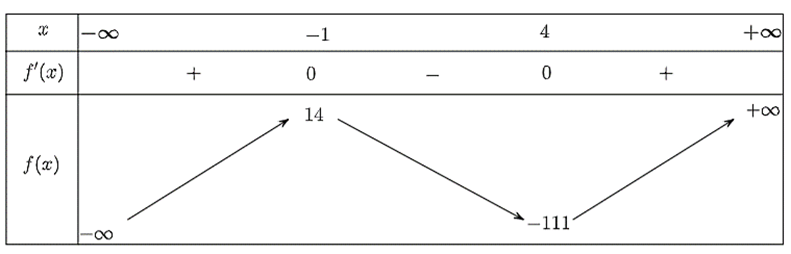
Căn cứ vào bảng biến thiên, ta thấy hàm số đã cho nghịch biến trên khoảng \(\left( { - 1;\,4} \right)\).
Câu 9:
Giá trị nhỏ nhất của hàm số \(y = \sqrt {7 - 6x} \) trên đoạn \(\left[ { - 1;\,1} \right]\) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \(y' = \frac{{ - 3x}}{{\sqrt {7 - 6x} }}\). Khi đó, trên khoảng \(\left( { - 1;\,1} \right)\), \(y' = 0\) khi \(x = 0\).
\(y\left( { - 1} \right) = \sqrt {13} ;\,\,y\left( 0 \right) = \sqrt 7 ;\,\,y\left( 1 \right) = 1\).
Từ đó suy ra \(\mathop {\min }\limits_{\left[ { - 1;\,1} \right]} y = y\left( 1 \right) = 1\).
Câu 10:
Quan sát bảng biến thiên dưới đây và cho biết bảng biến thiên đó là của hàm số nào?
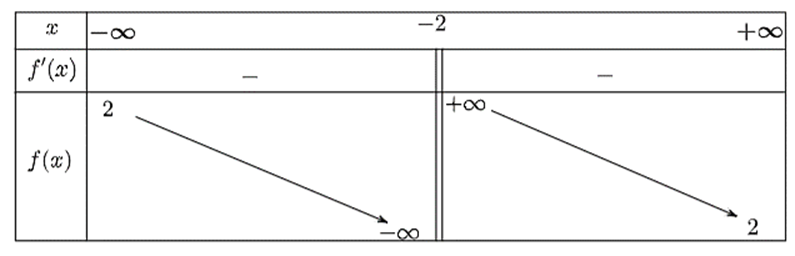
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Từ bảng biến thiên, ta thấy đồ thị hàm số có tiệm cận đứng là \(x = - 2\) và tiệm cận ngang là \(y = 2\) nên ta loại phương án C và D.
Mặt khác, hàm số đã cho nghịch biến trên các khoảng xác định của nó.
Xét hàm số \(y = \frac{{2x - 3}}{{x + 2}}\), ta có \(y' = \frac{7}{{{{\left( {x + 2} \right)}^2}}} > 0\) nên hàm số đồng biến trên các khoảng xác định của nó, do đó ta loại phương án B.
Xét hàm số \(y = \frac{{2x + 5}}{{x + 2}}\), ta có \(y' = \frac{{ - 1}}{{{{\left( {x + 2} \right)}^2}}} < 0\) nên hàm số nghịch biến trên các khoảng xác định của nó, do đó ta chọn phương án A.
Câu 11:
Xác định \(a,\,b,\,c\) để hàm số \(y = \frac{{ax - 1}}{{bx + c}}\) có đồ thị như hình vẽ dưới đây.
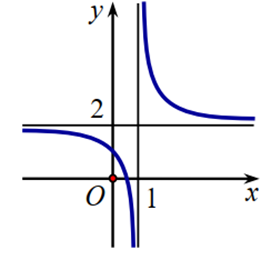
Chọn đáp án đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Từ hình vẽ đã cho, ta thấy đồ thị hàm số có tiệm cận đứng là \(x = 1\) và tiệm cận ngang là \(y = 2\). Khi đó, \(\frac{{ - c}}{b} = 1\) và \(\frac{a}{b} = 2\), tức là \(b = - c\) và \(b = \frac{a}{2}\), suy ra \(c = \frac{{ - a}}{2}\). Vậy trong các phương án đã cho, chỉ có phương án A thỏa mãn.
Câu 12:
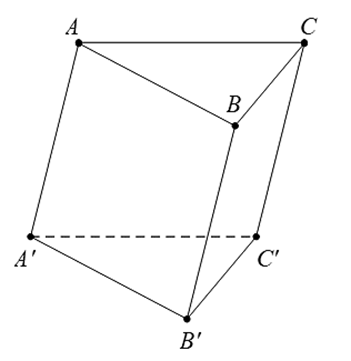
Góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {A'C'} \) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì \(ABC.A'B'C'\) là hình lăng trụ nên \(\overrightarrow {BC} = \overrightarrow {B'C'} \).
Do đó, \(\left( {\overrightarrow {BC} ,\,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {B'C'} ,\,\overrightarrow {A'C'} } \right) = 180^\circ - \widehat {B'C'A'}\).
Mà tam giác \(A'B'C'\) đều nên \(\widehat {B'C'A'} = 60^\circ \). Vậy \(\left( {\overrightarrow {BC} ,\,\overrightarrow {A'C'} } \right) = 120^\circ \).
Câu 13:
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\) và có bảng biến thiên như sau:
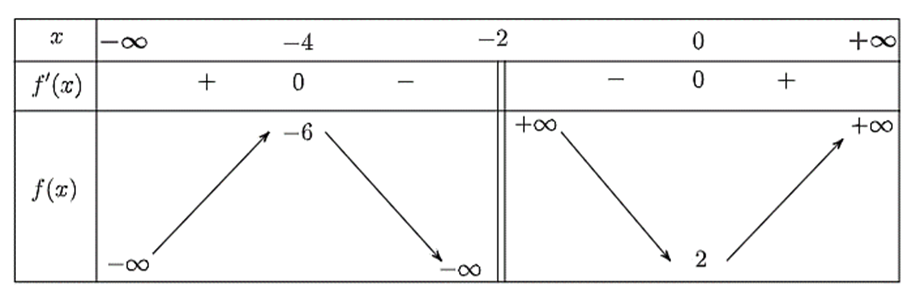
a) Hàm số \(y = f\left( x \right)\) đồng biến trên mỗi khoảng \[\left( { - \infty ; - 4} \right)\] và \(\left( {0;\, + \infty } \right)\).
b) Giá trị cực tiểu của hàm số đã cho là \({y_{CT}} = - 6\).
c) Hàm số \(y = f\left( x \right)\) có giá trị lớn nhất bằng \(2\) và giá trị nhỏ nhất bằng \( - 6\).
d) Công thức xác định hàm số là \(y = \frac{{{x^2} + 2x + 4}}{{x + 2}}\).
 Xem đáp án
Xem đáp án
. a) Đ, b) S, c) S, d) Đ.
Hướng dẫn giải
– Từ bảng biến thiên, ta thấy \(f'\left( x \right) > 0\) với mọi \(x \in \left( { - \infty ; - 4} \right) \cup \left( {0;\, + \infty } \right)\), do đó hàm số \(y = f\left( x \right)\) đồng biến trên mỗi khoảng \[\left( { - \infty ; - 4} \right)\] và \(\left( {0;\, + \infty } \right)\), vậy ý a) đúng.
– Hàm số đạt cực đại tại \(x = - 4\), ; hàm số đạt cực tiểu tại \(x = 0\), \({y_{CT}} = 2\), do đó ý b) sai.
– Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\) nên ý c) sai.
– Xét hàm số \(y = \frac{{{x^2} + 2x + 4}}{{x + 2}}\), ta có:
+ Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).
+ Có \(y' = \frac{{{x^2} + 4x}}{{{{\left( {x + 2} \right)}^2}}}\); \(y' = 0\) khi \(x = - 4\) hoặc \(x = 0\).
+ Trên các khoảng \[\left( { - \infty ; - 4} \right)\] và \(\left( {0;\, + \infty } \right)\), \(y' > 0\).
Trên các khoảng \(\left( { - 4; - 2} \right)\) và \(\left( { - 2;0} \right)\), \(y' < 0\).
+ Hàm số đạt cực đại tại \(x = - 4\), ; hàm số đạt cực tiểu tại \(x = 0\), \({y_{CT}} = 2\).
+ Đường thẳng \(x = - 2\) là tiệm cận đứng của đồ thị hàm số.
Vậy bảng biến thiên đã cho là bảng biến thiên của hàm số \(y = \frac{{{x^2} + 2x + 4}}{{x + 2}}\) nên ý d) đúng.
Câu 14:
Cho hàm số \(y = \frac{{{x^2} - 2x - 3}}{{x - 2}}\).
a) Hàm số đã cho đồng biến trên mỗi khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
b) Hàm số đã cho có 2 cực trị.
c) Đồ thị hàm số nhận điểm \(I\left( {2;2} \right)\) là tâm đối xứng.
d) Có 5 điểm thuộc đồ thị hàm số có tọa độ nguyên.
 Xem đáp án
Xem đáp án
a) Đ, b) S, c) Đ, d) S.
Hướng dẫn giải
Xét hàm số \(y = \frac{{{x^2} - 2x - 3}}{{x - 2}} = x - \frac{3}{{x - 2}}\).
– Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ 2 \right\}\).
– Ta có \(y' = 1 + \frac{3}{{{{\left( {x - 2} \right)}^2}}}\); \(y' > 0\) với mọi \(x \ne 2\).
– Hàm số đồng biến trên từng khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\). Do đó, ý a) đúng.
– Hàm số không có cực trị. Do đó, ý b) sai.
– Tiệm cận: \(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \left( {x - \frac{3}{{x - 2}}} \right) = + \infty ;\,\,\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \left( {x - \frac{3}{{x - 2}}} \right) = - \infty \);
\(\mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( { - \frac{3}{{x - 2}}} \right) = 0;\,\,\mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( { - \frac{3}{{x - 2}}} \right) = 0\).
Do đó, đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = 2\) và tiệm cận xiên là đường thẳng \(y = x\). Vậy tâm đối xứng của đồ thị hàm số là giao điểm \(I\left( {2;\,2} \right)\) của hai đường tiệm cận nên ý c) đúng.
– Với \(x \in \mathbb{Z}\backslash \left\{ 2 \right\}\) thì \(y \in \mathbb{Z}\) khi và chỉ khi \(\frac{3}{{x - 2}} \in \mathbb{Z}\), tức là \(x - 2 \in U\left( 3 \right) = \left\{ { \pm 1;\, \pm 3} \right\}\).
Ta có:
|
\(x - 2\) |
\( - 3\) |
\( - 1\) |
\(1\) |
\(3\) |
|
\(x\) |
\( - 1\) |
\(1\) |
\(3\) |
\(5\) |
|
\(y = x - \frac{3}{{x - 2}}\) |
\(0\) |
\(4\) |
\(0\) |
\(4\) |
Vậy có 4 điểm thuộc đồ thị hàm số có tọa độ nguyên nên ý d) sai.
Câu 15:
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Khi đó:
a) \(\overrightarrow {A'D} = \overrightarrow {BC'} \).
b) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {DA} \).
c) \(\overrightarrow {C'A} = \overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} \).
d) Góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {A'B'} \) bằng \(45^\circ \).
 Xem đáp án
Xem đáp án
. a) S, b) S, c) Đ, d) S.
Hướng dẫn giải
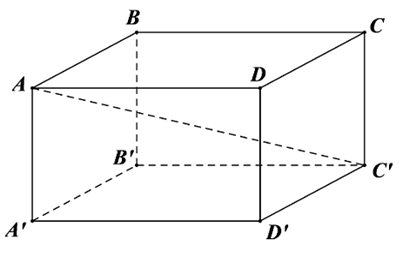
– Vì \(ABCD.A'B'C'D'\) là hình hộp chữ nhật nên \(A'DCB'\) là hình bình hành.
Do đó, \(\overrightarrow {A'D} = \overrightarrow {B'C} \).
Mà hai vectơ \(\overrightarrow {B'C} \) và \(\overrightarrow {BC'} \) không cùng phương nên hai vectơ \(\overrightarrow {A'D} \) và \(\overrightarrow {BC'} \) cũng không cùng phương. Vậy ý a) sai.
– Theo quy tắc ba điểm, ta có \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \ne \overrightarrow {DA} \) nên ý b) sai.
– Do \(ABCD.A'B'C'D'\) là hình hộp chữ nhật nên ta có \(\overrightarrow {A'A} = \overrightarrow {C'C} \).
Áp dụng quy tắc hình hộp cho hình hộp chữ nhật \(ABCD.A'B'C'D'\), ta có:
\(\overrightarrow {C'A} = \overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {C'C} = \overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} \). Vậy ý c) đúng.
– Ta có \(\overrightarrow {AD} = \overrightarrow {A'D'} \) nên \(\left( {\overrightarrow {AD} ,\,\overrightarrow {A'B'} } \right) = \left( {\overrightarrow {A'D'} ,\,\overrightarrow {A'B'} } \right) = \widehat {B'A'D'} = 90^\circ \). Vậy ý d) sai.
Câu 16:
Cho hình chóp tứ giác đều \(S.ABCD\) có độ dài tất cả các cạnh đều bằng \(a\). Đáy \(ABCD\) có tâm là \(O\). Khi đó:
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 4\overrightarrow {SO} \).
b) \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
c) \(\left( {\overrightarrow {SA} ,\,\overrightarrow {AC} } \right) = 45^\circ \).
d) \(\overrightarrow {SA} \cdot \overrightarrow {AC} = - {a^2}\).
 Xem đáp án
Xem đáp án
a) S, b) Đ, c) S, d) Đ.
Hướng dẫn giải
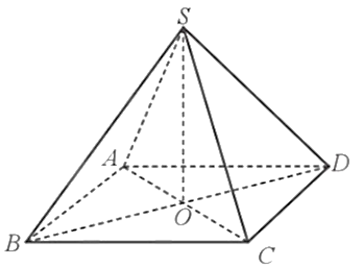
Vì \(S.ABCD\) là hình chóp tứ giác đều nên đáy \(ABCD\) là hình vuông.
Suy ra tâm \(O\) là trung điểm của các đường chéo \(AC\) và \(BD\).
Do đó, \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) và \(\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \).
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \) nên ý a) sai.
Với điểm \(S\), ta có: \(\left\{ \begin{array}{l}\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \\\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \end{array} \right.\). Suy ra \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \) nên ý b) đúng.
Tứ giác \(ABCD\) là hình vuông có độ dài mỗi cạnh là \(a\) nên độ dài đường chéo \(AC\) là \(a\sqrt 2 \). Tam giác \(SAC\) có \(SA = SC = a\) và \(AC = a\sqrt 2 \) nên tam giác \(SAC\) vuông cân tại \(S\), suy ra \(\widehat {SAC} = 45^\circ \). Do đó, \(\left( {\overrightarrow {SC} ,\,\overrightarrow {AC} } \right) = 180^\circ - \widehat {SAC} = 180^\circ - 45^\circ = 135^\circ \).
Suy ra \(\overrightarrow {SA} \cdot \overrightarrow {AC} = \left| {\overrightarrow {SA} } \right| \cdot \left| {\overrightarrow {AC} } \right| \cdot \cos 135^\circ = a \cdot a\sqrt 2 \cdot \left( { - \frac{{\sqrt 2 }}{2}} \right) = - {a^2}\).
Vậy ý c) sai và ý d) đúng.
Câu 17:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ dưới đây.
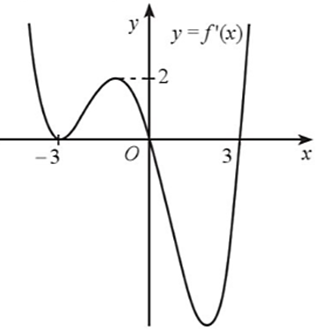
Xét hàm số \(g\left( x \right) = f\left( x \right) - x\). Hàm số \(g\left( x \right)\) có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Do hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) nên hàm số \(y = g\left( x \right)\) cũng xác định trên \(\mathbb{R}\).
Ta có \(g'\left( x \right) = f'\left( x \right) - 1\); \(g'\left( x \right) = 0\) khi \(f'\left( x \right) = 1\).
Số nghiệm của phương trình \(g'\left( x \right) = 0\) là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = 1\).
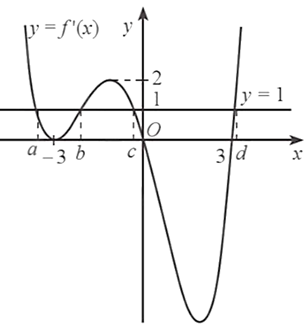
Căn cứ vào đồ thị hàm số, ta thấy phương trình \(f'\left( x \right) = 1\) hay \(g'\left( x \right) = 0\) có 4 nghiệm phân biệt. Gọi 4 nghiệm đó theo thứ tự từ bé đến lớn là \(a,\,b,\,c,\,d\).
Dựa vào vị trí của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = 1\), ta có bảng xét dấu \(g'\left( x \right)\) như sau:

Vậy hàm số \(g\left( x \right) = f\left( x \right) - x\) có 4 điểm cực trị.
Đáp số: 4.
Câu 18:
Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\) với \(m > 1\). Với giá trị nào của tham số \(m\) thì hàm số đã cho có giá trị lớn nhất trên đoạn \(\left[ {1;\,4} \right]\) bằng \(3\)?
 Xem đáp án
Xem đáp án
Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có \(y' = \frac{{1 - m}}{{{{\left( {x + 1} \right)}^2}}}\).
Vì \(m > 1\) nên \(1 - m < 0\), suy ra \(y' = \frac{{1 - m}}{{{{\left( {x + 1} \right)}^2}}} < 0\) với mọi \(x \ne - 1\).
Do đó, hàm số đã cho nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Khi đó, \(\mathop {\max }\limits_{\left[ {1;\,\,4} \right]} y = y\left( 1 \right) = \frac{{1 + m}}{2}\).
Theo đề ra, ta có \(\frac{{1 + m}}{2} = 3 \Leftrightarrow m = 5\).
Đáp số: 5.
Câu 19:
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng có độ dài bằng \(1\) và góc giữa hai vectơ đó bằng \(45^\circ \). Giá trị của tích vô hướng \(\left( {\overrightarrow a + 3\overrightarrow b } \right) \cdot \left( {\overrightarrow a - 2\overrightarrow b } \right)\) bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
 Xem đáp án
Xem đáp án
Ta có: \(\left( {\overrightarrow a + 3\overrightarrow b } \right) \cdot \left( {\overrightarrow a - 2\overrightarrow b } \right)\)
\( = {\overrightarrow a ^2} - 6{\overrightarrow b ^2} + \overrightarrow a \cdot \overrightarrow b \)
\( = {1^2} - 6 \cdot {1^2} + 1 \cdot 1 \cdot \cos 45^\circ \)
\[ = - 5 + \frac{{\sqrt 2 }}{2} \approx - 4,3\].
Đáp số: \( - 4,3\).
Câu 20:
Ngân có một tấm giấy màu có dạng nửa hình tròn bán kính 8 cm. Ngân cần cắt từ tấm giấy màu này ra một tấm giấy hình chữ nhật có một cạnh thuộc đường kính của nửa hình tròn (xem hình dưới) sao cho diện tích của tấm bìa được cắt ra là lớn nhất. Giá trị lớn nhất của diện tích tấm bìa đó là bao nhiêu centimét vuông?
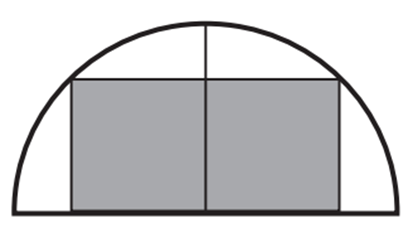
 Xem đáp án
Xem đáp án
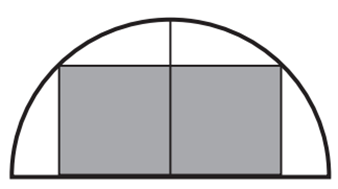
Gọi \(x\,\,\left( {{\rm{cm}}} \right)\) là độ dài một cạnh của tấm giấy hình chữ nhật được cắt ra (cạnh thuộc đường kính) và \(y\,\,\left( {{\rm{cm}}} \right)\) là độ dài cạnh còn lại \((0 < x < 16,\,\,0 < y < 8)\). Ta có:
\({\left( {\frac{x}{2}} \right)^2} + {y^2} = {8^2} \Leftrightarrow {y^2} = \frac{1}{4}\left( {256 - {x^2}} \right) \Leftrightarrow y = \frac{1}{2}\sqrt {256 - {x^2}} \).
Diện tích của tấm giấy hình chữ nhật đó là:
\(S = xy = x \cdot \frac{1}{2}\sqrt {256 - {x^2}} = \frac{1}{2}\sqrt {{x^2}\left( {256 - {x^2}} \right)} \) (cm2).
Đặt \(f\left( x \right) = {x^2}\left( {256 - {x^2}} \right)\) với \(0 < x < 16\), có \(f'\left( x \right) = 512x - 4{x^3}\) nên \(f'\left( x \right) = 0\) khi \(x = 8\sqrt 2 \).
Vậy giá trị lớn nhất của \(S\) bằng \(\frac{1}{2}\sqrt {f\left( {8\sqrt 2 } \right)} = 64\,\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Đáp số: \(64\).
Câu 21:
Độ lớn của các lực căng trên mỗi sợi dây cáp trong hình dưới đây bằng bao nhiêu Newton? Biết rằng khối lượng xe là 1 500 kg, gia tốc là 9,8 m/s2, khung nâng có khối lượng 300 kg và có dạng hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình chữ nhật tâm \(O\), \(AB = 8\) m, \(BC = 12\) m, \(SC = 12\) m và \(SO\) vuông góc với \(\left( {ABCD} \right)\). Làm tròn kết quả đến hàng đơn vị của Newton.
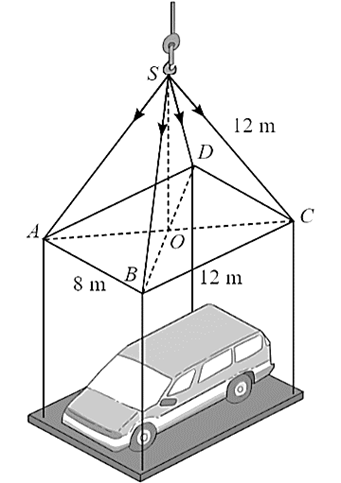
 Xem đáp án
Xem đáp án
Ta có \(AC = BD = \sqrt {{8^2} + {{12}^2}} = 4\sqrt {13} \), \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{{12}^2} - {{\left( {2\sqrt {13} } \right)}^2}} = 2\sqrt {23} \),
\(\sin \widehat {SCO} = \frac{{SO}}{{SC}} = \frac{{2\sqrt {23} }}{{12}} = \frac{{\sqrt {23} }}{6}\).
Gọi \(P\) là độ lớn của trọng lực xe và khung sắt nâng.
Ta có \(P = \left( {1\,500 + 300} \right) \cdot 9,8 = 17\,640\) (N).
Gọi \(F\) là độ lớn của lực căng trên mỗi sợi cáp.
Ta chứng minh được \(F\sin \widehat {SCO} = \frac{P}{4}\), suy ra \(F = \frac{P}{{4\sin \widehat {SCO}}} = \frac{{17\,640}}{{4 \cdot \frac{{\sqrt {23} }}{6}}} \approx 5\,517\) (N).
Đáp số: \(5\,517\).
