Đề thi giữa kì 1 Toán 12 Chân Trời Sáng Tạo có đáp án - Đề 07
-
141 lượt thi
-
22 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số 
có đồ thị là đường cong như hình dưới đây.
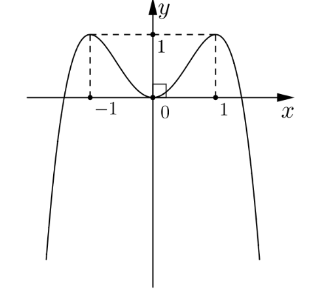
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Xem đáp án
Đáp án đúng là: A
Dựa vào đồ thị hàm số, ta thấy hàm số đã cho đồng biến trên các khoảng 
và 
; nghịch biến trên các khoảng 
và 
.
Câu 2:
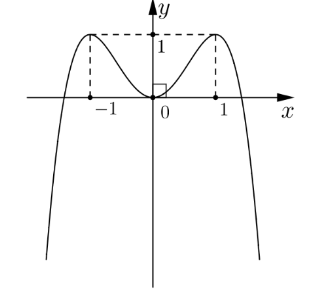
Cho hàm số 
có đồ thị là đường cong như hình dưới đây.
Xem đáp án
Đáp án đúng là: C
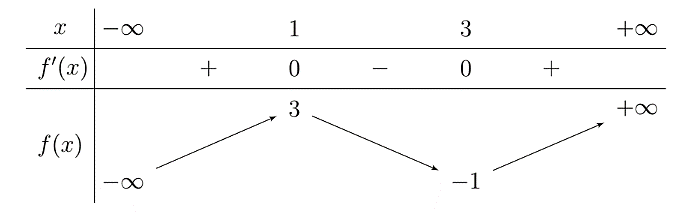
Từ bảng biến thiên, ta thấy hàm số đã cho đạt cực đại tại 
và 
. Vậy hàm số đã cho có hai điểm cực đại.
Câu 3:
Cho hàm số 
có bảng biến thiên trên 
như sau:
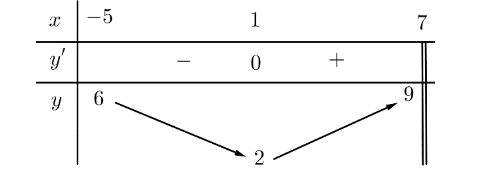
Mệnh đề nào dưới đây là đúng?
Xem đáp án
Đáp án đúng là: B
Dựa vào bảng biến thiên ta có: 
và hàm số không có giá trị lớn nhất trên nửa khoảng 
.
Câu 4:
Cho hàm số 
có đồ thị như hình vẽ dưới đây.
Đồ thị hàm số đã cho có tiệm cận đứng và tiệm cận ngang lần lượt là các đường thẳng:
Xem đáp án
Đáp án đúng là: D
Dựa vào hình vẽ, ta thấy đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng 
và tiệm cận ngang là đường thẳng 
.
Câu 5:
. Vectơ 
bằng vectơ nào dưới đây? Xem đáp án
Đáp án đúng là: D
Theo quy tắc hình hộp, ta có 
.
Câu 7:
, cho vectơ 
và điểm 
. Biết 
. Tọa độ của điểm là: Xem đáp án
Đáp án đúng là: A
Vì 
, mà 
nên 
.
Suy ra tọa độ của điểm 
là 
.
Câu 8:
. Khẳng định nào sau đây là đúng? Xem đáp án
Đáp án đúng là: B
TXĐ của hàm số là \(\mathbb{R}\).
Ta có: \(y' = - 3{x^2} + 6x - 6 = - 3\left( {{x^2} - 2x + 1} \right) - 3 = - 3{\left( {x - 1} \right)^2} - 3 < 0\,\,\forall x \in \mathbb{R}\).
Vậy hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\) và hàm số không có cực trị.
Câu 9:
trên đoạn 
bằng Xem đáp án
Đáp án đúng là: D
Tập xác định của hàm số là 
.
Ta có: 
.
Trên khoảng 
, 
hoặc 
.
.
Vậy 
.
Câu 10:
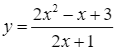là đường thẳng: Xem đáp án
Đáp án đúng là: A
Tập xác định của hàm số là 
.
Ta có: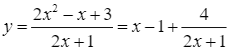 
.
; 
.
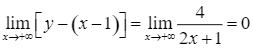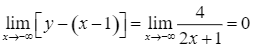Vậy đường thẳng 
là tiệm cận xiên của đồ thị hàm số đã cho.
Câu 11:
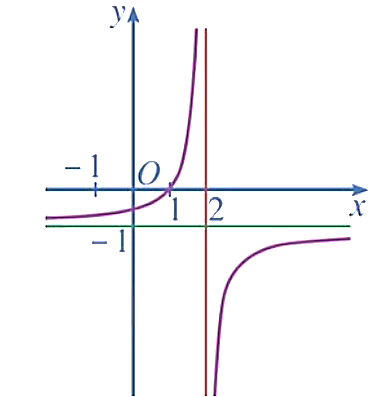
Đường cong trong hình dưới đây là đồ thị của hàm số nào trong bốn hàm số ở các phương án A, B, C, D.
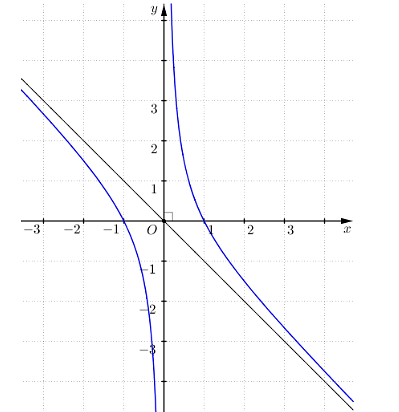
Xem đáp án
Đáp án đúng là: A
Quan sát hình vẽ, ta thấy đây là dáng của đồ thị hàm số phân thức bậc hai trên bậc nhất, do đó ta loại phương án B và D.
Mặt khác, ta thấy đường thẳng 
(trục tung) là tiệm cận đứng của đồ thị hàm số đã cho, do vậy ta chọn phương án A.
Câu 12:
có cạnh bằng 
. Góc giữa hai vectơ 
và 
bằng: Xem đáp án
Đáp án đúng là: C
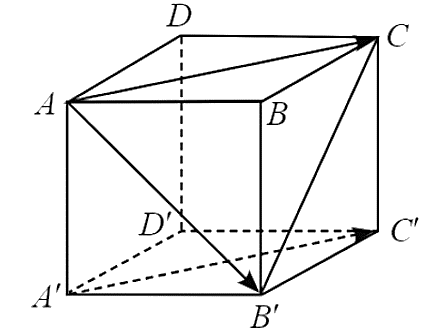
Ta có 
, suy ra 
.
Lại có 
nên tam giác 
là tam giác đều, suy ra 
.
Vậy 
.
Câu 13:
Cho hàm số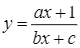 
(
là các tham số) có bảng biến thiên như sau:
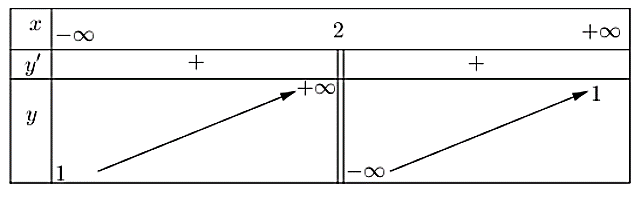
a) Hàm số đã cho đồng biến trên các khoảng 
và 
.
b) Hàm số đã cho có 
điểm cực trị.
c) Trên khoảng , giá trị lớn nhất của hàm số đã cho bằng 
.
d) Giá trị của biểu thức 
bằng 
.
Xem đáp án
a) Đ, b) S, c) S, d) Đ.
Hướng dẫn giải
Quan sát bảng biến thiên, ta thấy:
– Hàm số đã cho đồng biến trên các khoảng 
và 
. Vậy ý a) đúng.
– Hàm số đã cho không có cực trị. Vậy ý b) sai.
– Trên khoảng , ta có 
, tuy nhiên không tồn tại giá trị của 
để 
nên hàm số đã cho không có giá trị lớn nhất trên khoảng này. Do đó, ý c) sai.
– Đồ thị hàm số có tiệm cận đứng là đường thẳng 
và tiệm cận ngang là đường thẳng nên ta có hệ sau: 
.
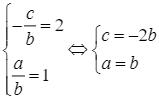Khi đó, 
.
Vậy ý d) đúng.
Câu 14:
Cho hàm số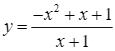 
có đồ thị 
.
a) Hàm số đã cho nghịch biến trên các khoảng 
và 
.
b) Đồ thị có hai điểm cực trị nằm ở hai phía đối với trục tung.
c) Đồ thị có đường tiệm cận đứng là 
; đường tiệm cận xiên là 
.
d) Đồ thị nhận điểm 
làm tâm đối xứng.
Xem đáp án
a) Đ, b) S, c) Đ, d) Đ.
Xét hàm số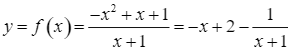 
.
– Tập xác định của hàm số là 
.
– Ta có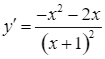 
; 
khi 
hoặc 
.
Bảng biến thiên của hàm số như sau:
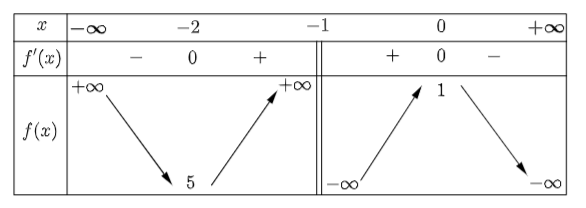
– Hàm số đã cho nghịch biến trên từng khoảng 
và 
. Do đó, ý a) đúng.
– Hàm số đã cho đạt cực đại tại , 
; đạt cực tiểu tại , 
.
Khi đó, điểm cực đại của đồ thị 
là 
thuộc trục tung. Vậy hai điểm cực trị của đồ thị không thể nằm ở hai phía đối với trục tung. Do đó, ý b) sai.
– Tiệm cận:
+) Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng 
.
+) Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng 
.
Vậy ý c) đúng.
– Đồ thị nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.
Với thì 
.
Vậy điểm 
là tâm đối xứng của đồ thị .
Do đó, ý d) đúng.
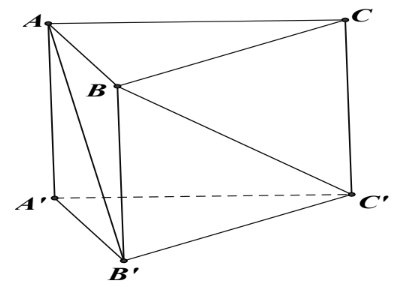
Câu 15:
Cho hình lăng trụ tam giác đều 
có 
, 
.
a) 
.
b) 
.
c)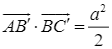 
.
d) 
.
Xem đáp án
a) Đ, b) Đ, c) S, d) Đ.
Hướng dẫn giải
– Vì 
là lăng trụ tam giác đều nên 
.
Theo quy tắc ba điểm ta có: 
. Vậy ý a) đúng.
Xem đáp án
a) Đ, b) S, c) Đ, d) Đ.
Hướng dẫn giải
– Ta có 
. Suy ra 
.
Do đó, ý a) đúng.
– Ta có: 
. Do đó, ý b) sai.
– Điểm 
có hoành độ 
, tung độ 
và cao độ 
nên điểm 
nằm trong mặt phẳng 
. Do đó, ý c) đúng.
– Gọi tọa độ điểm 
là 
, ta có 
.
Khi đó, 
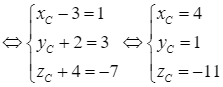. Vậy 
.
Do đó, ý d) đúng.
Câu 17:
đạt cực đại tại 
và đạt cực tiểu tại 
. Giá trị của biểu thức 
là bao nhiêu?
Câu 18:
, trong đó 
tính bằng mét, 
tính bằng giây. Gia tốc lớn nhất của chất điểm bằng bao nhiêu mét trên giây (làm tròn kết quả đến hàng phần mười)? Xem đáp án
Vận tốc tức thời của chất điểm là 
.
Gia tốc tức thời của chất điểm là 
.
Ta có: 
với mọi 
.
Tức là 
. Vậy 
với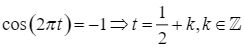 
.
Vậy gia tốc lớn nhất của chất điểm bằng khoảng 
m/s2.
Đáp số: .
Câu 19:
. Gọi 
lần lượt là trọng tâm của các tam giác 
, 
. Khi đó ta có 
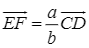(với 
là phân số tối giản và 
). Giá trị của biểu thức 
bằng bao nhiêu? Xem đáp án
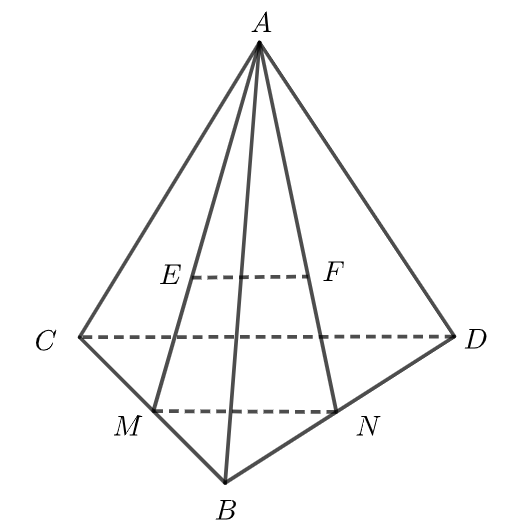
Gọi 
lần lượt là trung điểm của 
.
Khi đó, ta có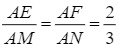 
(tính chất trọng tâm). Suy ra 
và 
.
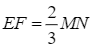Vì hai vectơ 
và 
cùng hướng nên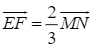 
. (1)
Lại có 
là đường trung bình của tam giác 
nên 
và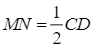 
.
Vì hai vectơ và 
cùng hướng nên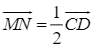 
. (2)
Từ (1) và (2) suy ra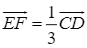 
. Do đó, 
. Vậy 
.
Đáp số: 
.
Câu 20:
, cho ba điểm 
, 
. Điểm 
là đỉnh thứ tư của hình bình hành 
. Giá trị của biểu thức 
bằng bao nhiêu? Xem đáp án
Ta có 
.
Tứ giác 
là hình bình hành 
.
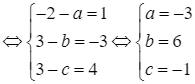Suy ra 
.
Đáp số: 
.
Câu 21:
Hai con tàu 
và 
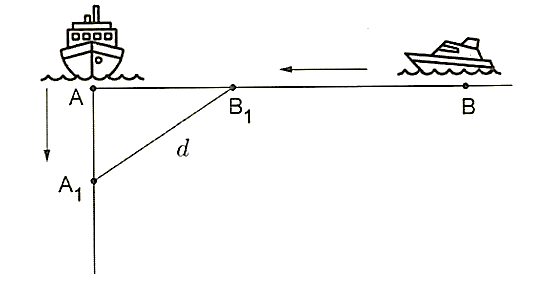
đang ở cùng một vĩ tuyến và cách nhau 5 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu chạy về hướng Nam với vận tốc 6 hải lí/giờ, còn tàu chạy về vị trí hiện tại của tàu với vận tốc 7 hải lí/giờ (tham khảo hình vẽ). Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần mười)?
Xem đáp án
Tại thời điểm 
(giờ) sau khi xuất phát, khoảng cách giữa hai tàu là 
. Khi đó, tàu 
đang ở vị trí 
và tàu 
đang ở vị trí 
như hình vẽ trên.
Ta có: 
.
Suy ra 
.
Xét hàm số 
với 
.
Ta có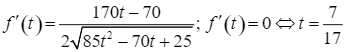 
.
Bảng biến thiên của hàm số 
trên khoảng 
như sau:
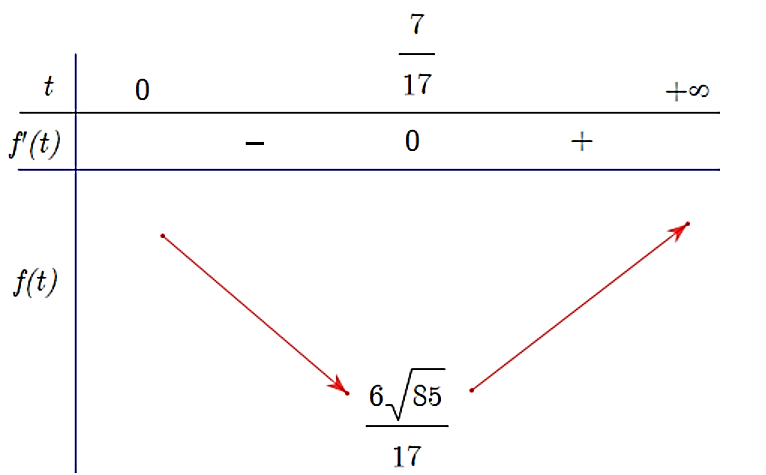
Từ bảng biến thiên, ta có: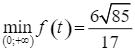 
tại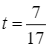 
.
Vậy sau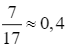 
giờ thì khoảng cách giữa hai tàu là bé nhất.
Đáp số: 
.
Câu 22:
Một chất điểm ở vị trí đỉnh 
của hình lập phương 
. Chất điểm chịu tác động bởi ba lực 
lần lượt cùng hướng với 
như hình vẽ.
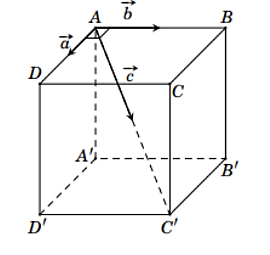
Độ lớn của các lực tương ứng là 10 N, 10 N và 20 N. Độ lớn hợp lực của các lực bằng bao nhiêu Newton (làm tròn kết quả đến hàng phần mười)?
Xem đáp án
Từ giả thiết, ta suy ra được:
; 
.
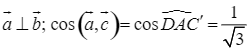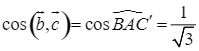Giả sử lực tổng hợp là 
, tức là 
.
Khi đó, 
.
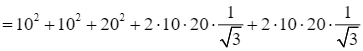
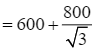Suy ra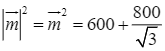 
. Do đó, 
.
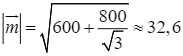Vậy độ lớn hợp lực của các lực 
bằng khoảng 
N.
Đáp số: .