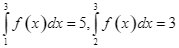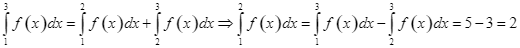Đề thi giữa kì 2 Toán 12 Cánh Diều có đáp án - Đề 10
-
82 lượt thi
-
22 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
là
Xem đáp án
Đáp án đúng là: A
Vì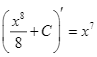 
.
Câu 4:
Cho hàm số 
có đạo hàm liên tục thỏa mãn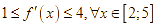 
. Khẳng định nào dưới đây là khẳng định đúng?
Xem đáp án
Đáp án đúng là: A
Ta có 
suy ra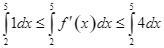 
.
Câu 5:
Cho đồ thị hàm số 
như hình sau. Diện tích hình phẳng (phân tô đậm trong hình) được tính bởi công thức
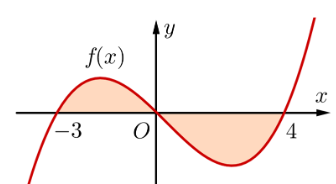
Xem đáp án
Đáp án đúng là: A
.
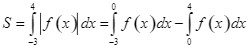
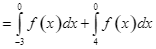Câu 6:
và trục hoành quanh trục hoành bằng Xem đáp án
Đáp án đúng là: A
Phương trình hoành độ giao điểm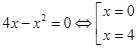 
.
Ta có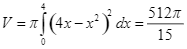 
.
Câu 7:
, cho mặt phẳng 
. Điểm nào dưới đây thuộc 
? Xem đáp án
Đáp án đúng là: D
Ta thấy 
nên 
thuộc 
.
Câu 8:
, cho mặt phẳng 
. Vectơ nào dưới đây là một vectơ pháp tuyến của 
? Xem đáp án
Đáp án đúng là: C
Mặt phẳng 
có một vectơ pháp tuyến là 
.
Câu 9:
, gọi 
là hình chiếu vuông góc của điểm 
lên mặt phẳng 
. Độ dài đoạn thẳng 
là Xem đáp án
Đáp án đúng là: D
Ta có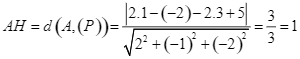 
.
Câu 10:
, mặt phẳng 
có phương trình là Xem đáp án
Đáp án đúng là: A
Mặt phẳng 
có phương trình là 
.
Câu 11:
, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm 
và có một vectơ pháp tuyến 
. Xem đáp án
Đáp án đúng là: A
Phương trình cần tìm là 
hay 
.
Câu 12:
, cho điểm 
. Gọi 
lần lượt là hình chiếu vuông góc của điểm 
trên các trục 
. Viết phương trình mặt phẳng 
. Xem đáp án
Đáp án đúng là: C
lần lượt là hình chiếu của 
trên các trục 
.
Phương trình mặt phẳng 
là 
.
Câu 13:
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số 
và 
.
a) 
là một nguyên hàm của 
.
b) 
.
c) 
.
d)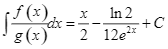 
.
Xem đáp án
a) S, b) Đ, c) S, d) S
a) Ta có 
. Do đó 
không là một nguyên hàm của 
.
b) 
.
c) 
.
d)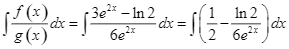 
.
Câu 14:
Cho hàm số 
.
a)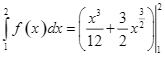 
.
b)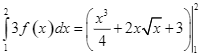 
.
c)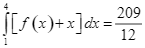 
.
d) Diện tích hình thang cong giới hạn bởi đồ thị hàm số 
, trục hoành và các đường thẳng 
lớn hơn 5.
Xem đáp án
a) S, b) S, c) Đ, d) S
a)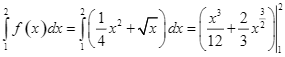 
.
b)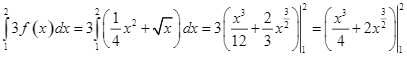 
.
c)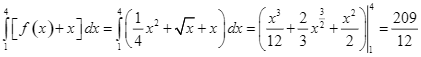 
.
d)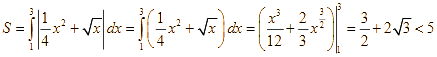 
.
Câu 15:
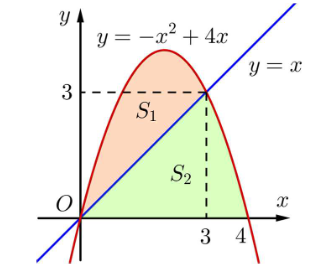
Cho 
lần lượt là diện tích các hình phẳng 
được mô tả trong hình sau:
a)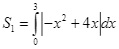 
.
b)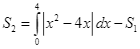 
.
c)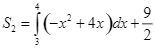 
.
d) Thể tích khối tròn xoay khi quay 
quanh trục 
nhỏ hơn 30.
Xem đáp án
a) S, b) Đ, c) Đ, d) S
a)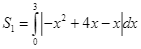 
.
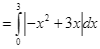b)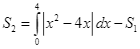 
.
c)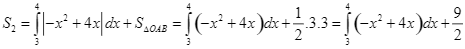 
.
(với 
).
d)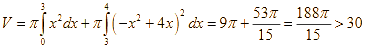 
.
Câu 16:
Trong không gian với hệ tọa độ 
, cho điểm
và mặt phẳng 
.
a) Mặt phẳng có một vectơ pháp tuyến là 
.
b) Điểm không thuộc mặt phẳng .
c) Điểm cách mặt phẳng 
một khoảng bằng 1.
d) Phương trình mặt phẳng 
đi qua 
chứa trục 
có dạng 
. Khi đó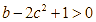 
.
Xem đáp án
a) Đ, b) Đ, c) Đ, d) Đ
a) Mặt phẳng 
có một vectơ pháp tuyến là 
.
b) Thay tọa độ điểm 
vào phương trình mặt phẳng ta được
. Do đó điểm không thuộc mặt phẳng .
c) Mặt phẳng 
có phương trình 
.
Suy ra 
.
d) Có 
và 
.
Có 
.
Phương trình mặt phẳng 
có dạng: 
hay 
.
Suy ra 
. Do đó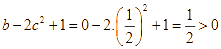 
.
Câu 17:
là họ nguyên hàm của hàm số 
. Giá trị 
bằng bao nhiêu? Xem đáp án
Trả lời: 3
Ta có 
.
Mà 
. Do đó 
.
Suy ra 
.
Câu 18:
là một nguyên hàm của hàm số 
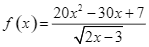trên khoảng 
. Tính 
. Xem đáp án
Trả lời: −8
Có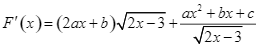 
.
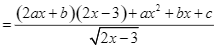
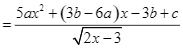Vì 
là một nguyên hàm của hàm số 
nên ta có:
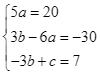
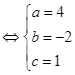. Do đó 
.
Câu 19:
và gia tốc trọng trường là 
(bỏ qua sức cản của không khí). Quãng đường viên đạn đi được từ lúc bắn lên cho tới khi rơi xuống đất là bao nhiêu kilômét? Xem đáp án
Trả lời: 3,92
Vận tốc của viên đạn là 
.
Vì 
nên 
. Do đó 
.
Khi viên đạn đạt độ cao lớn nhất thì viên đạn có vận tốc bằng 0.
Suy ra 
.
Quãng đường viên đạn đi từ mặt đất đến vị trí cao nhất là
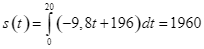(m)
Quãng đường viên đạn đi được từ lúc bắn lên cho tới khi rơi xuống đất là
m 
km.
Câu 20:
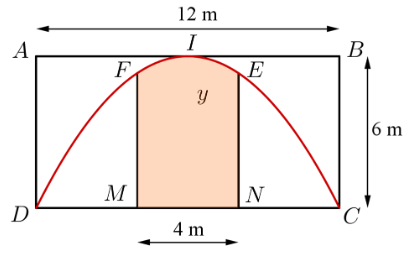
Một công ty quảng cáo muốn làm một bức tranh trang trí hình 
ở chính giữa của một bức tường hình chữ nhật 
có chiều cao 
, chiều dài 
(hình vẽ bên). Cho biết 
là hình chữ nhật có 
, cung 
có hình dạng là một phần của parabol có đỉnh 
là trung điểm của cạnh 
và đi qua 2 điểm 
. Đơn giá làm bức tranh là 900000 đồng/m2. Hỏi công ty đó cần bao nhiêu tiền để làm bức tranh đó (đơn vị: triệu đồng)?
Xem đáp án
Trả lời: 20,8
Chọn hệ trục tọa độ với 
là trung điểm của 
, trục hoành trùng với đường thẳng .
Giả sử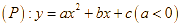 
.
Vì 
đi qua 
.
Do đó ta có hệ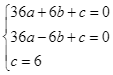 
.
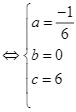Do đó 
.
Diện tích cần làm là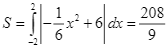 
.
Số tiền cần dùng là:
đồng = 20,8 triệu đồng.
Câu 21:
và 
. Phương trình mặt phẳng 
đi qua gốc tọa độ đồng thời vuông góc 
và 
có dạng 
. Tính 
. Xem đáp án
Trả lời: −4
Có 
. Suy ra 
.
Mặt phẳng 
đi qua gốc tọa độ nên 
.
Do đó 
. Vậy 
.
Câu 22:
, cho hình hộp 
có 
. Chiều cao của hình hộp là 
. Giá trị của 
bằng bao nhiêu? Xem đáp án
Trả lời: 18
Ta có 
.
Mặt phẳng 
đi qua 
và nhận vectơ 
làm vectơ pháp tuyến có dạng
hay 
.
Chiều cao của hình hộp 
chính là 
.
Ta có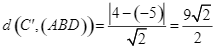 
. Suy ra 
.
Vậy 
.