Bộ 15 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023 (Đề 8)
-
6405 lượt thi
-
39 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ và . Tính góc giữa hai vectơ và .
 Xem đáp án
Xem đáp án
Chọn A
Câu 4:
Cho , với và phân số tối giản. Phát biểu nào sau đây là sai?
 Xem đáp án
Xem đáp án
Chọn C
Đặt
Khi đó: . Khi đó: đáp án C sai.
Đặt
Khi đó: . Khi đó: đáp án C sai.
Câu 5:
Biết F(x) là một nguyên hàm của hàm số thỏa mãn . Hỏi F(3) bằng bao nhiêu ?
 Xem đáp án
Xem đáp án
Chọn B.
Ta có .
Do nên C = 1, từ đó .
Ta có .
Do nên C = 1, từ đó .
Câu 6:
Cho f(x) và g(x) là các hàm số xác định và liên tục trên R. Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Chọn D.
Câu 7:
Biết hàm số f(x) có đạo hàm f'(x) liên tục trên R thỏa mãn và . Tính .
 Xem đáp án
Xem đáp án
Chọn B.
Ta có .
Ta có .
Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm và . Viết phương trình mặt cầu (S) đường kính AB.
 Xem đáp án
Xem đáp án
Chọn D.
Tọa độ trung điểm AB là và .
Suy ra .
Tọa độ trung điểm AB là và .
Suy ra .
Câu 9:
Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây không là phương trình của mặt cầu ?
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
là phương trình một mặt cầu vì
là phương trình một mặt cầu
là phương trình một mặt cầu
không là phương trình một mặt cầu
Ta có:
là phương trình một mặt cầu vì
là phương trình một mặt cầu
là phương trình một mặt cầu
không là phương trình một mặt cầu
Câu 12:
Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng và mặt phẳng , với m là tham số thực .Tìm tất cả các giá trị của tham số để hai mặt phẳng (P) và (Q) song song nhau .
 Xem đáp án
Xem đáp án
Chọn A
Ta có
Ta có
Câu 13:
Cho cấp số cộng có và công sai . Tìm biểu thức số hạng tổng quát của dãy số này.
 Xem đáp án
Xem đáp án
Chọn B
Câu 14:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có các đỉnh và . Gọi là trực tâm của tam giác ABC. Tính a+b+c
 Xem đáp án
Xem đáp án
Chọn D
Ta có : .
Phương trình mặt phẳng .
H là trực tâm
.
Ta có : .
Phương trình mặt phẳng .
H là trực tâm
.
Câu 16:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm và mặt phẳng . Tìm phương trình mặt cầu (S) đi qua ba điểm A, B, C và có tâm thuộc mặt phẳng (P).
 Xem đáp án
Xem đáp án
Chọn D
Gọi là tâm của mặt cầu (S)
Ta có
Gọi là tâm của mặt cầu (S)
Ta có
Câu 19:
Trong không gian với hệ tọa độ Oxyz, tìm phương trình mặt phẳng đi qua 3 điểm .
 Xem đáp án
Xem đáp án
Chọn B
đi qua 3 điểm có VTPT
Pttq .
đi qua 3 điểm có VTPT
Pttq .
Câu 20:
Trong không gian với hệ tọa độ Oxyz, tìm phương trình mặt cầu (S) đi qua hai điểm và có tâm nằm trên trục Oz .
 Xem đáp án
Xem đáp án
Chọn D
Gọi là tâm mặt cầu.
Mặt cầu (S) đi qua hai điểm nên
Bán kính mặt cầu .
Mặt cầu (S) có tâm và có bán kính
.
Gọi là tâm mặt cầu.
Mặt cầu (S) đi qua hai điểm nên
Bán kính mặt cầu .
Mặt cầu (S) có tâm và có bán kính
.
Câu 22:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC biết các đỉnh , và . Gọi G là trọng tâm của tam giác ABC. Gọi H là hình chiếu vuông góc của G lên mặt phẳng (Oxz). Tìm tọa độ điểm H.
 Xem đáp án
Xem đáp án
Chọn C
Tọa độ trọng tâm tam giác ABC là .
Hình chiếu của G lên (Oxz) là .
Tọa độ trọng tâm tam giác ABC là .
Hình chiếu của G lên (Oxz) là .
Câu 23:
Cho hàm số . Tìm một nguyên hàm F(x) của hàm số f(x) biết đồ thị hàm số đi qua điểm .
 Xem đáp án
Xem đáp án
Chọn C
Câu 25:
Cho là một nguyên hàm của hàm số thỏa mãn và là một nguyên hàm của hàm số thỏa mãn . Tìm nghiệm của phương trình .
 Xem đáp án
Xem đáp án
Chọn B
Câu 26:
Cho f(x) và g(x) là hai hàm số liên tục trên . Biết f(x) là hàm số lẻ; g(x) là hàm số chẵn và . Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Chọn B
Chọn B
Ta có . Mặt khác .
Suy ra
Ta có . Mặt khác .
Suy ra
Câu 27:
Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có đỉnh A trùng với gốc tọa độ, và . Gọi M là trung điểm cạnh CC'. Tính thể tích V của khối tứ diện A'BDM.
 Xem đáp án
Xem đáp án
Chọn A
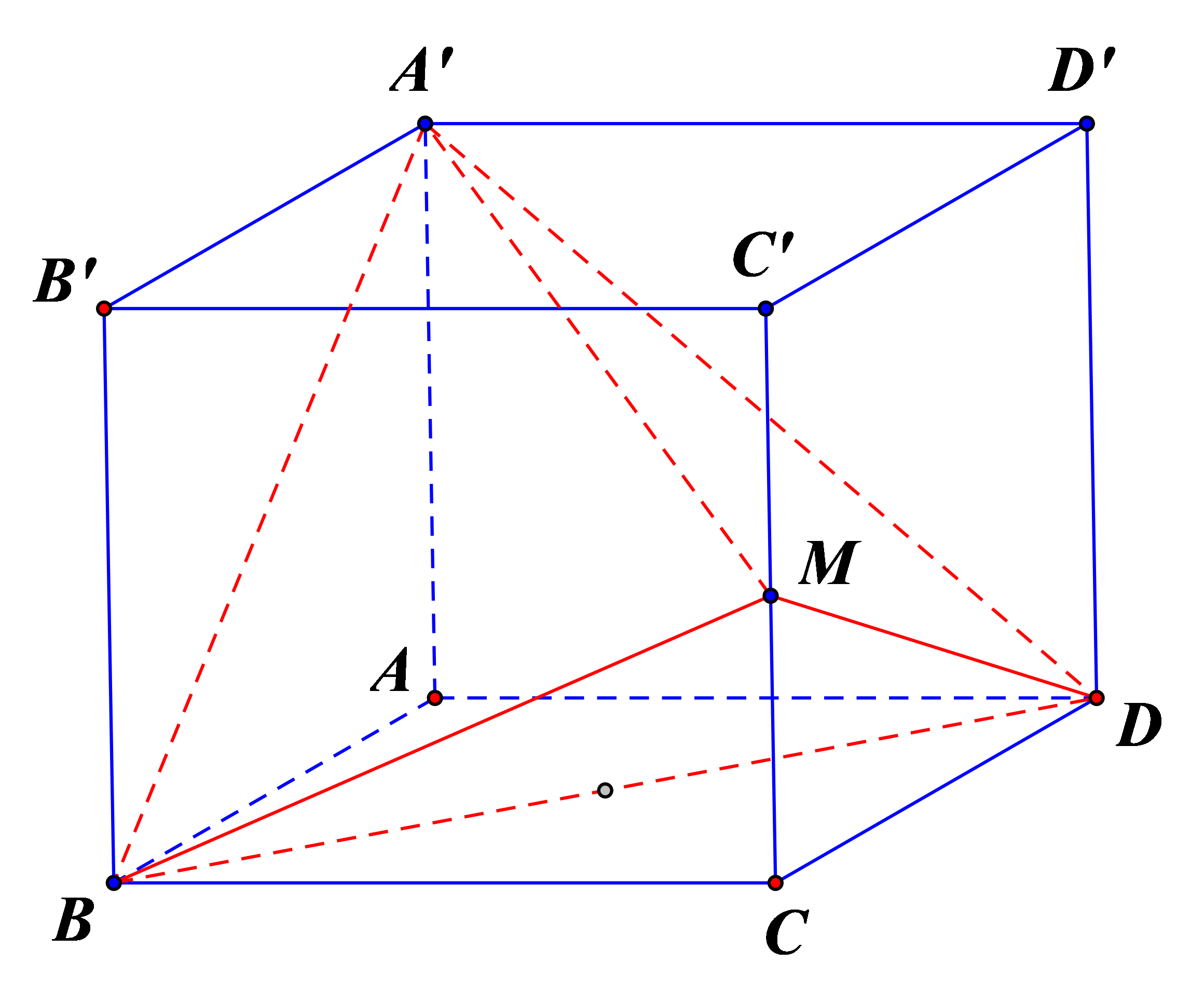
Ta có .
.
Suy ra .

Ta có .
.
Suy ra .
Câu 28:
Cho . Nếu đổi biến số thì kết luận nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn D
Đổi biến số . Khi đó . Do đó
Đổi biến số . Khi đó . Do đó
Câu 30:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và B(3;2;1). Tìm phương trình mặt phẳng đi qua điểm A và cách điểm B một khoảng lớn nhất.
 Xem đáp án
Xem đáp án
Chọn A
Gọi H là hình chiếu của B lên
Khi đó: (không đổi)
Dấu = xảy ra .
Lúc đó đi qua điểm A và nhận làm vtpt nên có pt: .
Gọi H là hình chiếu của B lên
Khi đó: (không đổi)
Dấu = xảy ra .
Lúc đó đi qua điểm A và nhận làm vtpt nên có pt: .
Câu 31:
Trong không gian với hệ toạ độ Oxyz, cho A(2;0;0), B(0;3;1), C(-3;6;4). Gọi Q là điểm nằm trên đoạn BC sao cho . Độ dài đoạn AQ là
 Xem đáp án
Xem đáp án
Chọn A
Q là điểm nằm trên đoạn BC sao cho .
Q là điểm nằm trên đoạn BC sao cho .
Câu 32:
Cho hai hàm số và với và . Tính tích để F(x) là một nguyên hàm của hàm số f(x) trên khoảng .
 Xem đáp án
Xem đáp án
Chọn C
F(x) là một nguyên hàm của hàm số f(x) trên khoảng
Tính
.
Do đó
F(x) là một nguyên hàm của hàm số f(x) trên khoảng
Tính
.
Do đó
.
Câu 33:
Trong không gian với hệ tọa độ cho Oxyz, A(2;3;1), B(1;1;0) và điểm M(a;b;0) sao cho đạt giá trị nhỏ nhất. Khi đó, tính giá trị của biểu thức a+2b
 Xem đáp án
Xem đáp án
Chọn B
Gọi điểm I thỏa mãn .
P đạt giá trị nhỏ nhất nhỏ nhất là hình chiếu của I lên mặt phẳng (Oxy)
.
Gọi điểm I thỏa mãn .
P đạt giá trị nhỏ nhất nhỏ nhất là hình chiếu của I lên mặt phẳng (Oxy)
.
Câu 35:
Cho hàm số f(x) liên tục trên R thỏa mãn . Đặt , tính giá trị biểu thức .
 Xem đáp án
Xem đáp án
Chọn B
Ta có .
Từ đó
Ta có .
Từ đó
Câu 36:
Cho hàm số f(x) liên tục trên R thỏa mãn f(2) = 18 và . Tính .
 Xem đáp án
Xem đáp án
Chọn A
Xét tích phân K: đặt . Đổi cận: ; .
.
Xét tích phân K: đặt . Đổi cận: ; .
.
Câu 37:
Trong không gian Oxyz, cho hình chóp S.ABCD có các đỉnh B(3;0;1), D(1;2;7), đáy ABCD là hình thoi, SA vuông góc với mặt phẳng đáy. Tính tổng biết phương trình mặt (SAC) phẳng có dạng .
 Xem đáp án
Xem đáp án
Chọn A
Do ABCD là hình thoi nên , lại có nên .
Mặt phẳng (SAC) qua trung điểm của BD, nhận làm véctơ pháp tuyến nên .
Do đó .
Do ABCD là hình thoi nên , lại có nên .
Mặt phẳng (SAC) qua trung điểm của BD, nhận làm véctơ pháp tuyến nên .
Do đó .
Câu 38:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm , , . Phương trình mặt phẳng đi qua A và vuông góc với BC là
 Xem đáp án
Xem đáp án
Chọn A
Mặt phẳng đi qua A và vuông góc với BC nhận làm véctơ pháp tuyến
có phương trình dạng: .
Vậy phương trình mặt phẳng (Q) là: .
Mặt phẳng đi qua A và vuông góc với BC nhận làm véctơ pháp tuyến
có phương trình dạng: .
Vậy phương trình mặt phẳng (Q) là: .
Câu 39:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm , . Phương trình mặt phẳng trung trực của AB là
 Xem đáp án
Xem đáp án
Chọn D
Gọi I là trung điềm của .
Ta có: .
Suy ra: có phương trình là .
Gọi I là trung điềm của .
Ta có: .
Suy ra: có phương trình là .
