Bộ 15 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023 (Đề 1)
-
6370 lượt thi
-
39 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 2:
Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Chọn đáp án D
Các nguyên hàm có thể có hằng số khác nhau.
Câu 3:
Khẳng định nào say đây đúng?
 Xem đáp án
Xem đáp án
Theo bảng nguyên hàm của một số hàm số thường gặp: .
Chọn đáp án C
Câu 4:
Cho F(x) là một nguyên hàm của hàm số thỏa mãn , giá trị của F(2) bằng
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 5:
Cho hai hàm số f(x) và g(x) xác định và liên tục trên R. Trong các khẳng định sau, có bao nhiêu khẳng định sai?
(I) .
(II) .
(III) với mọi số thực k.
(IV) .
(I) .
(II) .
(III) với mọi số thực k.
(IV) .
 Xem đáp án
Xem đáp án
Khẳng định (II) và (III) là sai, vì .
Chọn đáp án B
Câu 6:
Cho hàm số và . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án D
Ta có . Từ đó suy ra .
.
Vậy hàm .
.
Vậy hàm .
Câu 9:
Cho f(x) là hàm số liên tục trên và F(x) là một nguyên hàm của f(x). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn D
Câu 10:
Tích phân . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Áp dụng định nghĩa tích phân:
Ta có: .
Ta có: .
Chọn đáp án D
Câu 11:
Cho hai hàm số g(x), f(x) liên tục trên đoạn và số thực k. Trong các khẳng định sau, khẳng định nào sai ?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 12:
Cho hàm số liên tục trên đoạn . Trong các khẳng định sau, khẳng định nào đúng ?
 Xem đáp án
Xem đáp án
Áp dụng tính chất .
Ta có: .
Ta có: .
Chọn đáp án A
Câu 13:
Cho f(x); g(x) là hai hàm số liên tục trên R và các số thực a, b, c. Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Theo tính chất tích phân ta chọn D.
Câu 15:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm và . Tọa độ vectơ là
 Xem đáp án
Xem đáp án
Ta có: .
Chọn D
Câu 17:
Trong không gian Oxyz cho mặt cầu . Tìm tọa độ tâm và bán kính của mặt cầu.
 Xem đáp án
Xem đáp án
Mặt cầu có tâm I (1;2;3), bán kính R = 5.
Chọn A
Câu 18:
Cho mặt phẳng . Vectơ nào là một vectơ pháp tuyến của (P)?
 Xem đáp án
Xem đáp án
Vecto pháp tuyến
Chọn C
Câu 19:
Trong không gian Oxyz, vectơ nào sau đây là một vectơ pháp tuyến của (P). Biết , là cặp vectơ chỉ phương của (P).
 Xem đáp án
Xem đáp án
Ta có (P) có một vectơ pháp tuyến là .
Chọn B
Câu 22:
Cho với và . Giá trị của biểu thức là
 Xem đáp án
Xem đáp án
Đặt .
Theo đề bài ta có:
Đồng nhất hệ số ta được: .
Theo đề bài ta có:
Đồng nhất hệ số ta được: .
Chọn A
Câu 23:
Biết hàm số có , và đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng -3. Hàm số f(x) là
 Xem đáp án
Xem đáp án
Chọn A
Ta có: .
Theo đề bài, ta có: .
Vậy .
Theo đề bài, ta có: .
Vậy .
Câu 29:
Cho với a, b, c là các số nguyên. Giá trị của a + b + c bằng
 Xem đáp án
Xem đáp án
Đặt .
Đổi cận: ; .
Khi đó:
Đổi cận: ; .
Khi đó:
Suy ra .
Chọn A
Câu 32:
Cho Tìm m để 4 điểm A, B, C đồng phẳng.
 Xem đáp án
Xem đáp án
Chọn đáp án D
Ta có: .
A, B, C, D đồng phẳng
A, B, C, D đồng phẳng
Câu 33:
Trong không gian với hệ trục tọa độ Oxyz, tìm tập hợp tất cả các giá trị của tham số m để phương trình là phương trình mặt cầu:
 Xem đáp án
Xem đáp án
Chọn B
Phương trình có dạng với .
Phương trình đã cho là phương trình mặt cầu khi và chỉ khi .
Phương trình đã cho là phương trình mặt cầu khi và chỉ khi .
Câu 34:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): và mặt cầu . Để mặt phẳng (P) tiếp xúc với mặt cầu thì tổng các giá trị của tham số là:
 Xem đáp án
Xem đáp án
Chọn C
Mặt cầu (S) có tâm và bán kính .
Để mặt phẳng (P) tiếp xúc với mặt cầu (S) thì
.
Vậy tổng các giá trị của m là: .
Để mặt phẳng (P) tiếp xúc với mặt cầu (S) thì
.
Vậy tổng các giá trị của m là: .
Câu 35:
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng (P) đi qua điểm và chứa trục Oz là . Tính tỉ số .
 Xem đáp án
Xem đáp án
Ta có và là hai vecto có giá song song hoặc nằm trên mặt phẳng (P) nên mặt phẳng (P) có một vecto pháp tuyến là .
Vậy mặt phẳng (P) đi qua điểm và có vecto pháp tuyến nên có phương trình là: . Vậy T=2.
Vậy mặt phẳng (P) đi qua điểm và có vecto pháp tuyến nên có phương trình là: . Vậy T=2.
Chọn A
Câu 37:
Cho tam giác ABC có và . Tính thể tích khối tròn xoay nhận được khi quay đường gấp khúc BAC quanh trục BC?
 Xem đáp án
Xem đáp án
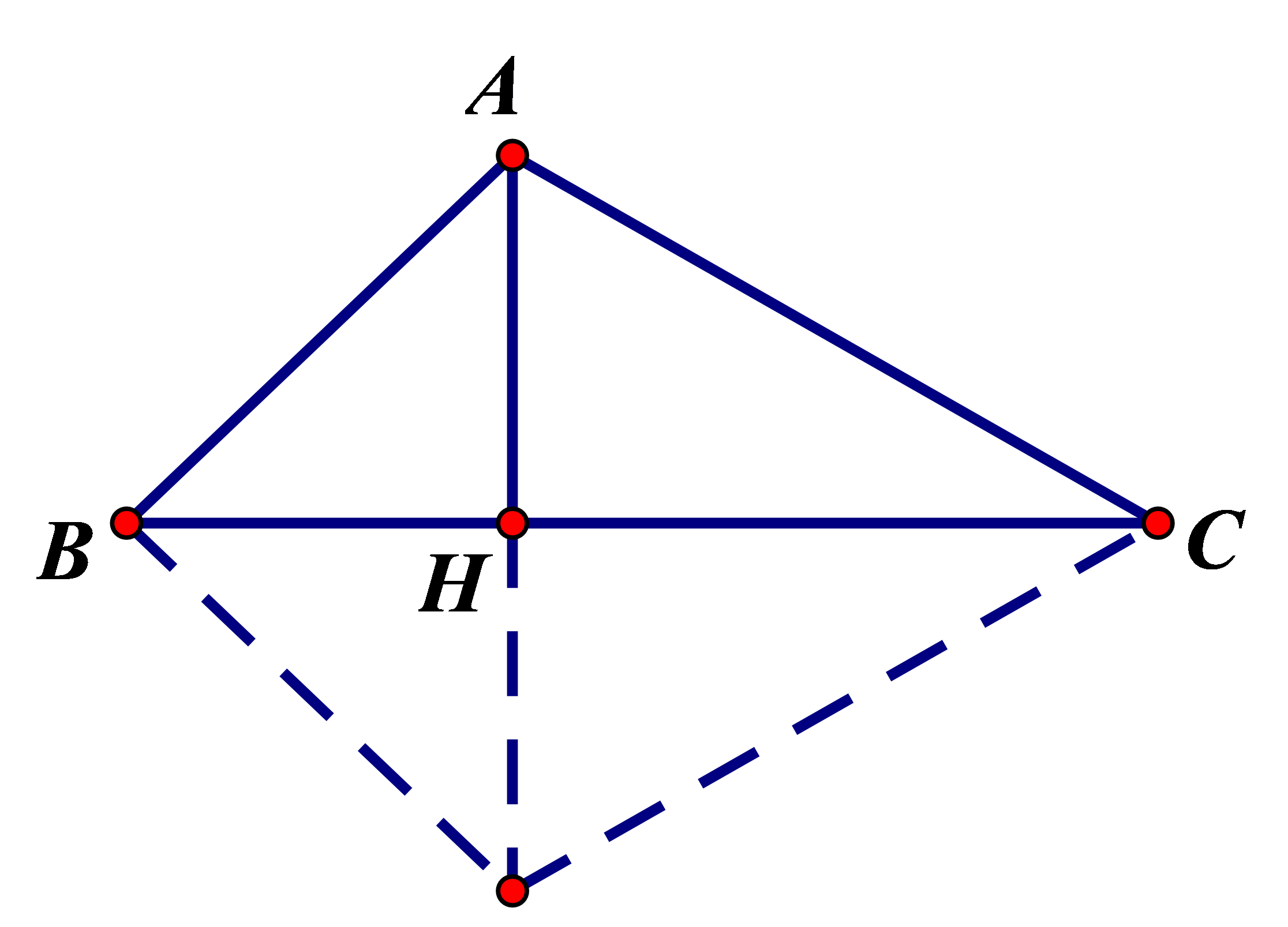
Gọi H là hình chiếu vuông góc của A lên BC.
Xét tam giác ACH vuông tại H, có AC = 2a, nên
và .
Tam giác ABH vuông tại H, có AH = a, nên .
Quay đường gấp khúc BAC quanh trục BC thu được khối tròn xoay có hình dạng là hai khối nón đỉnh B và đỉnh C, chung đáy là đường tròn (H; HA).
Xét khối nón có đỉnh là B, đáy là đường tròn có Xét khối nón có đỉnh là C, đáy là đường tròn (H; HA) có Vậy thể tích khối tròn xoay nhận được bằng: .
Xét tam giác ACH vuông tại H, có AC = 2a, nên
và .
Tam giác ABH vuông tại H, có AH = a, nên .
Quay đường gấp khúc BAC quanh trục BC thu được khối tròn xoay có hình dạng là hai khối nón đỉnh B và đỉnh C, chung đáy là đường tròn (H; HA).
Xét khối nón có đỉnh là B, đáy là đường tròn có Xét khối nón có đỉnh là C, đáy là đường tròn (H; HA) có Vậy thể tích khối tròn xoay nhận được bằng: .
Câu 38:
Cho hàm số f(x) xác định trên và thỏa mãn: . Biết rằng và . Tính .
 Xem đáp án
Xem đáp án
Ta có:
Với : .
Mà
.
Do đó với .
Với : .
Mà
.
Do đó với .
Vậy .
Với : .
Mà
.
Do đó với .
Với : .
Mà
.
Do đó với .
Vậy .
