Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023 (Đề 3)
-
8023 lượt thi
-
39 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số có bảng biến thiên như sau:
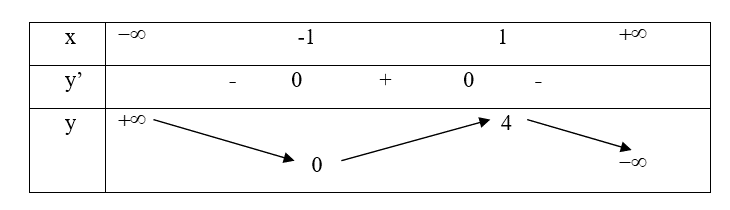
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn A
Dựa vào bảng biến thiên ta thấy nên hàm số đã cho đồng biến trên khoảng Do đó chọn đáp án A.
Dựa vào bảng biến thiên ta thấy nên hàm số đã cho đồng biến trên khoảng Do đó chọn đáp án A.
Câu 2:
Cho hàm số có đồ thị là đường cong trong hình sau. Hàm số đã cho đồng biến trên khoảng nào dưới đây?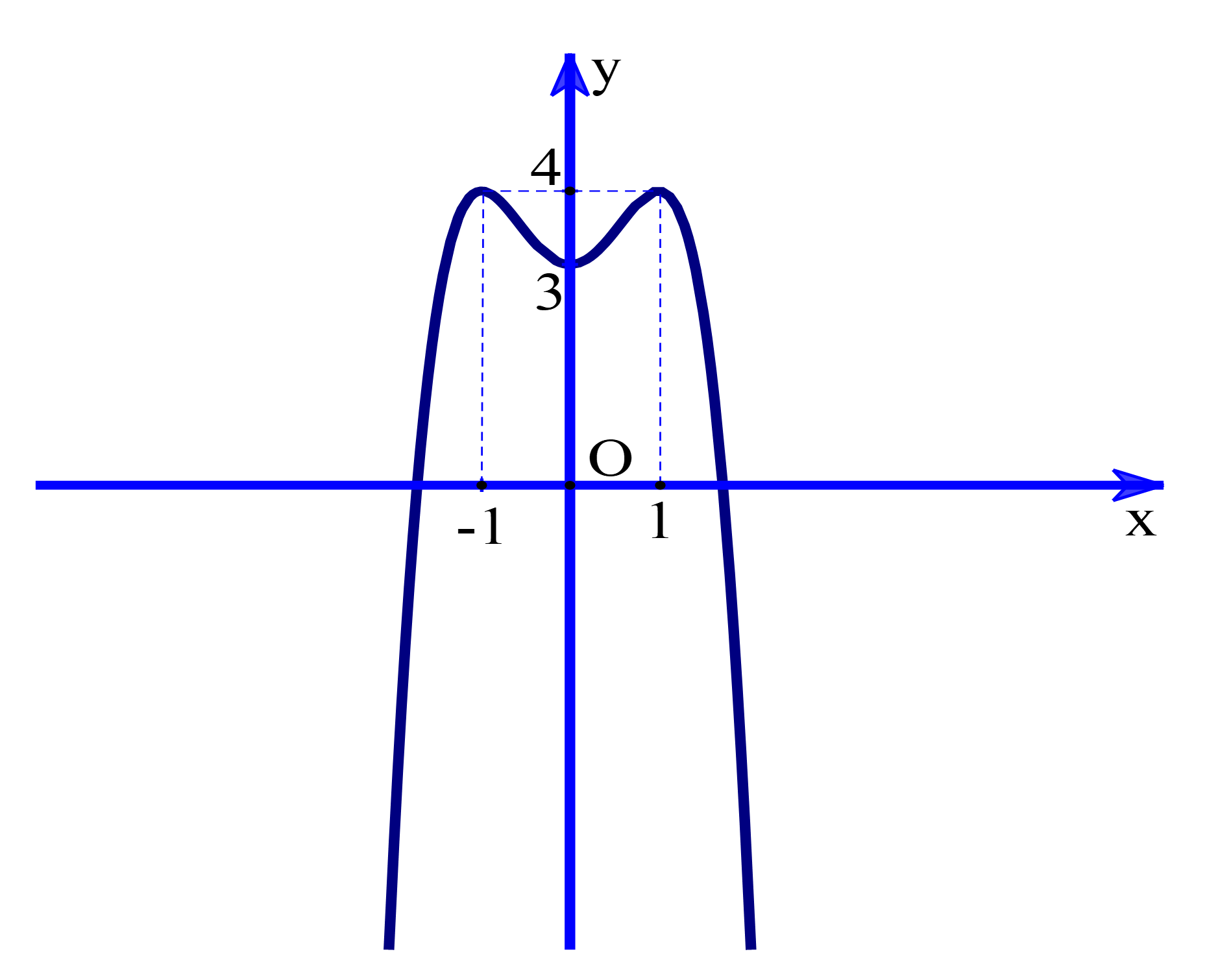
 Xem đáp án
Xem đáp án
Chọn B
Dựa vào đồ thị hàm số ta có hàm số đồng biến trên khoảng Do đó chọn đáp án B.
Dựa vào đồ thị hàm số ta có hàm số đồng biến trên khoảng Do đó chọn đáp án B.
Câu 3:
Cho hàm số có đạo hàm Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn C
Vì nên hàm số nghịch biến trên các khoảng không chứa phần tử -2 mà các khoảng đã cho ở đáp án A, B, D đều có chứa phần tử -2 và khoảng đã cho ở đáp án C không chứa phần tử -2 nên loại các đáp án A, B, D và chọn đáp án C.
Vì nên hàm số nghịch biến trên các khoảng không chứa phần tử -2 mà các khoảng đã cho ở đáp án A, B, D đều có chứa phần tử -2 và khoảng đã cho ở đáp án C không chứa phần tử -2 nên loại các đáp án A, B, D và chọn đáp án C.
Câu 4:
Cho hàm số có bảng biến thiên như sau:
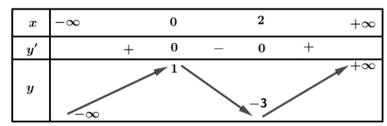
Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Chọn B
Dựa vào bảng biến thiên ta thấy đạo hàm đổi dấu từ âm sang dương khi đi qua nên hàm số đạt cực tiểu tại
Vậy, chọn đáp án B.
Dựa vào bảng biến thiên ta thấy đạo hàm đổi dấu từ âm sang dương khi đi qua nên hàm số đạt cực tiểu tại
Vậy, chọn đáp án B.
Câu 5:
Cho hàm số có đồ thị như hình vẽ bên.
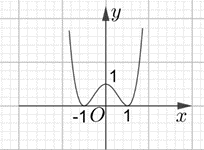
Số điểm cực trị của đồ thị hàm số là
Số điểm cực trị của đồ thị hàm số là
 Xem đáp án
Xem đáp án
Chọn A
Nhìn vào đồ thị của hàm số ta thấy đồ thị hàm số có ba điểm cực trị.
Nhìn vào đồ thị của hàm số ta thấy đồ thị hàm số có ba điểm cực trị.
Câu 6:
Cho hàm số có bảng xét dấu của như sau:

Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Chọn C
Dựa vào bảng xét dấu của ta thấy đạo hàm đổi dấu từ dương sang âm một lần nên hàm
số có một điểm cực đại.
Vậy, chọn đáp án C.
Dựa vào bảng xét dấu của ta thấy đạo hàm đổi dấu từ dương sang âm một lần nên hàm
số có một điểm cực đại.
Vậy, chọn đáp án C.
Câu 7:
Cho hàm số liên tục trên và có bảng xét dấu như sau
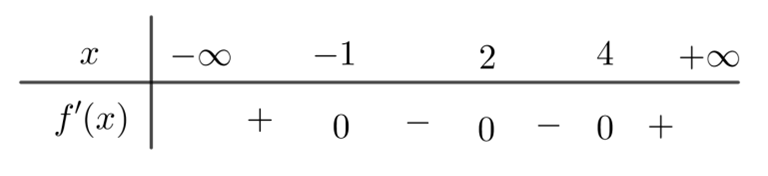
Hàm số có bao nhiêu điểm cực trị?
Hàm số có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Chọn C
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại và đạt cực tiểu tại , nên hàm số có điểm cực trị.
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại và đạt cực tiểu tại , nên hàm số có điểm cực trị.
Câu 8:
Hàm số liên tục và có bảng biến thiên trong đoạn cho trong hình bên. Gọi M là giá trị lớn nhất của hàm số trên đoạn . Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn D
Dựa vào bảng biến thiên ta thấy hàm số có giá trị lớn nhất trên đoạn là 5 nên
Dựa vào bảng biến thiên ta thấy hàm số có giá trị lớn nhất trên đoạn là 5 nên
Câu 9:
Cho hàm số có đồ thị như hình vẽ.
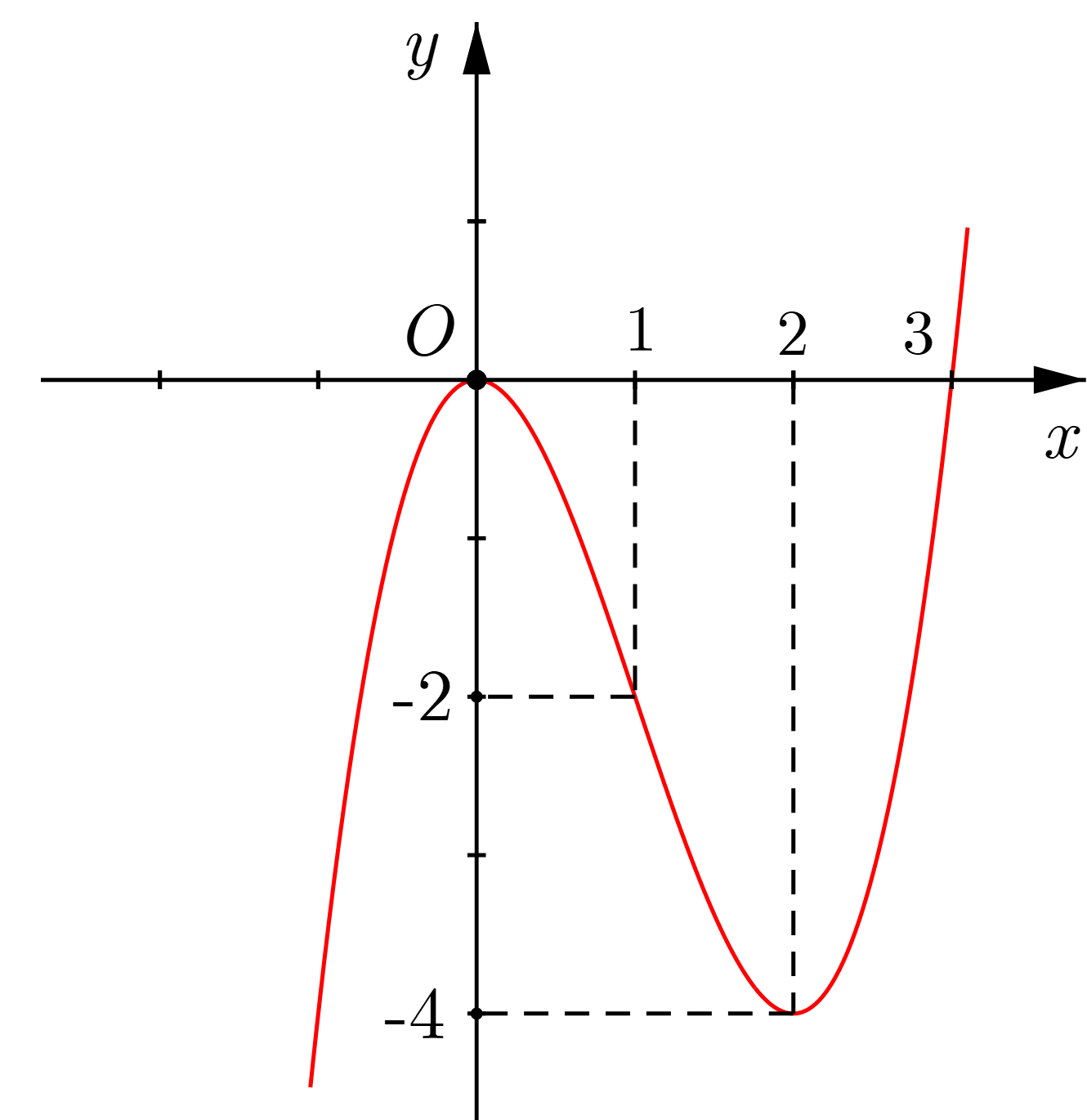
Giá trị nhỏ nhất của hàm số trên đoạn bằng
Giá trị nhỏ nhất của hàm số trên đoạn bằng
 Xem đáp án
Xem đáp án
Chọn D
Dựa vào đồ thị ta thấy hàm số có giá trị nhỏ nhất trên đoạn là -4.
Dựa vào đồ thị ta thấy hàm số có giá trị nhỏ nhất trên đoạn là -4.
Câu 10:
Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn B
Từ hình vẽ suy ra đây là đồ thị hàm số trùng phương.
Hàm số có hai điểm cực tiểu, một điểm cực đại nên hệ số a>0
Từ hình vẽ suy ra đây là đồ thị hàm số trùng phương.
Hàm số có hai điểm cực tiểu, một điểm cực đại nên hệ số a>0
Câu 11:
Đường cong ở hình bên dưới là đồ thị của hàm số nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn A
Từ đồ thị ta thấy đồ thị hàm số giao với trục tung tại điểm .
Trong các phương án đã cho thì hàm số thỏa mãn.
Từ đồ thị ta thấy đồ thị hàm số giao với trục tung tại điểm .
Trong các phương án đã cho thì hàm số thỏa mãn.
Câu 12:
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
Ta có:
Suy ra, đường thẳng là đường tiệm cận ngang của đồ thị hàm số.
Suy ra, đường thẳng là đường tiệm cận đứng của đồ thị hàm số.
Câu 13:
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số ?
 Xem đáp án
Xem đáp án
Chọn A
Ta có: và nên là tiệm cận đứng.
Ta có: và nên là tiệm cận đứng.
Câu 14:
Cho hàm số có và . Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Chọn D
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
Câu 15:
Cho các hình sau:
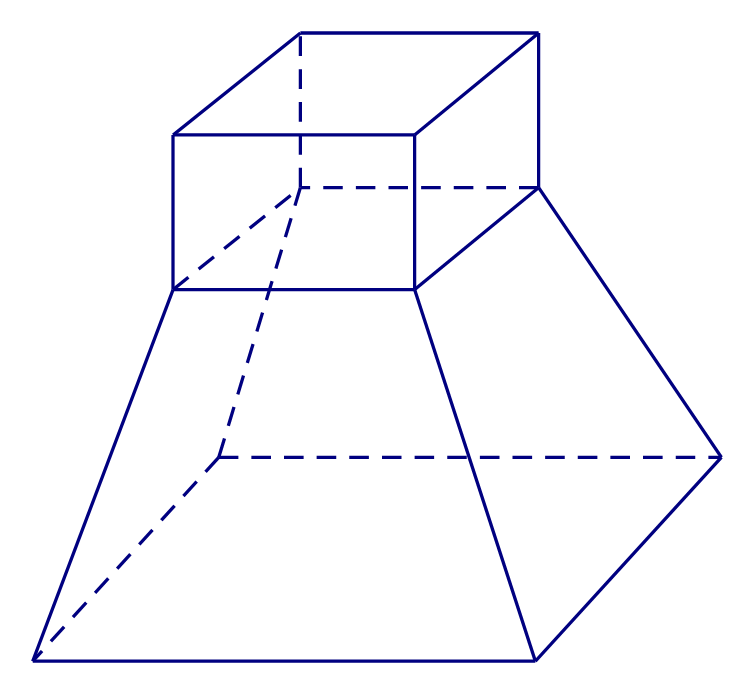
Hình 1
Hình 1
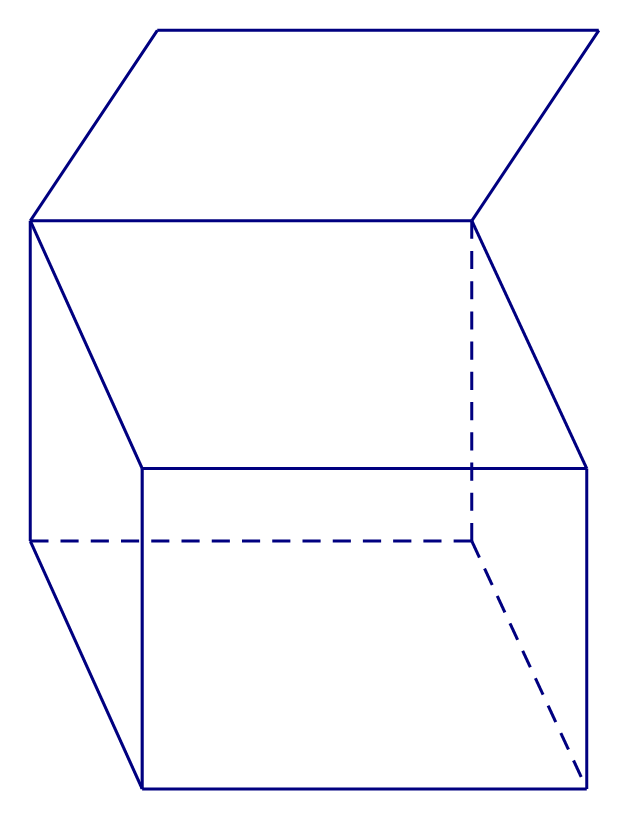
Hình 2

Hình 3
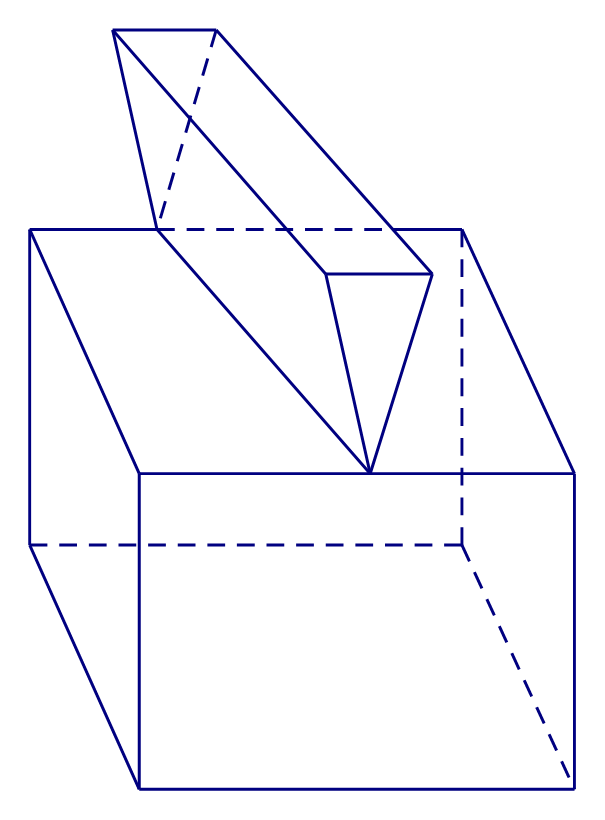
Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
 Xem đáp án
Xem đáp án
Chọn A
Hình đa diện là hình tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
1. Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung hoặc chỉ có một đỉnh chung hoặc chỉ có một cạnh chung.
2. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Các hình 2, 3, 4 đều không thỏa mãn tính chất số 2.
Hình đa diện là hình tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
1. Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung hoặc chỉ có một đỉnh chung hoặc chỉ có một cạnh chung.
2. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Các hình 2, 3, 4 đều không thỏa mãn tính chất số 2.
Câu 17:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Tính thể tích của khối chóp.
 Xem đáp án
Xem đáp án
Chọn D.
Câu 18:
Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng
 Xem đáp án
Xem đáp án
Chọn B.
Câu 20:
Tính thể tích chóp biết chiều cao là , diện tích đáy .
 Xem đáp án
Xem đáp án
Chọn B
Thể tích khối chóp là:
Thể tích khối chóp là:
Câu 21:
Cho hàm số có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn C
Giá trị hàm số tăng khi x tăng từ 0 đến 2 nên hàm số đồng biến trên khoảng (0;2)
Giá trị hàm số tăng khi x tăng từ 0 đến 2 nên hàm số đồng biến trên khoảng (0;2)
Câu 22:
Cho hàm số Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn C
Ta có
Bảng biến thiên
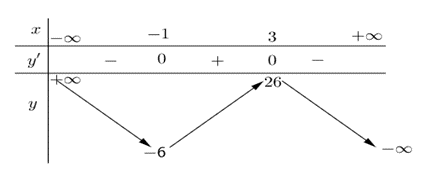
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng , ngịch biến trên các khoảng và
Ta có
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng , ngịch biến trên các khoảng và
Câu 23:
Cho hàm số xác định và có đạo hàm cấp một và cấp hai trên khoảng và Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Chọn A
Phản ví dụ câu A: hàm số có
Nhưng hàm số không đạt cực trị tại
Phản ví dụ câu A: hàm số có
Nhưng hàm số không đạt cực trị tại
Câu 24:
Cho hàm số xác định, liên tục trên và có bảng biến thiên
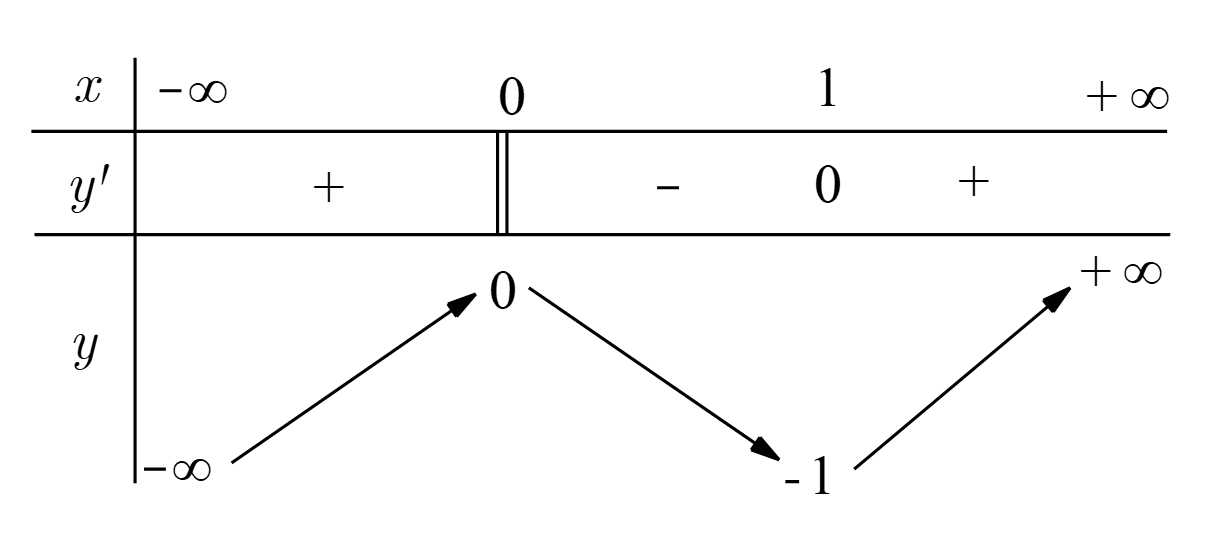
Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn D
Câu 26:
Giá trị lớn nhất của hàm số trên đoạn bằng:
 Xem đáp án
Xem đáp án
Chọn B
Hàm số liên tục và xác định trên .
Ta có: .
.
; ; ; .
Vậy .
Hàm số liên tục và xác định trên .
Ta có: .
.
; ; ; .
Vậy .
Câu 27:
Đường cong sau đây là đồ thị của hàm số nào?
 Xem đáp án
Xem đáp án
Chọn C
Từ đồ thị ta có: Hàm số bậc ba nên loại A, D.
Hệ số a>0 nên loại B.
Từ đồ thị ta có: Hàm số bậc ba nên loại A, D.
Hệ số a>0 nên loại B.
Câu 28:
Cho hàm số có đồ thị như hình vẽ bên dưới. Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Chọn D
Dựa vào đồ thị ta thấy, phương trình có hai nghiệm phân biệt khi .
Dựa vào đồ thị ta thấy, phương trình có hai nghiệm phân biệt khi .
Câu 29:
Cho hàm số bậc ba có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình là:
 Xem đáp án
Xem đáp án
Chọn A
Số nghiệm thực của phương trình chính là số giao điểm của đồ thị hàm số và đường thẳng .
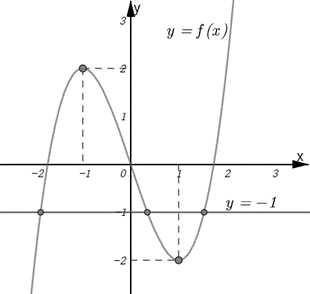
Từ hình vẽ suy ra 3 nghiệm.
Số nghiệm thực của phương trình chính là số giao điểm của đồ thị hàm số và đường thẳng .
Từ hình vẽ suy ra 3 nghiệm.
Câu 30:
Tiệm cận ngang của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Chọn D
Ta có . Suy ra đồ thị hàm số có tiệmcận ngang là .
Ta có . Suy ra đồ thị hàm số có tiệmcận ngang là .
Câu 31:
Đồ thị hàm số có tất cả bao nhiêu tiệm cận?
 Xem đáp án
Xem đáp án
Chọn C
Nên đồ thị hàm số đã cho nhận đường thẳng làm tiệm cận đứng.
Nên đồ thị hàm số đã cho nhận đường thẳng làm tiệm cận ngang.
Vậy đồ thị hàm số có 3 tiệm cận.
Nên đồ thị hàm số đã cho nhận đường thẳng làm tiệm cận đứng.
Nên đồ thị hàm số đã cho nhận đường thẳng làm tiệm cận ngang.
Vậy đồ thị hàm số có 3 tiệm cận.
Câu 32:
Khẳng định nào sau đây là đúng khi nói về số cạnh của hình đa diện đều.
 Xem đáp án
Xem đáp án
Chọn B
Xét tứ diện đều có 6 cạnh, dễ thấy số cạnh của khối đa diện luôn lớn hơn hoặc bằng 6.
Xét tứ diện đều có 6 cạnh, dễ thấy số cạnh của khối đa diện luôn lớn hơn hoặc bằng 6.
Câu 33:
Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Chọn D
Khối tứ diện đều có các mặt của nó là những tam giác đều.
Hình lập phương là khối đa diện đều mà các mặt của nó là những hình vuông.
Khối mười hai mặt đều là khối đa diện đều mà các mặt của nó là những ngũ giác đều.
Tồn tại hình đa diện đều mà các mặt của nó là những lục giác đều là sai.
Khối tứ diện đều có các mặt của nó là những tam giác đều.
Hình lập phương là khối đa diện đều mà các mặt của nó là những hình vuông.
Khối mười hai mặt đều là khối đa diện đều mà các mặt của nó là những ngũ giác đều.
Tồn tại hình đa diện đều mà các mặt của nó là những lục giác đều là sai.
Câu 35:
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A.
Ta có:
Chọn A.
Ta có:
Câu 36:
Cho hàm số . Hàm số có đồ thị như hình bên. Hàm số nghịch biến trên khoảng nào ?
 Xem đáp án
Xem đáp án
Ta có :
Đặt
Đặt
Vẽ đường thẳng và đồ thị hàm số trên cùng một hệ trục
Hàm số nghịch biến
Như vậy .
Vậy hàm số nghịch biến trên các khoảng và .
Câu 37:
Cho lăng trụ ABC.A'B'C' có chiều cao bằng 4 và đáy là tam giác đều cạnh bằng 4. Gọi M, N và P lần lượt là tâm của các mặt bên và . Thể tích của khối đa diện lồi có các đỉnh là các điểm bằng?
 Xem đáp án
Xem đáp án
Thể tích khối lăng trụ là .
Gọi thể tích của khối đa diện lồi có các đỉnh là các điểm là .
Ta có: .
Dễ thấy và nên .
và nên .
và nên .
Vậy .
Gọi thể tích của khối đa diện lồi có các đỉnh là các điểm là .
Ta có: .
Dễ thấy và nên .
và nên .
và nên .
Vậy .
Câu 38:
Cho hàm số có đồ thị như hình vẽ:
Tìm điểm cực tiểu của hàm số .
 Xem đáp án
Xem đáp án
Ta có: .
.
Đồ thị hàm số nhận được từ việc tịnh tiến đồ thị hàm số sang trái 1 đơn vị.
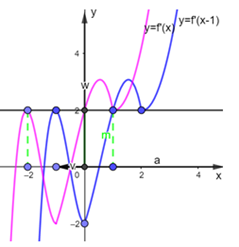
Nên .
Vì là các nghiệm bội chẵn nên ta có bảng biến thiên như sau:
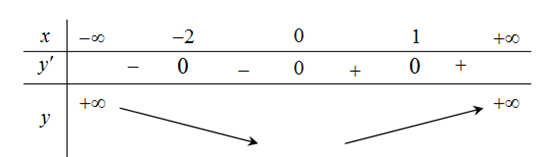
Từ bảng biến thiên suy ra hàm số đã cho điểm cực tiểu là .
.
Đồ thị hàm số nhận được từ việc tịnh tiến đồ thị hàm số sang trái 1 đơn vị.
Nên .
Vì là các nghiệm bội chẵn nên ta có bảng biến thiên như sau:
Từ bảng biến thiên suy ra hàm số đã cho điểm cực tiểu là .
Câu 39:
Cho hàm số . Tìm m để .
 Xem đáp án
Xem đáp án
Xét hàm số trên đoạn .
Ta có: .
.
Suy ra: .
Trường hợp 1: .
Trường hợp 2: .
Vậy thỏa bài toán.
