Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 5
-
4564 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
= = – 5 + 7 = 2.
Vậy ta chọn phương án D.
Câu 2:
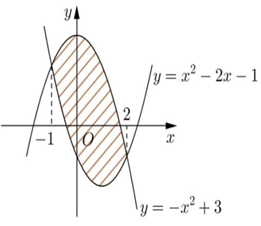
Diện tích phần hình phẳng được gạch chéo trong hình vẽ bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình hoành độ giao điểm của 2 hàm số là:
−x2 + 3 = x2 – 2x – 1
Û −x2 + 3 – x2 + 2x + 1 = 0
Û −2x2 + 2x + 4 = 0
Û
Diện tích hình phẳng là: S =
Vậy ta chọn phương án B.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
= −
= −
= 3.2 – (4 – 0) = 2
Vậy = 2
Câu 4:
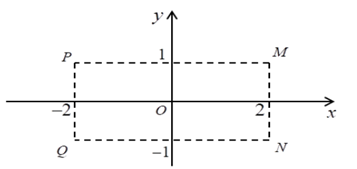
Điểm nào trong hình vẽ là điểm biểu diễn của số phức z = 2 – i ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
z = 2 – i có tọa độ điểm biểu diễn là (2; −1)
Vậy z = 2 – i có điểm biểu diễn là N(2; −1)
Câu 5:
Trong không gian Oxyz, cho mặt phẳng (P) : x − 2y + 1 = 0. Một vectơ pháp tuyến của (P) có tọa độ là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vectơ pháp tuyến của mặt phằng (P) là (1; −2; 0).
Vậy ta chọn phương án B.
Câu 6:
Trong không gian Oxyz, đường thẳng d đi qua điểm M(−1; 2; 1) vuông góc với mặt phẳng (P): x – 2y + 1 = 0 có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vectơ pháp tuyến của mặt phẳng (P): x – 2y + 1 = 0 là (1; −2; 0).
Do d vuông góc với (P) nên vectơ pháp tuyến của (P) là vectơ chỉ phương của d.
d đi qua M(−1; 2; 1) và có vectơ chỉ phương là (1; −2; 0) có phương trình là:
Với t = 1 ta có:
Khi đó đường thẳng d đi qua điểm có tọa độ (0; 0; 1)
Do đó đường thẳng d đi qua điểm (0; 0; 1) và có vectơ chỉ phương là (1; −2; 0) nên có phương trình là:
Vậy ta chọn phương án B.
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Điểm O(0; 0; 0), A(−4; 3; 12).
Þ = (−4; 3; 12).
Þ OA = = 13.
Vậy ta chọn phương án C.
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đặt u = 1 – 3x
Û du = −3dx
Û dx = du
Đổi cận:
|
x |
0 |
|
|
u |
0 |
1 |
Do đó ta được:
=
= = = . 6 = 2
Vậy = 2
Câu 9:
Trong không gian Oxyz, cho đường thằng d : . Một vectơ chỉ phương của d là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vectơ chỉ phương của đường thẳng d là: = (1; −1; 2).
Vậy ta chọn phương án A.
Câu 10:
Cho số phức z tùy ý. Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
|z| = Þ |z|2 = a2 + b2
z2 = (a + bi)2 = a2 – b2 + 2abi
Nên z2 ≠ |z|2
Vậy ta chọn phương án A.
Câu 11:
Gọi z1 , z2 là hai nghiệm phức của phương trình z2 – 3z + 5 = 0. Môđun của số phức (2 − 3)(2 − 3) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: z2 – 3z + 5 = 0
Áp dụng hệ thức Viet ta có:
Û
Ta có: (2 − 3)(2 − 3)
= 4 − 6( + ) + 9
= 4.5 – 6.3 + 9
= 11
Vậy (2 − 3)(2 − 3) = 11.
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thay tọa độ các điểm N, Q, M, P vào phương trình của d:
• Với N(0; 0; 1) ta có: .
Do đó N ∉ d.
• Với Q(6; −3; −3) ta có:
Do đó Q ∉ d.
• Với M(4; −2; 2) ta có:
Do đó M ∈ d.
• Với P(−2; −1; −1) ta có:
Do đó P ∉ d.
Vậy ta chọn phương án C.
Câu 13:
Cho hàm số y = f(x) liên tục và không âm trên đoạn [a; b]. Gọi hình phẳng (H) giới hạn bởi các đường y = f(x), y = 0, x = a và x = b. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh Ox bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh Ox là:
V =
Câu 14:
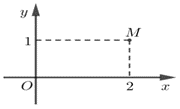
Biết rằng điểm M trong hình vẽ là điểm biểu diễn của số phức z. Môđun của z bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát hình vẽ ta thấy tọa độ của M là M(2; 1)
Do đó điểm M biểu diễn số phức z = 2 + i
Vậy |z| = =
Câu 15:
Cho hai số phức z = 3 + 4i và w = 1 − 3i. Số phức z – 2w bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
2w = 2(1 – 3i) = 2 – 6i
Nên z – 2w = 3 + 4i – 2 + 6i = 1 + 10i.
Câu 16:
Họ tất cả các nguyên hàm của hàm số f(x) = e−x là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: = −e−x + C.
Vậy ta chọn phương án A.
Câu 17:
Cho số phức z thỏa mãn iz = 4 – 3i. Số phức liên hợp của z là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: iz = 4 – 3i
Þ z = =
= = = −3 – 4i
Số phức liên hợp của z là = −3 + 4i.
Câu 18:
Cho các số phức z1 = 3 + 2i; z2 = 3 – 2i. Phương trình bậc hai có nghiệm z1, z2 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Với z1 = 3 + 2i; z2 = 3 – 2i ta có:
Mà i2 = −1
Nên
Do đó z1, z2 là hai nghiệm của phương trình : z2 – Sz + P = 0
Û z2 – 6z + 13 = 0.
Vậy ta chọn phương án C.
Câu 19:
Trong không gian Oxyz, cho hai vectơ = (1; ; 0) và = (−1; 0; 0). Góc giữa và bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Với = (1; ; 0) và = (−1; 0; 0) ta có:
cos(, ) = = =
Nên góc giữa hai vectơ và là: (; ) = 120°.
Vậy ta chọn phương án B.
Câu 20:
Cho hàm số f(x) = sin3x . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: = cos3x + C.
Vậy ta chọn phương án D.
Câu 21:
Họ tất cả các nguyên hàm của hàm số f(x) = trên khoảng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: = ln|2 – 3x| + C
Vì x ∈ nên |2 – 3x| = 3x – 2
Do đó = ln(3x – 2) + C.
Vậy ta chọn phương án D.
Câu 22:
Họ tất cả các nguyên hàm của số f(x) = x3 + là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
= +
= − + C.
Vậy ta chọn phương án C.
Câu 23:
Biết = 4. Giá trị của bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:
= −
= 2.4 − = 8 – (3 – 1) = 6.
Vậy ta chọn phương án D.
Câu 24:
Cho hàm số f(x) liên tục trên đoạn [1; 3]. Biết F(x) là nguyên hàm của f(x) trên đoạn [1; 3] thỏa mãn F(1) = −2 và F(3) = 5. Khi đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: = = F(3) – F(1) = 5 – (−2) = 7.
Vậy ta chọn phương án B.
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phương trình hoành độ giao điểm của đồ thị hàm số f(x) với trục hoành là:
x4 – 5x + 4 = 0 Û
Khi đó ta có:
S = = 2
= 2 + 2
= 2 + 2
Do đó phương án D là sai.
Vậy ta chọn phương án D.
Câu 26:
Môđun của số phức z = 4 – 3i bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Với z = 4 – 3i ta có: |z| = = 5
Vậy môđun của z = 4 – 3i bằng 5.
Câu 27:
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y + 2z – 1 = 0. Khoảng cách từ điểm A(1; –2; 1) đến mặt phẳng (P) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Với A(1; –2; 1) và (P): x – 2y + 2z – 1 = 0 ta có:
d(A; (P)) = = 2
Vậy khoảng cách từ A đến (P) bằng 2.
Câu 28:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: z =
= =
=
=
Þ |z| = =
Vậy ta chọn phương án B.
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
z = 3 – 5i có phần ảo là −5.
Vậy ta chọn phương án A.
Câu 30:
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và với mọi a, b, k ∈ ℝ. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đáp án C sai do:
= k. (với hệ số k khác 0).
Vậy ta chọn phương án C.
Câu 31:
Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 – 2x + 4y + 2z – 3 = 0. Tâm của (S) có tọa độ là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Mặt cầu (S): x2 + y2 + z2 – 2x + 4y + 2z – 3 = 0 có các hệ số của x, y, z lần lượt là –2; 4; 2.
Do đó mặt cầu (S) có tâm là (1; −2; −1).
Câu 32:
Trong không gian Oxyz, cho điểm M(−2; 3; 1) và N(1; −2; 0). Đường thẳng MN có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Với M(−2; 3; 1) và N(1; −2; 0) ta có:
= (3; −5; −1)
Đường thẳng MN đi qua N(1; −2; 0) và có vectơ = (3; −5; −1) là:
Vậy ta chọn phương án A.
Câu 33:
Trong không gian Oxyz, cho điểm M(1; −2; 1) và mặt phẳng (P): 2x + y – 2z + 1 = 0. Mặt phẳng đi qua M và song song với (P) có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Mặt phẳng (P): 2x + y – 2z + 1 = 0 có vectơ pháp tuyến là (2; 1; –2)
Gọi mặt phẳng cần tìm là (Q)
Do (Q) // (P) nên vectơ pháp tuyến của (P) cũng là vectơ pháp tuyến của (Q)
Phương trình mặt phẳng (Q) đi qua M(1; −2; 1) và có vectơ pháp tuyến là (2; 1; −2) là:
2(x – 1) + 1(y + 2) – 2(z – 1) = 0
Û 2x – 2 + y + 2 – 2z + 2 = 0
Û 2x + y – 2z + 2 = 0
Vậy (Q): 2x + y – 2z + 2 = 0.
Câu 34:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi số phức z = a + bi, (a, b ∈ ℝ)
Þ = a – bi .
Khi đó ta có:
z + 2 = 6 + 2i
Û a + bi + 2(a – bi) = 6 + 2i
Û 3a – bi = 6 + 2i
Û Û (thỏa mãn)
Suy ra z = 2 − 2i
Vậy M(2 ; −2) là điểm biểu diễn số phức z.
Câu 35:
Biết phương trình z2 − 2z + 3 = 0 có hai nghiệm phức z1, z2. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình z2 – 2z + 3 = 0 có hai nghiệm là:
z1 = 1 + i và z2 = 1 − i
Ta có:
• z1 + z2 = 1 + i + 1 – i
Þ z1 + z2 = 2 là một số thực.
Do đó A là đúng.
• z1 – z2 = 1 + i – (1 – i)
Þ z1 – z2 = 2i là một số ảo
Nên z1 – z2 là số thực là sai.
Do đó B là sai.
Vậy ta chọn phương án B.
Câu 36:
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y + 2z – 1 = 0. Mặt cầu có tâm thuộc tia Ox, bán kính bằng 2 và tiếp xúc với (P) có phương trình
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi (S) là phương trình mặt cầu cần tìm có tâm thuộc tia Ox nên I(a; 0; 0) (a ≥ 0).
(S) tiếp xúc với mặt phẳng (P): x – 2y + 2z – 1 = 0 nên khoảng cách d(I; (P)) = R
Û = 2
Û = 2
Û |a – 1| = 6
Û
Do a ≥ 0 nên ta lấy a = 7
Vậy (S) : (x – 7)2 + y2 + z2 = 4.
Câu 37:
Trong không gian Oxyz, cho mặt cầu (S): (x – 1)2 + (y − 2)2 + (z + 1)2 = 6, tiếp xúc với hai mặt phẳng (P): x + y + 2z + 5 = 0 và (Q): 2x – y + z – 5 = 0 lần lượt tại hai điểm A và B. Độ dài đoạn thẳng AB bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Mặt cầu (S): (x – 1)2 + (y − 2)2 + (z + 1)2 = 6 có tâm I(1; 2; −1).
Mặt phẳng (P): x + y + 2z + 5 = 0 có vectơ pháp tuyến là = (1; 1; 2).
Mặt phẳng (Q): 2x – y + z – 5 = 0 có vectơ pháp tuyến là = (2; –1; 1).
• Gọi A(x; y; z) là tiếp điểm (S) và (P).
Þ
Vì A là là tiếp điểm (S) và (P) nên ta có:
Mà A ∈ (P) nên ta có: x + y + 2z + 5 = 0
Þ k + 1 + k + 2 + 2(2k – 1) + 5 = 0
Þ 6k = –6
Þ k = –1
Þ A(0; 1; −3)
• Gọi B(x'; y'; z') là tiếp điểm của mặt phẳng (Q): 2x – y + z − 5 = 0 và mặt cầu (S)
Khi đó : Û
Tương tự như trên ta tìm được B(3; 1; 0).
Với A(0; 1; −3) và B(3; 1; 0) ta có:
Độ dài AB = =
Vậy ta chọn phương án D.
Câu 38:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
F(x) = x2 là nguyên hàm của f(x)sin2x
Nên F'(x) = f(x)sin2x
Û 2x = f(x)sin2x Û f(x) =
G(x) là nguyên hàm của f(x)cos2x
Do đó G(x) = =
= =
= − x2
= −2xcotx + − x2
= −2xcotx – x2 + 2
= −2xcotx – x2 + 2ln|sinx| + C
Theo giả thiết:
• G = 0
Û + C = 0 Û C =
Nên G(x) = −2xcotx – x2 + 2ln|sinx| +
•
=
=
=
Mà G = aπ + bπ2 + cln2
Nên ta có: a = ; b = ; c = −1
Vậy a + b + c = + − 1 = .
Câu 39:
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0; 1] và f(1) = . Tích phân bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta tính như sau:
Đặt:
Vậy ta chọn phương án A.
Câu 40:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đặt z = a + bi , w = c + di (a, b, c, d ∈ ℝ ).
Þ iw – 2 + 5i = i(c + di) – 2 + 5i
= ci + di2 – 2 + 5i
= (c + 5)i – d – 2
Khi đó ta có:
• |z| = Þ a2 + b2 = 4
Þ a, b ∈ [–2; 2]
• |iw – 2 + 5i| =
Þ (c + 5)2 + (d + 2)2 = 1
Þ c ∈ [–6; –4] và d ∈ [–3; –1].
Ta có:
T = |z2 – wz – 4|
= |z2 – wz − |z|2|
= |z2 – wz – z . |
= |z| . |z − − w|
= 2|z − − w|
Þ T = 2|2bi – (c + di)|
= 2|– c + (2b – d)i|
= 2 ≥ 2 = 2|c| ≥ 2.4 = 8
(do c ∈ [−6; −4] nên |c| ≥ 4)
Dấu “=” xảy ra khi và chỉ khi : Þ
Vậy |z2 – wz – 4| có giá trị nhỏ nhất bằng 8.
Câu 41:
Trong không gian Oxyz, cho hai điểm A(10; 6; −2), B(5; 10; −9) và mặt phẳng (α): 2x + 2y + z – 12 = 0. Điểm M thay đổi thuộc mặt phẳng (α) sao cho hai đường thẳng MA và MB luôn tạo với (α) các góc bằng nhau. Biết rằng điểm M luôn thuộc một đường tròn cố định. Hoành độ của tâm đường tròn đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Mặt phẳng (α) có phương trình: 2x + 2y + z – 12 = 0.
Gọi H và K lần lượt là hình chiếu của A và B lên (α).
• Với A(10; 6; −2) ta có:
AH = d(A;(α)) = = 6
• Với B(5; 10; −9) ta có:
BK = d(B;(α)) = = 3
Vì điểm M di động trên mặt phẳng (α) sao cho MA, MB luôn tạo với (α) các góc bằng nhau nên ta có sin = sin
Þ MA = 2MB
Gọi M(x; y; z).
MA = 2MB Û MA2 = 4MB2
Û (x – 10)2 + (y – 6)2 + (z + 2)2 = 4[(x – 5)2 + (y – 10)2 + (z + 9)2]
Û x2 – 20x + 100 + y2 – 12y + 36 + z2 + 4z + 4
= 4x2 – 40x + 100 + 4y2 – 80y + 400 + 4z2 + 72z + 324
Û 3x2 + 3y2 + 3z2 – 20x – 68y + 68z + 684 = 0
Û x2 + y2 + z2 − x − y + z + 228 = 0
Suy ra điểm M thỏa mãn
Mặt cầu (S) có tâm I.
Gọi (ω) là đường tròn cố định luôn đi qua M.
Do đó M ∈ (ω) là giao tuyến của (α) và (S).
Þ Tâm N của (ω) là hình chiếu của tâm I trên mặt phẳng (α).
Mặt phẳng (α): 2x + 2y + z – 12 = 0 có vectơ pháp tuyến là (2; 2; 1).
Phương trình đường thẳng d qua I và vuông góc với (α) là:
Vì N là hình chiếu của I lên (α) nên N ∈ d.
Þ
Mà N ∈ (α) nên ta có:
Þ 20 + 12t + 68 + 12t – 34 + 3t – 36 = 0
Þ 27t = –18
Þ t =
Suy ra điểm N(2; 10; −12)
Vậy hoành độ của tâm đường tròn (ω) bằng 2.
Câu 42:
Cho hàm số f(x) thỏa mãn f(x) + f '(x) = e−x, ∀ x ∈ ℝ và f(0) = 2. Tất cả các nguyên hàm của f(x)e2x là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: f(x) + f '(x) = e−x
Û f(x)ex + f '(x)ex = e−x .ex = 1
Û [f (x)ex]' = 1
Û f(x)ex = x + C'
Vì f(0) = 2 nên ta có:
2.e0 = 0 + C'
Þ C' = 2
Þ f(x)ex = x + 2
Þ f(x)e2x = (x + 2).ex
Khi đó ta có:=
=
= (x + 2)ex −
= (x + 2)ex −
= (x + 2)ex – ex + C
= (x + 1)ex + C.
Vậy ta chọn phương án B.
Câu 43:
Có bao nhiêu giá trị nguyên của tham số m để phương trình z2 – 2mz + 6m – 5 = 0 có hai nghiệm phức phân biệt z1, z2 thỏa mãn |z1| = |z2|?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Phương trình z2 – 2mz + 6m – 5 = 0 có hai nghiệm phức phân biệt z1, z2
Û D' = (–m)2 – 1.(6m – 5) < 0
Û m2 – 6m + 5 < 0
Û 1 < m < 5.
Khi đó hai nghiệm phức của phương trình là hai số phức liên hợp của nhau nên ta luôn có |z1| = |z2|
Mà m ∈ ℤ
Þ m = {2; 3; 4}
Vậy có 3 giá trị m thỏa mãn.
Câu 44:
Biết rằng = aln2 + bln3 + cln5, với a, b, c ∈ ℚ. Giá trị a + b + c bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
=
=
Đặt u =
Û u2 = 3x + 1
Û 2udu = 3dx
Û dx = u.du
Đổi cận
|
x |
0 |
1 |
|
u |
1 |
2 |
Do đó:
=
=
= .(3ln5 – 2ln4 – 3ln4 + 2ln3)
= .(3ln5 – 5ln4 + 2ln3)
= .(3ln5 −10ln2 + 2ln3)
= ln2 + ln3 + 2ln5
Mà = aln2 + bln3 + cln5
Þ a = −; b = ; c = 2
Þ a + b + c = − + + 2 =
Vậy a + b + c =
Câu 45:
 Xem đáp án
Xem đáp án
Đáp án đúng là : D
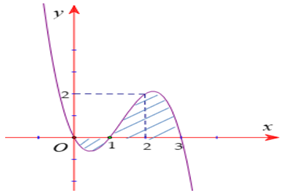
Quan sát hình vẽ ta thấy đồ thị đi qua O(0; 0), A(1; 0), B(2; 2) và C(3; 0) nên ta có:
Û
Ta được hàm số là y = −x3 + 4x2 – 3x.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = −x3 + 4x2 – 3x và trục hoành là:
S =
=
Vậy diện tích bằng
Câu 46:
Có bao nhiêu số phức z thỏa mãn |z – 1|2 + |z − |i + (z + )i2023 = 1?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi z = a + bi (a, b ∈ ℝ)
Þ = a – bi
Ta có:
• z – 1 = a – 1 + bi
Þ |z – 1|2 = (a – 1)2 + b2.
• z − = 2bi
Þ
Þ
• z + = 2a
• i2023 = . i = −i
Þ (z + )i2023 = –2ai
Do đó: |z – 1|2 + |z − |i + (z + )2023 = 1
Û (a – 1)2 + b2 + 2|b|i – 2ai = 1
Û (a – 1)2 + b2 + (2|b| – 2a)i = 1
Û Û
Û
• Với a = 0 ta có b = 0 khi đó ta có z = 0.
• Với a = 1 ta có |b| = 1 Þ b = 1 hoặc b = –1
Khi đó ta có z = 1 + i; z = 1 – i.
Vậy có 3 số phức z thỏa mãn yêu cầu bài toán.
Câu 47:
Trong không gian Oxyz, cho ba đường thẳng d: ∆1: và ∆2: . Đường thẳng ∆ vuông góc với d đồng thời cắt ∆1, ∆2 lần lượt tại H, K sao cho HK nhỏ nhất. Biết rằng ∆ có một vectơ chỉ phương (h; k; 1). Giá trị h – k bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Giả sử H(3 + 2t; t; 1 + t) ∈ ∆1 và K(1 + t'; 2 + 2t'; t') ∈ ∆2
Ta có: = (t' – 2t – 2; 2t' – t + 2; t' – t – 1)
Đường thẳng d: có vectơ chỉ phương là = (1; 1; −2)
Vì d ^ ∆ nên ^ Þ . = 0
Û t' – 2t – 2 + 2t' – t + 2 – 2(t' – t – 1) = 0
Û t' – t + 2 = 0 Û t' = t – 2
Nên = (−t – 4; t – 2; −3)
Þ HK2 = (t + 4)2 + (t – 2)2 + 9
Û HK2 = 2t2 + 4t + 29 = 2(t + 1)2 + 27 ≥ 27 ∀ t
Þ HKmin = Û t = −1 .
Khi đó = (−3; −3; −3) song song với vectơ (1; 1; 1)
Suy ra đường thẳng ∆ nhận (1; 1; 1) là một vectơ chỉ phương nên h = k = 1
Vậy h – k = 1 – 1 = 0
Vậy h – k = 0.
Câu 48:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: f(x) = x3 + ax2 + bx + c
Þ f '(x) = 3x2 + 2ax + b
Þ f "(x) = 6x + 2a
Þ g(x) = f(x) + f '(x) + f "(x)
= x3 + ax2 + bx + c + 3x2 + 2ax + b + 6x + 2a
= x3 + (a + 3)x2 + (2a + b + 6)x + 2a + b + c
Þ g '(x) = 3x2 + 2(a + 3)x + 2a + b + 6
Hàm số g '(x) = 0 có 2 nghiệm x1 và x2 (x1 < x2) cũng là 2 điểm cực trị của y = g(x)
Nên g(x1) = 2; g(x2) = –4 (do g(x) là hàm số bậc ba có hệ số của x3 là 1 > 0)
Ta có phương trình hoành độ giao điểm là:
Ta có g(x) = f(x) + f '(x) + f "(x)
Þ f(x) – g(x) = –[f '(x) + f "(x)]
= –(3x2 + 2ax + b + 6x + 2a)
= –[3x2 + (2a + 6)x + b + 2a]
Do đó ta có:
Û g '(x) = 0
Þ S = =
= |ln|g(x2) + 6| – ln|g(x1) + 6||
= |ln(−4 + 6) – ln(2 + 6)|
= |ln2 – ln8|
= ln8 – ln2
= 3ln2 – ln2
= 2ln2
Vậy diện tích cần tìm là 2ln2.
Câu 49:
Trong không gian Oxyz, cho điểm A(1; 2; −1), đường thẳng d: và mặt phẳng (P): x + y + 2z + 1 = 0. Điểm B thuộc (P) thỏa mãn đường thẳng AB vuông góc và cắt d. Tọa độ của B là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đường thẳng d: có một vectơ chỉ phương là = (2; 1; −1)
Gọi M = AB ∩ d
Þ M(1 + 2t; −1 + t; 2 – t)
Với A(1; 2; −1) ta có:
= (2t; t – 3; 3 – t)
Lại có AB ^ d Û . = 0
Û 2.2t + 1.(t – 3) – 1.(3 – t) = 0
Û 4t + t – 3 – 3 + t = 0
Û t = 1
Þ
Þ = (1; −1; 1)
Đường thẳng AB đi qua điểm A(1; 2; −1) có vectơ chỉ phương = (1; −1; 1) có phương trình là:
(t ∈ ℝ)
B nằm trên AB nên ta có B(1 + t'; 2 – t'; –1 + t')
Do B = AB ∩ (P) nên tọa độ của B thỏa mãn phương trình của (P): x + y + 2z + 1 = 0.
Þ 1 + t' + 2 – t' + 2.(–1 + t') + 1 = 0
Þ 2t' + 2 = 0
Þ t' = –1
Khi đó B(0; 3; −2)
Vậy tọa độ của B là (0; 3; −2).
Câu 50:
Trong không gian Oxyz, cho điểm M(1; 2; 3) và đường thẳng d: . Mặt phẳng đi qua M và chứa d có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường thẳng d: có vectơ chỉ phương = (2; 1; −1) và đi qua điểm M(1; 2; 3)
Lấy điểm H(1; 1; 1) ∈ d
Þ = (0; −1; −2)
Với = (2; 1; −1) và = (0; −1; −2) ta có :
[; ] = (−3; 4; −2)
Gọi (P) là mặt phẳng cần tìm, ta có (P) chứa d và M nên (P) có vectơ pháp tuyến cùng phương với [; ] = (−3; 4; −2)
Do đó = (3; −4; 2)
(P) có = (3; −4; 2) và đi qua M(1; 2; 3) có phương trình là:
3(x – 1) − 4(y – 2) + 2(z – 3) = 0
Û 3x – 3 – 4y + 8 + 2z – 6 = 0
Û 3x − 4y + 2z – 1 = 0
Vậy phương trình (P) cần tìm là 3x – 4y + 2z – 1 = 0.
