38 câu hỏi trắc nghiệm thuộc Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 4

Câu 1:

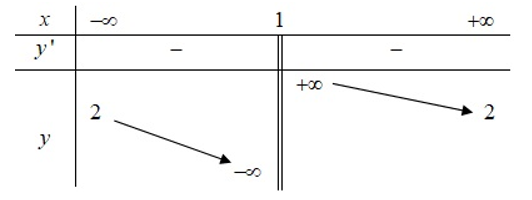
Cho hàm số $y = f (x)$ xác định và liên tục trên khoảng R có bảng biến thiên như hình sau:

.

A. Hàm số nghịch biến trên khoảng

(1; + \infty)

.

B. Hàm số đồng biến trên khoảng

(- \infty; - 1)

.

C. Hàm số nghịch biến trên khoảng

(- \infty; 1)

.

D. Hàm số đồng biến trên khoảng

(- 1; + \infty)

.

Xem đáp án

Chọn B

Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng $(- \infty; - 1)$

Câu 2:

Cho hàm số y=f(x) xác định và liên tục trên khoảng R có đồ thị như hình sau:

Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng

(1; 5)

B. Hàm số đồng biến trên khoảng

(1; 2)

.

C. Hàm số nghịch biến trên khoảng

(1; 2)

D. Hàm số đồng biến trên khoảng

(1; 5)

.

Xem đáp án

Chọn B.

Từ đồ thị ta có đáp án.

Câu 3:

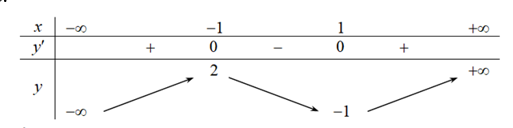
Cho hàm số $y = f (x)$ xác định và liên tục trên khoảng R có bảng xét dấu đạo hàm như hình sau:

Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng

(2; + \infty)

B. Hàm số nghịch biến trên khoảng

(- \infty; - 2)

C. Hàm số nghịch biến trên khoảng

(- 2; 2)

D. Hàm số nghịch biến trên khoảng

(- 2; + \infty)

.

Xem đáp án

Chọn B.

Ta có bảng biến thiên:

Cho hàm số y=f(x) xác định và liên tục trên khoảng R có bảng xét dấu đạo hàm như hình sau: (ảnh 2)

Từ bảng biến thiên ta thấy hàm số nghịch biến trên khoảng $(- \infty; - 2)$

Câu 4:

Cho hàm số

y = f (x)

xác định và liên tục trên

(a; b)

(có thể a là

- \infty; b

là

+ \infty)

và điểm

x_{0} \in (a; b) .

Nếu tồn tại số

h > 0

sao cho

f (x) < f (x_{0})

với mọi

x \in (x_{0} - h; x_{0} + h)

và

x \neq x_{0}

thì ta nói:

A. Hàm số

f (x)

đạt cực đại tại

x_{0} .

B. Hàm số

f (x)

đạt cực tiểu tại

x_{0} .

C. Đồ thị hàm số

f (x)

đạt cực đại tại

x_{0} .

D. Đồ thị hàm số

f (x)

đạt cực tiểu tại

x_{0} .

Xem đáp án

Chọn A

Lý thuyết sách giáo khoa.

Câu 5:

Cho hàm số $y = f (x)$ đạt cực tiểu tại $x_{0} .$ Khi đó mệnh đề nào sau đây sai

A. $x_{0} .$ được gọi là điểm cực tiểu của hàm số.

B. $f (x_{0})$ được gọi giá trị cực tiểu của hàm số.

C. Điểm

M (x_{0}; f (x_{0}))

được gọi là cực tiểu của đồ thị hàm số.

D. Đồ thị hàm số

f (x)

đạt cực tiểu tại

x_{0} .

Xem đáp án

Chọn D

Lý thuyết sách giáo khoa.

Câu 6:

Giả sử hàm số $y = f (x)$ liên tục trên khoảng $K = (x_{0} - h; x_{0} + h)$ và có đạo hàm trên K hoặc trên $K \ \{x_{0}\},$ với $h > 0.$ Mệnh đề nào sau đây đúng:

A. Nếu

f' (x) > 0

trên khoảng

(x_{0} - h; x_{0})

và

f' (x) < 0

trên khoảng

(x_{0}; x_{0} + h)

thì

x_{0}

là một điểm cực đại của hàm số.

B. Nếu

f' (x) < 0

trên khoảng

(x_{0} - h; x_{0})

và

f' (x) > 0

trên khoảng

(x_{0}; x_{0} + h)

thì

x_{0}

là một điểm cực đại của hàm số.

C. Nếu

f' (x) = 0

trên khoảng

(x_{0} - h; x_{0})

và

f' (x) < 0

trên khoảng

(x_{0}; x_{0} + h)

thì

x_{0}

là một điểm cực đại của hàm số.

D. Nếu

f' (x) > 0

trên khoảng

(x_{0} - h; x_{0})

và

f' (x) = 0

trên khoảng

(x_{0}; x_{0} + h)

thì

x_{0}

là một điểm cực đại của hàm số.

Xem đáp án

Chọn A

Lý thuyết sách giáo khoa.

Câu 7:

Cho hàm số $y = f (x)$ có đạo hàm trên R. Cho các mệnh đề sau:

E: “Nếu đạo hàm đổi dấu khi x chạy qua $x_{0}$ thì hàm số đạt cực tiểu tại $x_{0}$ ”.

F: “Nếu $f^{'} (x_{0}) = 0$ thì hàm số đạt cực trị tại $x_{0}$ ”.

G: “Nếu hàm số đạt cực trị tại $x_{0}$ thì đạo hàm đổi dấu khi x chạy qua $x_{0}$ ”.

H: “Nếu $f^{'} (x_{0}) = f^{''} (x_{0}) = 0$ thì hàm số không đạt cực trị tại $x_{0}$ ”.

Có bao nhiêu mệnh đề sai?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn C

Theo các định lý đã học: Các mệnh đề: E, F, H: sai; mệnh đề: G: đúng.

Do đó có mệnh đề sai.

Câu 8:

Hàm số

y = f (x)

xác định trên D. Trong các mệnh đề sau mệnh đề nào sai?

A. $m = \min_{D} f (x)$ nếu

f (x) \geq m

với mọi

x \in D

và tồn tại

x_{0} \in D

sao cho

f (x_{0}) = m .

B. $m = \min_{D} f (x)$ nếu

f (x) \geq m

với mọi

x \in D

.

C. Nếu

m = \min_{D} f (x)

thì tồn tại

x_{0} \in D

sao cho

f (x_{0}) = m .

D. Nếu

m = \min_{D} f (x)

thì

f (x) \geq m

với mọi

x \in D

.

Xem đáp án

Chọn B

Theo khái niệm GTNN của hàm số ta thấy mệnh đề sai là: “ $m = \min_{D} f (x)$ nếu $f (x) \geq m$ với mọi $x \in D$ ”.

Câu 9:

Hàm số

y = f (x)

xác định trên . Trong các mệnh đề sau mệnh đề nào đúng?

A. $M = \max_{D} f (x)$ nếu

f (x) < M

với mọi

x \in D

B. $M = \max_{D} f (x)$ nếu

f (x) \leq M

với mọi

x \in D

.

C. $M = \max_{D} f (x)$ nếu

f (x) \leq M

với mọi

x \in D

và tồn tại

x_{0} \in D

sao cho

f (x_{0}) = M .

D. Nếu

M = \max_{D} f (x)

thì

f (x) < M

với mọi

x \in D

.

Xem đáp án

Chọn C

Theo khái niệm GTLN của hàm số ta thấy mệnh đề đúng là sai là: “ $M = \max_{D} f (x)$ nếu $f (x) \leq M$ với mọi $x \in D$ và tồn tại $x_{0} \in D$ sao cho $f (x_{0}) = M .$ ”.

Câu 10:

Đồ thị hàm số nào dưới đây có dạng như hình bên?

A. $y = x^{3} - 3 x$

B. $y = - x^{3} + 3 x$

C. $y = x^{4} - 2 x^{2}$

D. $y = - x^{4} + 2 x^{2}$

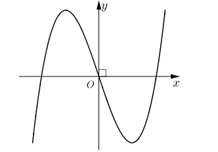
Xem đáp án

Chọn A

Nhìn vào đồ thị ta thấy hệ số a>0 và là hàm số bậc 3 nên ta chọn đáp án A .

Câu 11:

Đồ thị hàm số nào dưới đây có dạng như hình bên?

A. $y = x^{3} - 3 x^{2} - 2$

B. $y = - x^{3} + 3 x^{2} - 2$

C. $y = x^{4} - 2 x^{2} - 2$

D. $y = - x^{4} + 2 x^{2} - 2$

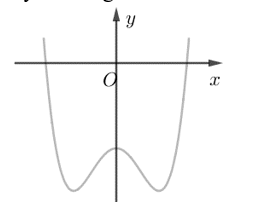
Xem đáp án

Chọn C

Nhìn vào đồ thị ta thấy hệ số $a > 0$ và là hàm số bậc 4 nên ta chọn đáp án C.

Câu 12:

Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = \frac{1 - x}{3 x + 2}$ là

A. $y = \frac{1}{3}; x = - \frac{2}{3}$

B. $y = - \frac{1}{3}; x = - \frac{2}{3}$

C. $y = - \frac{2}{3}; x = \frac{1}{3}$

D. $y = \frac{2}{3}; x = - \frac{1}{3}$

Xem đáp án

Chọn B

Đồ thị hàm số $y = \frac{1 - x}{3 x + 2}$ có TCN,TCĐ lần lượt là $y = - \frac{1}{3}; x = - \frac{2}{3}$ .

Câu 13:

Đường thẳng $x = x_{0}$ được gọi là đường tiệm cận đứng của đồ thị hàm số y=f(x) nếu

A. Hàm số không xác định tại điểm .

x_{0}

B. $\lim_{x \to + \infty} f (x) = x_{0}$

C. $\lim_{x \to {x_{0}}^{+}} f (x) = + \infty$

D. $\lim_{x \to {x_{0}}^{+}} f (x) = 0$

Xem đáp án

Chọn C

Câu 14:

Cho hàm số y=f(x) liên tục trên $ℝ \ \{1\}$ có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y=f(x)

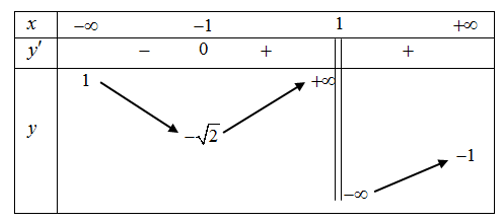
$Cho hàm số y=f(x) liên tục trên R\{1} có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y=f(x) (ảnh 1)$

A. 1

B. 4

C. 2

D. 3

Xem đáp án

Chọn D

Do $\lim_{x \to 1^{+}} y = - \infty; \lim_{x \to 1^{-}} = + \infty \Leftrightarrow$ TCĐ: $x = 1.$

$\lim_{x \to + \infty} y = - 1; \lim_{x \to - \infty} y = 1 \Rightarrow$ đồ thị có 2 tiệm cận ngang là $y = \pm 1$

Vậy, đồ thị hàm số đã cho có tổng số TCĐ và TCN là 3.

Câu 15:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.

B. Số đỉnh và số mặt của một hình đa diện luôn bằng nhau.

C. Tồn tại một hình đa diện có số cạnh và số mặt bằng nhau.

D. Tồn tại một hình đa diện có số cạnh bằng số đỉnh

Xem đáp án

Chọn A

Hình tứ diện có số đỉnh bằng số mặt và bằng bốn.

Câu 16:

Khối đa diện đều loại $\{4; 3\}$ có số đỉnh là

A. 10

B. 8

C. 4

D. 6

Xem đáp án

Chọn B

Khối đa diện đều loại $\{4; 3\}$ là hình lập phương nên có 8 đỉnh.

Câu 17:

Thể tích khối lăng trụ có chiều cao h và diện tích đáy S là

A. Sh

B. $\frac{1}{6} S h .$

C. $\frac{1}{3} S h .$

D. $\frac{1}{2} S h .$

Xem đáp án

Chọn D

Câu 18:

Một khối lăng trụ đứng có diện tích đáy bằng $6 a^{2}$ và độ dài cạnh bên bằng 2a thì thể tích của khối lăng trụ đó bằng

A. $V = 4 a^{3}$

B. $V = 12 a^{3} .$

C. $V = 6 a^{3}$

D. $V = a^{3} .$

Xem đáp án

Chọn B

Tính thể tích khối lăng trụ: $V = B h = 6 a^{2} .2 a = 12 a^{3} .$

Câu 19:

Cho hình chóp SABC có đáy ABC là tam giác vuông tại $B, A B = a, B C = 2 a,$ $S A ⊥ (A B C)$ và $S A = a \sqrt{3} .$ Thể tích khối chóp SABC bằng

A. $V = \frac{a^{3} \sqrt{3}}{6} .$

B. $V = a^{3} \sqrt{3} .$

C. $V = \frac{a^{3} \sqrt{3}}{2} .$

D. $V = \frac{a^{3} \sqrt{3}}{3} .$

Xem đáp án

Chọn D

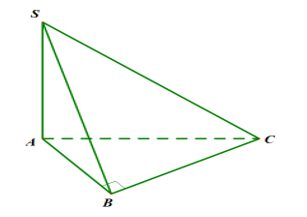
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a, SA vuông góc ( ABC) và SA= a căn 3 Thể tích khối chóp SABC bằng (ảnh 1)

Ta có: $+ S_{A B C} = \frac{1}{2} . B A . B C = \frac{1}{2} . a .2 a = a^{2} .$

Thể tích khối chóp : $V_{S A B C} = \frac{1}{3} S A . S_{A B C} = \frac{1}{3} a \sqrt{3} . a^{2} = \frac{a^{3} \sqrt{3}}{3} .$

Câu 20:

Cho hàm số $y = f (x)$ biết $f^{'} (x) = x^{2} (x - 1) {(2 - x)}^{3} .$ Hỏi hàm số $y = f (x)$ đồng biến trên khoảng nào?

A. $(1; 2) .$

B. $(0; 2) .$

C. $(1; + \infty) .$

D. $(- \infty; 1) .$

Xem đáp án

Chọn A

Ta có: $f^{'} (x) = 0 \Leftrightarrow x^{2} (x - 1) {(2 - x)}^{3} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 1 \\ x = 2 \end{array}$

Bảng xét dấu của $f^{'} (x)$

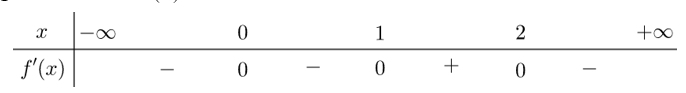
Cho hàm số y=f(x) biết f'(x)=x^2( x-1)( 2-x)^3 Hỏi hàm số đồng biến trên khoảng nào? (ảnh 1)

Từ bảng xét dấu của $f^{'} (x)$ hàm số đồng biến trên khoảng $(1; 2) .$

Câu 21:

Cho hàm số $y = f (x)$ có đạo hàm trên K ( Klà một khoảng, đoạn hoặc nửa khoảng).

Khẳng định nào sau đây đúng?

A. Nếu

f^{'} (x) \geq 0, \forall x \in K

thì hàm số

f (x)

đồng biến trên K

B. Nếu

f^{'} (x) > 0, \forall x \in K

thì hàm số

f (x)

nghịch biến trên K

C. Nếu

f^{'} (x) > 0, \forall x \in K

thì hàm số

f (x)

đồng biến trên K

D. Nếu

f^{'} (x) \leq 0, \forall x \in K

thì hàm số

f (x)

nghịch biến trên K

Xem đáp án

Chọn C

Câu 22:

Tìm m để hàm số $y = x^{3} - 3 m x^{2} + 3 (2 m - 1) x - 2$ có cực trị.

A. $m > 1.$

B. $m \geq 1.$

C. $m \leq 1.$

D. $m \neq 1.$

Xem đáp án

Chọn D

$y = x^{3} - 3 m x^{2} + 3 (2 m - 1) x - 2 \Rightarrow y^{'} = 3 x^{2} - 6 m x + 3 (2 m - 1) .$

Hàm số $y = x^{3} - 3 m x^{2} + 3 (2 m - 1) x - 2$ có cực trị khi và chỉ khi $y^{'} = 0$ có 2 nghiệm phân biệt

$\Leftrightarrow Δ^{'} > 0 \Leftrightarrow {(- 3 m)}^{2} - 3.3. (2 m - 1) > 0 \Leftrightarrow 9 m^{2} - 18 m + 9 > 0 \Leftrightarrow m \neq 1.$

Câu 23:

Cho hàm số $y = x^{4} - x^{2} + 1.$ Khẳng định nào sau đây đúng?

A. Hàm số có 1 điểm cực đại và 2 điểm cực tiểu

B. Hàm số có 2 điểm cực đại và 1 điểm cực tiểu.

C. Hàm số có 1 điểm cực trị.

D. Hàm số có 2 điểm cực trị.

Xem đáp án

Chọn A

Hàm số $y = x^{4} - x^{2} + 1$ có $y' = 4 x^{3} - 2 x = 2 x (2 x^{2} - 1) \Rightarrow y^{'} = 0$ có 3 nghiệm phân biệt

$x_{1} = - \frac{\sqrt{2}}{2}; x_{2} = 0; x_{3} = \frac{\sqrt{2}}{2} .$

Bảng biến thiên

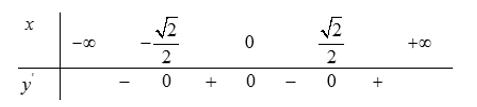
Cho hàm số y= x^4-x^2+1 Khẳng định nào sau đây đúng? (ảnh 1)

Vậy hàm số $y = x^{4} - x^{2} + 1$ có điểm cực đại và điểm cực tiểu.

Câu 24:

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{1}{3} x^{3} - 2 x^{2} + 3 x - \frac{1}{3}$ trên đoạn $[0; 2]$ . Tính tổng $S = M + m$ .

A. $S = \frac{1}{3}$

B. $S = \frac{4}{3}$

C. $S = 1$

D. $S = \frac{2}{3}$

Xem đáp án

Chọn D

TXĐ: D=R.

$y^{'} = x^{2} - 4 x + 3 \Rightarrow y^{'} = 0 \Leftrightarrow [\begin{matrix} x = 1 \\ x = 3 \end{matrix}$ . Với $x \in [0; 2]$ thì $x = 1$ thỏa mãn.

Ta có: $f (0) = - \frac{1}{3}, f (1) = 1, f (2) = \frac{1}{3}$ .

Vậy M=1 và $m = - \frac{1}{3} \Rightarrow S = 1 - \frac{1}{3} = \frac{2}{3}$ .

Câu 25:

Giá trị lớn nhất của hàm số $y = - 3 x^{4} + 4 x^{3} + 1$ bằng

A. 11

B. 0

C. 5

D. 2

Xem đáp án

Chọn D

Tập xác định: $D = (- \infty; + \infty)$

Ta có $y^{'} = - 12 x^{3} + 12 x^{2} \Rightarrow y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 1 \end{array}$ (x=0 là nghiệm kép).

Khi đó ta có bảng biến thiên:

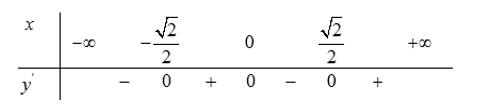
Giá trị lớn nhất của hàm số y= -3x^4+4x^3+1 bằng (ảnh 1)

Dựa vào bảng biến thiên giá trị lớn nhất của hàm số bằng 2 .

Câu 26:

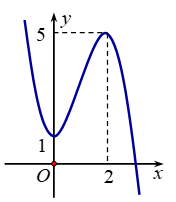
Đường cong trong hình bên là đồ thị của hàm số nào sau đây?

A. $y = x^{3} - 3 x^{2} + 1$

B. $y = 2 x^{4} - 4 x^{2} + 1$

C. $y = - 2 x^{4} + 4 x^{2} + 1$

D. $y = - 2 x^{4} + 4 x^{2}$

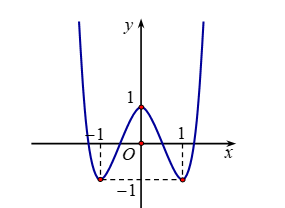
Xem đáp án

Chọn B

Đồ thị đã cho là đồ thị hàm trùng phương có hệ số $a > 0$ và đi qua điểm $(0; 1) \Leftrightarrow$ loại A, C, D

Vậy đó là đồ thị hàm số $y = 2 x^{4} - 4 x^{2} + 1$ .

Câu 27:

Cho hàm số $y = f (x)$ có đồ thị như hình bên

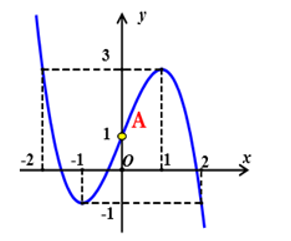
Khi đó phương trình tiếp tuyến của đồ thị hàm số tại điểm A trên hình vẽ là

A. $y = 3 x + 1$

B. $y = 3 x - 1$

C. $y = 3 x + 2$

D. $y = 3 x - 2$

Xem đáp án

Chọn A

Giả sử hàm số cần là: $y = a x^{3} + b x^{2} + c x + d, (a \neq 0)$

Ta có: $y^{'} = 3 a x^{2} + 2 b x + c$ .

Theo giả thiết ta có:

$\{\begin{cases} f (- 2) = 3 \\ f (- 1) = - 1 \\ f (1) = 3 \\ f (0) = 1 \end{cases} \Leftrightarrow \{\begin{cases} - 8 a + 4 b - 2 c = 2 \\ - a + b - c = - 2 \\ a + b + c = 2 \\ d = 1 \end{cases} \Leftrightarrow (\begin{array}{l} a = - 1 \\ b = 0 \\ c = 3 \\ d = 1 \end{array}$ .

$\Rightarrow y = - x^{3} + 3 x + 1 \Rightarrow y^{'} = - 3 x^{2} + 3 \Rightarrow y^{'} (0) = 3$

Phương trình tiếp tuyến tại

A (0; 1)

là:

y = f' (0) . (x - 0) + y (0) \Leftrightarrow y = 3 x + 1

.

Câu 28:

Cho hàm số $f (x)$ liên tục trên R và có bảng biến thiên như sau:

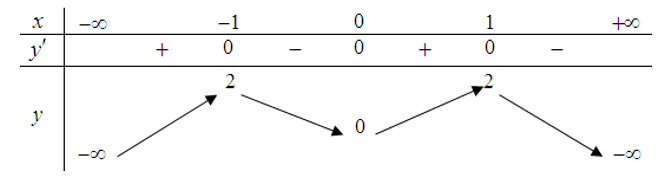
Số nghiệm thuộc khoảng $(- \infty; \ln 2)$ của phương trình $2019 f (1 - e^{x}) - 2021 = 0$ là

A. 1

B. 3

C. 2

D. 1

Xem đáp án

Chọn C

Đặt $t = 1 - e^{x}$ ; $x \in (- \infty; \ln 2)$ $\Rightarrow t \in (- 1; 1)$ .

Nhận xét: $x = \ln (1 - t)$ $\Rightarrow$ với mỗi giá trị của $t \in (- 1; 1)$ ta được một giá trị của $x \in (- \infty; \ln 2)$ .

Phương trình tương đương: $f (t) = \frac{2021}{2019}$ .

Sử dụng bảng biến thiên của $f (x)$ cho $f (t)$ như sau:

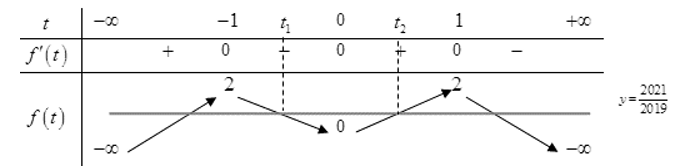
Cho hàm số f(x) liên tục trên R và có bảng biến thiên như sau: Số nghiệm thuộc khoảng ( - vô cùng, ln2) của phương trình 2019f(1-e^x) -2021=0 là (ảnh 2)

Dựa vào bảng biến thiên ta thấy phương trình $f (t) = \frac{2021}{2019}$ có 2 nghiệm $t_{1}, t_{2} \in (- 1; 1)$ .

Vậy phương trình $2019 f (1 - e^{x}) - 2021 = 0$ có 2 nghiệm $x \in (- \infty; \ln 2)$ .

Câu 29:

Tìm số tiệm cận của đồ thị hàm số $y = \frac{x^{2} - 5 x + 4}{x^{2} - 1}$ .

A. 2

B. 3

C. 0

D. 1

Xem đáp án

Chọn A

Tập xác định: $D = ℝ \ \{\pm 1\}$

Ta có: $\lim_{x \to \pm \infty} y = \lim_{x \to \pm \infty} \frac{x^{2} - 5 x + 4}{x^{2} - 1} = \lim_{x \to \pm \infty} \frac{1 - \frac{5}{x} + \frac{4}{x^{2}}}{1 - \frac{1}{x^{2}}} = 1$ $\Rightarrow y = 1$ là đường tiệm cận ngang.

Mặc khác: $\lim_{x \to 1^{}} y = \lim_{x \to 1^{}} \frac{x^{2} - 5 x + 4}{x^{2} - 1} = \lim_{x \to 1} \frac{(x - 1) (x - 4)}{(x - 1) (x + 1)} = \lim_{x \to 1} \frac{(x - 4)}{(x + 1)} = - \frac{3}{2}$

$\Rightarrow x = 1$ không là đường tiệm cận đứng.

$\lim_{x \to {(- 1)}^{+}} y = \lim_{x \to {(- 1)}^{+}} \frac{x^{2} - 5 x + 4}{x^{2} - 1} = \lim_{x \to 1^{+}} \frac{(x - 1) (x - 4)}{(x - 1) (x + 1)} = \lim_{x \to {(- 1)}^{+}} \frac{(x - 4)}{(x + 1)} = - \infty$

$\lim_{x \to {(- 1)}^{-}} y = \lim_{x \to {(- 1)}^{-}} \frac{x^{2} - 5 x + 4}{x^{2} - 1} = \lim_{x \to {(- 1)}^{-}} \frac{(x - 1) (x - 4)}{(x - 1) (x + 1)} = \lim_{x \to {(- 1)}^{-}} \frac{(x - 4)}{(x + 1)} = + \infty$

$\Rightarrow x = - 1$ là đường tiệm cận đứng.

Vậy đồ thị hàm số có 2 đường tiệm cận.

Câu 30:

Cho hàm số

y = f (x)

có bảng biến thiên như sau. Khẳng định nào sau đây là sai?

A. $x = 1$ là tiệm cận đứng của đồ thị hàm số.

B. $\lim_{x \to 1^{+}} y = - \infty, \lim_{x \to 1^{-}} y = + \infty$

C. $\lim_{x \to - \infty} y = \lim_{x \to + \infty} y = 2$

D. y=2 là tiệm cận ngang của đồ thị hàm số.

Xem đáp án

Chọn B

Câu 31:

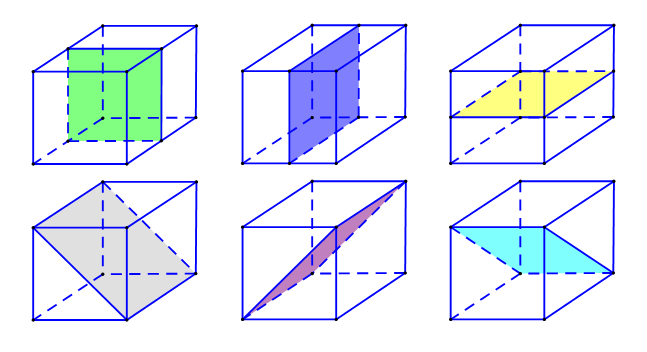
Số mặt phẳng đối xứng của khối đa diện đều $\{4; 3\}$ là:

A. 3

B. 6

C. 9

D. 8

Xem đáp án

Chọn C

Hình lập phương là khối đa diện đều $\{4; 3\}$ . Hình lập phương có 9 mặt phẳng đối xứng:

Số mặt phẳng đối xứng của khối đa diện đều {4,3} là: (ảnh 1)

Câu 32:

Khối đa diện đều nào có số đỉnh nhiều nhất?

A. Khối thập nhị diện đều (12 mặt đều).

B. Khối bát diện đều (8 mặt đều).

C. Khối nhị thập diện đều (20 m)

D. Khối tứ diện đều

Xem đáp án

Chọn A

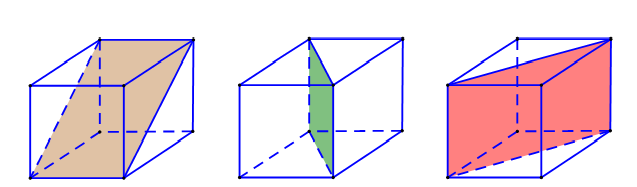
Câu 33:

Cho lăng trụ tam giác đều $A B C . A^{'} B^{'} C^{'}$ có tất cả các cạnh bằng a. Thể tích khối lăng trụ $A B C . A^{'} B^{'} C^{'}$ là :

A. $\frac{a^{3}}{4}$

B. $\frac{a^{3} \sqrt{3}}{12}$

C. $\frac{a^{3}}{12}$

D. $\frac{a^{3} \sqrt{3}}{4}$

Xem đáp án

Chọn D

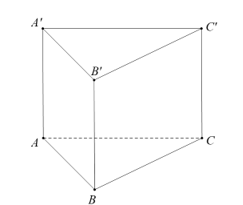
Cho lăng trụ tam giác đều ABCA'B'C' có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABCA'B'C' là : (ảnh 1)

$V_{A B C . A^{'} B^{'} C^{'}} = A A^{'} . S_{Δ A B C} = a . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{3} \sqrt{3}}{4}$

Câu 34:

Khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a. Thể tích của khối chóp đã cho bằng?

A. $16 a^{3}$

B. $\frac{16}{3} a^{3}$

C. $4 a^{3}$

D. $\frac{4}{3} a^{3}$

Xem đáp án

Chọn D

Áp dụng công thức tính thể tích khối chóp $V = \frac{1}{3} . S . h = \frac{1}{3} . a^{2} .4 a = \frac{4}{3} a^{3}$

Câu 35:

Cho hàm số $y = \frac{(4 - m) \sqrt{6 - x} + 3}{\sqrt{6 - x} + m}$ . Tìm giá trị nguyên của m trong khoảng $(1; 5)$ sao cho hàm số đồng biến trên khoảng $(- 10; 5)$ ?

Xem đáp án

Đặt $t = \sqrt{6 - x} \Rightarrow t^{'} = \frac{- 1}{2 \sqrt{6 - x}} < 0, \forall x \in (- 10; 5)$ . Với $x \in (- 10; 5)$ $\Rightarrow t \in (1; 4)$ .

Ta có $f (t) = \frac{(4 - m) t + 3}{t + m} \Rightarrow f^{'} (t) = \frac{- m^{2} + 4 m - 3}{{(t + m)}^{2}}$ .

Từ đó ta suy ra hàm số $y = \frac{(4 - m) \sqrt{6 - x} + 3}{\sqrt{6 - x} + m}$ đồng biến trên khoảng $(- 10; 5)$ khi hàm số $f (t) = \frac{(4 - m) t + 3}{t + m}$

nghịch biến trên khoảng $(1; 4)$ .

$f (t)$ nghịch biến trên khoảng $(1; 4) \Rightarrow$ . $\{\begin{cases} - m^{2} + 4 m - 3 < 0 \\ [\begin{array}{l} - m \leq 1 \\ - m \geq 4 \end{array} \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} m < 1 \\ m > 3 \end{array} \\ [\begin{array}{l} m \geq - 1 \\ m \leq - 4 \end{array} \end{cases} \Leftrightarrow [\begin{array}{l} - 1 \leq m < 1 \\ m > 3 \\ m \leq - 4 \end{array}$

Do $m \in (1; 5)$ nên $m = 4.$

Vậy $m = 4.$

Câu 36:

Cho hình lập phương ABCDA'B'C'D' cạnh a bằng $K \in C C^{'}$ sao cho $C K = \frac{2}{3} a$ . Mặt phẳng (α) qua A,K và song song với BD chia khối lập phương trình hai phần. Tính tỷ số thể tích hai phần đó.

Xem đáp án

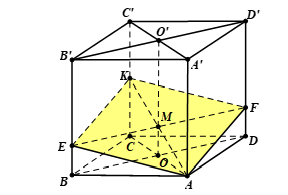
Cho hình lập phương ABCDA'B'C'D' cạnh a bằng K thuộc CC' sao cho CK= 2/3a . Mặt phẳng (α) qua A,K và song song với BD chia khối lập phương (ảnh 1)

Gọi $O, O^{'}$ là tâm của hình vuông $A B C D . A^{'} B^{'} C^{'} D^{'}$ , $M = A K \cap .$

Qua M kẻ đường thẳng song song với BD cắt $B B ’, D D ’$ lần lượt tại E,F

Khi đó, thiết diện tạo bởi (α) và hình lập phương chính là hình bình hành AEKF.

Có OM là đường trung bình tam giác ACK nên $O M = \frac{1}{2} C K = \frac{a}{3} .$

Do đó, $B E = D F = \frac{1}{2} C K = \frac{a}{3}$ . Đặt $V_{1} = V_{A B E K F D C}, V_{2} = V_{A E K F A^{'} B^{'} C^{'} D^{'}} .$

Ta có hai tứ giác bằng nhau: $B C K E = C^{'} B^{'} E K,$ mặt phẳng $(A A^{'} C^{'} C)$ chia khối $A B E K F D C$ thành hai phần bằng nhau nên: $\begin{array}{l} V_{1} = 2 V_{A . B C K E} = 2. \frac{1}{3} . A B . S_{B C K E} = \frac{2}{3} a . \frac{1}{2} . S_{B C C^{'} B^{'}} = \frac{a^{3}}{3} . \\ V_{2} = V_{A B C D . A^{'} B^{'} C^{'} D^{'}} - V_{1} = a^{3} - \frac{a^{3}}{3} = \frac{2 a^{3}}{3} . \end{array}$

Vậy $\frac{V_{1}}{V_{2}} = \frac{1}{2} .$

Câu 37:

Một người cần đi từ khách sạnA bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là $5 USD/km$ , đi đường bộ là $3 USD/km$ . Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất? ( $A B = 40 km$ , $B C = 10 km$ )

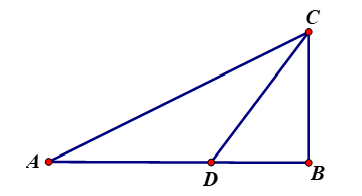
Một người cần đi từ khách sạnA bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách (ảnh 1)

Xem đáp án

Đặt $A D = x km$ , $x \in [0; 40] \Rightarrow B D = 40 - x \Rightarrow C D = \sqrt{{(40 - x)}^{2} + 10^{2}}$ .

Tổng kinh phí đi từ A đến C là $f (x) = x .3 + \sqrt{{(40 - x)}^{2} + 10^{2}} .5$ .

$f (x) = 3 x + 5 \sqrt{x^{2} - 80 x + 1700}$ .

$f^{'} (x) = 3 + 5 \frac{2 x - 80}{2 \sqrt{x^{2} - 80 x + 1700}} \Leftrightarrow f^{'} (x) = \frac{3 \sqrt{x^{2} - 80 x + 1700} + 5 x - 200}{\sqrt{x^{2} - 80 x + 1700}}$ .

$f^{'} (x) = 0 \Leftrightarrow 3 \sqrt{x^{2} - 80 x + 1700} = 200 - 5 x \Leftrightarrow x = \frac{65}{2}$ .

Bảng biến thiên

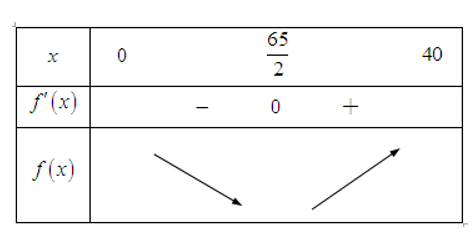
Một người cần đi từ khách sạnA bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách (ảnh 2)

Dựa vào bảng biến thiên, ta thấy hàm đạt giá trị nhỏ nhất tại $x = \frac{65}{2}$

Câu 38:

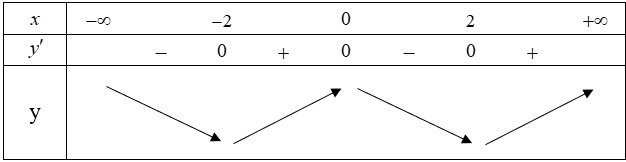
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y = |3 x^{4} - 4 x^{3} - 12 x^{2} + m|$ có 5 điểm cực trị.

Xem đáp án

Đặt: $g (x) = 3 x^{4} - 4 x^{3} - 12 x^{2} + m$

Ta có: $g' (x) = 12 x^{3} - 12 x^{2} - 24 x = 0 \Leftrightarrow [\begin{array}{l} x = 2 \Rightarrow y = m - 32 \\ x = - 1 \Rightarrow y = m - 5 \\ x = 0 \Rightarrow y = m \end{array}$

Dựa vào bảng biến thiên, hàm số có có $y = |g (x)|$ điểm cực trị khi $[\begin{array}{l} m < 0 \\ \{\begin{cases} m - 5 > 0 \\ m - 32 < 0 \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} m < 0 \\ 5 < m < 32 \end{array}$ . Vì m là số nguyên dương cho nên có 26 số m thỏa đề bài