Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 18
-
4386 lượt thi
-
50 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
Cho hàm số liên tục trên R và có đạo hàm Hỏi hàm số có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Chọn D
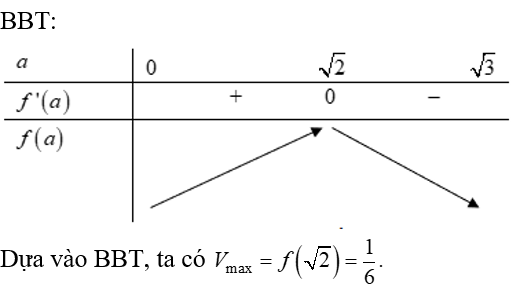
Bảng biến thiên:
Dựa vào BBT ta thấy hàm số có 2 điểm cực trị.
Câu 3:
Cho hàm số liên tục trên R . Hàm số có đồ thị như hình vẽ:
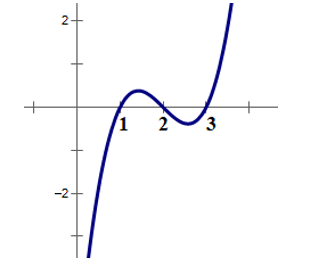
Khẳng định nào sau đây ĐÚNG?
 Xem đáp án
Xem đáp án
Chọn D
Ta thấy đồ thị cắt trục Ox tại 3 điểm phân biệt nên có 3 nghiệm đơn phân biệt.
Do đó đồ thị hàm số có 3 điểm cực trị.
Câu 4:
Số đường tiệm cận của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Chọn C
Ta có: TXĐ
Đồ thị hàm số có 1 tiệm cận ngang .
Đồ thị hàm số có tiệm cận đứng x=2 .
Đồ thị hàm số có tiệm cận đứng x=-2
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 6:
Cho hàm số . Khẳng định nào sau đây là ĐÚNG?
 Xem đáp án
Xem đáp án
Chọn D
Ta có: .
Vậy hàm số luôn nghịch biến trên R .
Câu 7:
Điểm cực tiểu của đồ thị hàm số là điểm . Tính tổng
 Xem đáp án
Xem đáp án
Chọn B
Ta có
Bảng biến thiên:
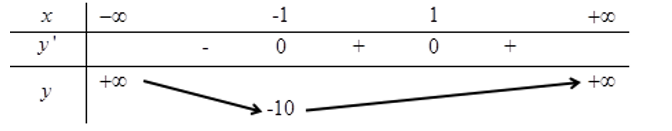
Từ BBT, đồ thị hàm số có điểm cực tiểu là điểm
Vậy
Câu 8:
Tổng các giá trị nhỏ nhất và giá trị lớn nhất của hàm số bằng
 Xem đáp án
Xem đáp án
Chọn A
Điều kiện:
TXĐ:
Hàm số liên tục trên
thì
Ta có:
Do đó
Vậy tổng các giá trị nhỏ nhất và giá trị lớn nhất của hàm số bằng
Câu 9:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số luôn nghịch biến trên R
 Xem đáp án
Xem đáp án
Chọn C
Hàm số luôn nghịch biến trên R
và dấu bằng xảy ra tại hữu hạn điểm trên R
Vậy các giá trị m cần tìm là
Câu 10:
Số đường tiệm cận đứng của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Chọn D
TXĐ:
ta có:
Do đó:
Mặt khác,
Nên đồ thị hàm số đã cho chỉ có một tiệm cận đứng là đường thẳng
Câu 11:
Hàm số nghịch biến trong khoảng nào?
 Xem đáp án
Xem đáp án
Chọn D
TXĐ:
;
BBT
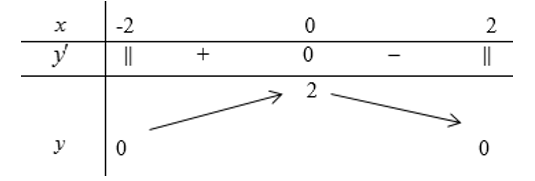
Hàm số nghịch biến trên khoảng (0,2)
Câu 12:
Cho hàm số có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn A
Dựa vào bảng biến thiên ta có: Hàm số đạt cực đại tại và đạt cực tiểu tại x=4
Câu 13:
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
 Xem đáp án
Xem đáp án
Chọn C
Ta có ; nên đồ thị hàm số có tiệm cận đứng .
, nên đồ thị hàm số có tiệm cận ngang .
Câu 14:
Giả sử M ,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên . Khi đó bằng bao nhiêu ?
 Xem đáp án
Xem đáp án
Chọn D
Hàm số liên tục trên .
Ta có ; .
; ; .
Suy ra , .
Do đó .
Câu 15:
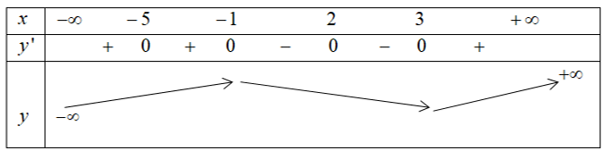
Cho hàm số y=f(x) có bảng biến thiên dưới đây. Khẳng định nào sau đây là khẳng định sai?
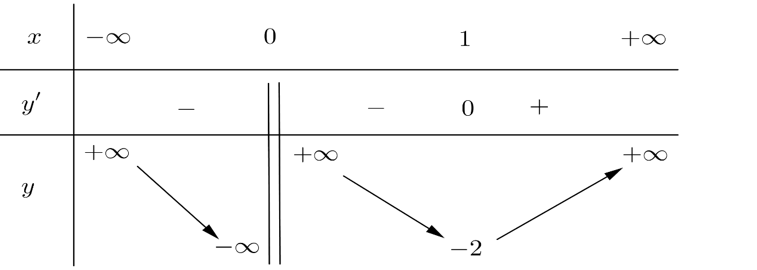
 Xem đáp án
Xem đáp án
Chọn C
Dựa vào bảng biến thiên ta có:
-Hàm số đồng biến trên khoảng ; hàm số nghịch biến trên khoảng và .
Nên đáp án A,B,D đúng và đáp án C sai.
Câu 16:
Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập hợp . Tính giá trị ?
 Xem đáp án
Xem đáp án
Chọn B
Xét hàm số trên
Ta có: .
Bảng biến thiên:
![Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= căn x^2-1/ x-2 trên tập hợp D= (- vô cùng,1) hợp [1, 3/2] . Tính giá trị P= M+m? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/02/blobid4-1676905953.png)
Dựa vào bảng biến thiên ta có: . Vậy .
Câu 17:
Gọi S là tập hợp các giá trị nguyên của tham số m sao cho hàm số nghịch biến trên khoảng . Tính tổng của các m giá trị của S .
 Xem đáp án
Xem đáp án
Chọn B
Tập xác định:
Để hàm số nghịch biến trên khoảng thì
Như vậy .
Câu 18:
Cho hàm số có đạo hàm liên tục trên R . Bảng biến thiên của hàm số được cho như hình vẽ.
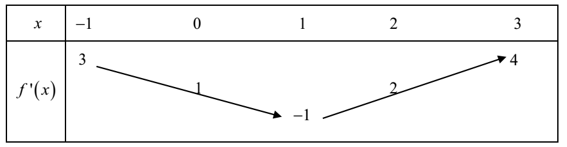
Hàm số nghịch biến trên khoảng nào ?
 Xem đáp án
Xem đáp án
Chọn A
Ta có:
Hàm số nghịch biến
.
Câu 19:
Có bao nhiêu giá trị nguyên sao cho đồ thị của hàm số có hai tiệm cận ngang.
 Xem đáp án
Xem đáp án
Chọn A
Hàm số có hai tiệm cận ngang khi tồn tại hai giới hạn hữu hạn sau:
Với . Đồ thị hàm số là một đường thẳng, không thỏa mãn điều kiện.
Với . Đồ thị hàm số có hai tiệm cân ngang .
Với . Đồ thị hàm số có hai tiệm cân ngang .
Câu 20:
Có bao nhiêu giá trị nguyên của tham số m để hàm số luôn nghịch biến trên từng khoảng xác định của hàm số.
 Xem đáp án
Xem đáp án
Chọn B
Tập xác định .
Yêu cầu bài toán
Với điều kiện thìCâu 21:
Gọi S là tập giá trị m là các số nguyên để hàm số đạt cực trị tại hai điểm thỏa mãn Tính tổng P của các giá trị nguyên của
 Xem đáp án
Xem đáp án
Chọn A
Ta có
Hàm số đạt cực trị tại hai điểm khi có hai nghiệm phân biệt
có hai nghiệm phân biệt.
( luôn đúng với mọi m )
Do đó, với mọi m thì hàm số luôn có hai điểm cực trị .
Theo định lý vi-et ta có
Theo giả thiết :
.
Mà
Câu 22:
Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển Trên bờ biển có một cái kho ở vị trí C cách B một khoảng Người canh hải đăng có thể chèo đò từ A đến M vị trí trên bờ biển với vận tốc rồi đi bộ đến C với vận tốc Vị trí điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất ? ( xem hình vẽ).
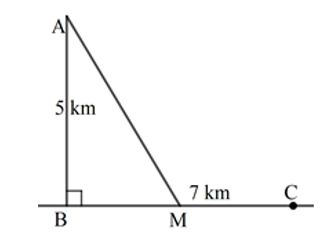
 Xem đáp án
Xem đáp án
Chọn B
Đặt
Tam giác ABM vuông tại B , có
Thời gian đi từ A đến M là , thời gian đi từ M đến C là .
Tổng thời gian đi từ A đến C là .
Xét hàm số trên khoảng , có
Phương trình
Câu 23:
Đồ thị hàm số có tọa độ điểm cực tiểu là . Khi đó bằng
 Xem đáp án
Xem đáp án
Chọn B
Ta có .
Theo giả thiết ta suy ra: .
Khi là điểm cực tiểu của hàm số thỏa mãn.
Lúc đó .
Vậy trong trường hợp này
Khi là điểm cực đại của hàm số nên loại.
Câu 24:
 Xem đáp án
Xem đáp án
Chọn C
TH1: là hàm bậc nhất nên không có tiện cận đứng.
TH2: để hàm số không có tiệm cận đứng thì nghiệm của mẫu số củng là nghiệm của tử số nên suy ra: .
Vậy có 3 giá trị của m là: .Câu 25:
Tìm mối liên hệ giữa các tham số a và b sao cho hàm số luôn tăng trên R ?
 Xem đáp án
Xem đáp án
Chọn C
Hàm số luôn tăng trên R nên (dấu “=” xảy ra tại hữu hạn điểm)
.
Câu 26:
Một hình chóp có 100 cạnh có bao nhiêu mặt?
 Xem đáp án
Xem đáp án
Chọn C
Giả sử hình chóp có đáy là đa giác n cạnh, suy ra có n mặt bên và có n cạnh bên. Khi đó tổng số cạnh của hình chóp là
Vậy hình chóp có 50 mặt bên và 1 mặt đáy. Vậy có tất cả là 51 mặt.
Câu 27:
 Xem đáp án
Xem đáp án
Chọn D
Ta cóCâu 28:
Cho hình chóp tứ giác đều SABCD đáy là hình vuông cạnh a cạnh bên hớp với đáy một góc 60 . Gọi M là trung điểm của SC Mặt phẳng qua A,M và song song với BD cắt SB, SD lần lượt tại E và F và chia khối chóp SABCD là hai phần, khối chóp SAEFMF và đa diện . Tính thể tích của khối đa diện ?
 Xem đáp án
Xem đáp án

Mặt phẳng qua A,M và song song với BD đi qua G và cắt SB,SD lần lượt tại E và F ta suy ra . Thiết diện tạo bởi mặt phẳng đó với hình chóp là tứ giác chia khối chóp thành 2 phần: Khối chóp và phần còn lại, đa diện .
Xét tam giác SBD, vì EF song song với BD nên ta có , nên ta có:
. Vì , nên
Câu 30:
Cho hình chóp đều SABC có cạnh đáy bằng a, cạnh bên bằng . Tính theo a thể tích V của khối chóp đã cho
 Xem đáp án
Xem đáp án
Chọn C
Áp dụng công thức: Hình chóp đều SABC có cạnh đáy bẳng a , cạnh bên bằng thì thể tích khối chóp là:
.
Câu 31:
 Xem đáp án
Xem đáp án
Chọn C
.
Câu 32:
 Xem đáp án
Xem đáp án
Chọn C
Dựa vào hình vẽ ta chọn được đáp án C.
Câu 33:
Kim tự tháp Kheops ( Kê-Ốp ) ở Ai Cập được xây dựng vào năm 2500 trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147m , cạnh đáy dài 230m, . Tính thể tích của nó.
 Xem đáp án
Xem đáp án
Chọn A
Kim tự tháp Kheops là một khối chóp tứ giác đều có cạnh đáy dài 230m nên diện tích s của đáy là:
Chiều cao h của kim tự tháp Kheops là:
Thể tích V của kim tự tháp Kheops là:
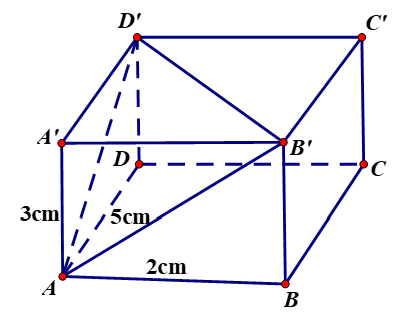
Câu 34:
Một khúc gỗ dạng hình hộp chữ nhật có các kích thước như hình vẽ. Người ta cắt đi một phần khúc gỗ có dạng hình lập phương cạnh bằng 4cm . Tính thể tích phần gỗ còn lại.
 Xem đáp án
Xem đáp án
Chọn B
· Thể tích khối hộp chữ nhật:
· Thể tích khối lập phương:
· Thể tích phần gỗ còn lại:Câu 35:
Tính thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng a và tổng diện tích các mặt bên bằng
 Xem đáp án
Xem đáp án
Chọn C
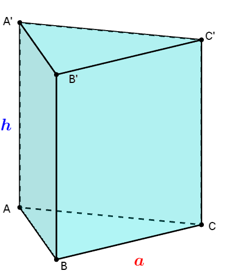
· Khối lăng trụ tam giác đều có cạnh đáy a chiều cao h
· Theo giả thiết;
· Vậy thể tích của khối lăng trụ : (đvtt).
Câu 36:
 Xem đáp án
Xem đáp án
Chọn B
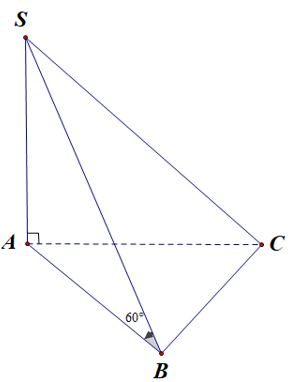
Ta có:
Câu 37:
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
Câu 38:
 Xem đáp án
Xem đáp án
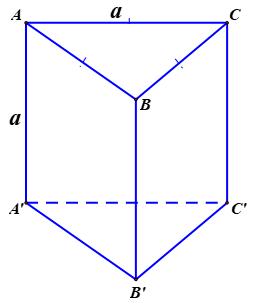
Vì đều cạnh a : .
Thể tích khối lăng trụ:
Câu 39:
 Xem đáp án
Xem đáp án
Chọn B
Vì một mặt là tam giác đều cạnh 2 nên:
Tổng diện tích tất cả các mặt của hình đa diện đó là:
Câu 40:
 Xem đáp án
Xem đáp án
Chọn C
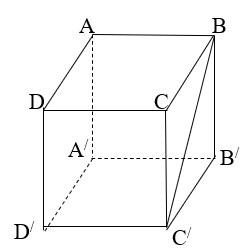
Giả sử khối lập phương có
Câu 41:
Cho khối tam giác có đường cao bằng 100cm và các cạnh đáy bằng 20cm, 21cm ,29cm . Tính thể tích của khối tam giác này.
 Xem đáp án
Xem đáp án
Chọn B
Giả sử khối tam giác
có
đường cao khối chóp
Ta có
.
Câu 42:
 Xem đáp án
Xem đáp án
Chọn D
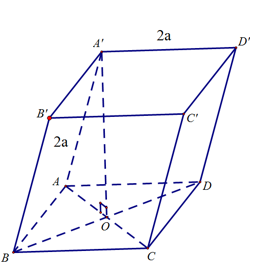
Gọi O là tâm hình vuông
Ta có:
Câu 44:
 Xem đáp án
Xem đáp án
Chọn C
Theo định nghĩa
Câu 46:
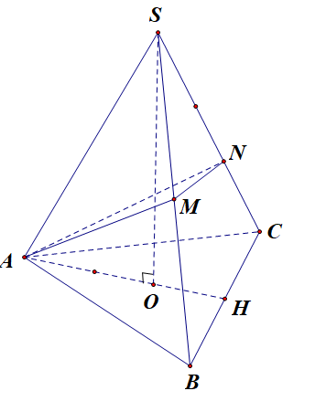
Cho hình chóp SABCDcó đáy ABCDlà hình thang vuông tại Góc giữa hai mặt phẳng ( SBC)và ( ABCD)là 60Gọi Ilà trung điểm của AD biết hai mặt phẳng ( SBI), ( CBI) cùng vuông góc với mặt phẳng ( ABCD)Tính thể tích khối chóp SABCD
 Xem đáp án
Xem đáp án
Chọn A
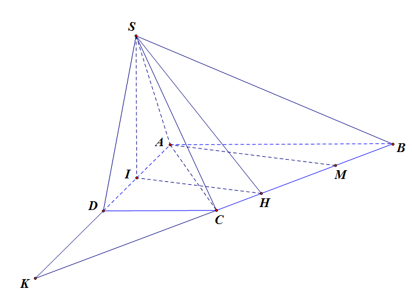
Ta có:
Kẻ ,
Suy ra: .
Kẻ
Trong là trung điểm AK
Ta có:
Áp dụng định lý Thales trong
Suy ra:
Câu 47:
 Xem đáp án
Xem đáp án
Chọn B
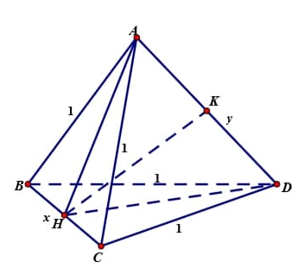
Đặt
Gọi lần lượt là trung điểm và
cân tại A và cân tại
Mặt khác, cân tại
Suy ra,
Ta có:
Áp dụng bất đắng thức Cauchy ta có:
Dấu xảy ra .
Do đó:
Khi đó:
Câu 48:
Cho hình chóp SABCD có đáy là hình thoi tâm O, , BD= 2a. Hai mặt phẳng (SAC) và ( SBD) cùng vuông góc với mặt đáy ( ABCD) . Biết khoảng cách từ tâm O đến ( SAB) bằng . Tính thể tích của khối chóp theo a.
 Xem đáp án
Xem đáp án
Chọn C
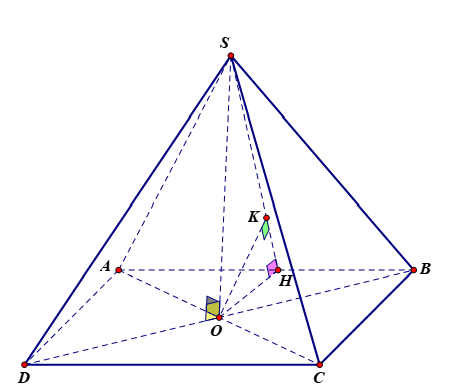
Vì nên .
Kẻ , .
Mà .
Do nên .
Xét vuông tại O, vì nên
.
Xét vuông tại O, vì nên
Diện tích mặt đáy ABCD là .
Thể tích hình chóp SABCD là .
Câu 49:
Cho hình lập phương cạnh a Gọi M, N lần lượt là trung điểm của A'B' và BC Mặt phẳng chia khối lập phương đã cho thành hai khối đa diện. Gọi là khối đa diện chứa đỉnh A, là khối đa diện còn lại. Tính tỉ số
 Xem đáp án
Xem đáp án
Chọn B
Đặt
Đường thẳng qua M song song với DN cắt A'D' tại K cắt B'C' tại I Thiết diện là hình ngũ giác
Dễ thấy
Ta có
Tương tự
Do đó
.
Suy ra
Câu 50:
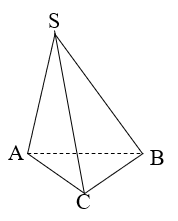
Cho hình chóp SABCD có đáy ABC là tam giác đều và có SA=SB=SC=1. Tính thể tích lớn nhất của khối chóp đã cho.
 Xem đáp án
Xem đáp án
Chọn A
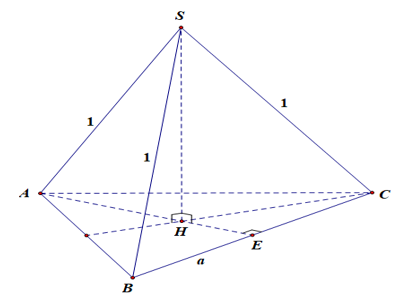
Gọi H là tâm của tam giác ABC đều. Gọi E là trung điểm của BC .
.
Đặt .
Xét tam giác : SAH .
Xét