Trắc nghiệm Toán lớp 10 Bài 16. Hàm số bậc hai có đáp án
-
606 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trục đối xứng của parabol y = x2 – 4x + 1
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trục đối xứng \[{\rm{x}}\,{\rm{ = }}\,--\frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{ = }}--\frac{{--\,{\rm{4}}}}{{\rm{2}}}{\rm{ = }}\,{\rm{2}}\].
Câu 2:
Tọa độ đỉnh I của hàm số y = – 3x2 + 4x – 1
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tọa độ đỉnh \[{\rm{I}}\left( {--\frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{;}}--\frac{{\rm{\Delta }}}{{{\rm{4a}}}}} \right)\]
Ta có giá trị \( - \frac{b}{{2a}} = - \frac{4}{{2.( - 3)}} = \frac{2}{3}\),
giá trị \( - \frac{\Delta }{{4a}} = - \frac{{{4^2} - 4.( - 3).( - 1)}}{{4.( - 3)}} = \frac{1}{3}\).
Vậy toạ độ đỉnh I\(\left( {\frac{2}{3};\frac{1}{3}} \right)\)
Câu 3:
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tọa độ đỉnh của hàm số là I(1; – 3)
Bảng biến thiên
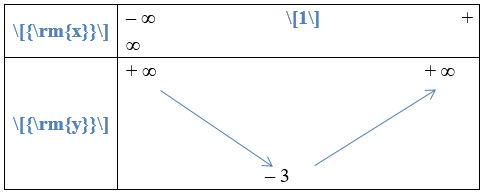
Từ bảng biến thiên ta có hàm số nghịch biến trên khoảng (– ∞; 1) nên cũng nghịch biến trên khoảng (– ∞; 0).
Câu 4:
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tọa độ đỉnh của parabol là \[{\rm{I}}\left( { - \frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{;}} - \frac{{\rm{\Delta }}}{{{\rm{4a}}}}} \right)\]
Ta có
\[\left\{ \begin{array}{l}--\frac{b}{{2a}} = - 1\\ - \frac{{{b^2} - 4ac}}{{4a}} = - 5\\a \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\4{a^2} - 8a = 0\\{\rm{a}} \ne {\rm{0}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\\left[ \begin{array}{l}a = 0\\a = 2\end{array} \right.\\{\rm{a}} \ne {\rm{0}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\end{array} \right.\]
Vậy a = 2 và b = 4.
Câu 5:
Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tọa độ đỉnh của hàm số là I(1; 2)
Bảng biến thiên
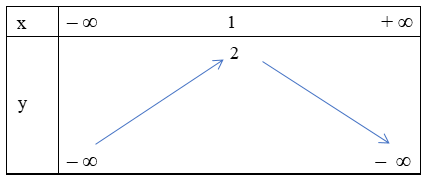
Từ bảng biến thiên ta có hàm số tăng từ trái sang phải trên khoảng (– ∞; 1) nên hàm số đồng biến trên khoảng (– ∞; 1).
Câu 6:
Cho parabol có đồ thị như hình sau:
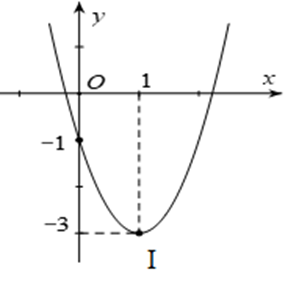
Tọa độ đỉnh I của parabol
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Từ đồ thị suy ra tọa độ đỉnh của hàm số là I(1; – 3).
Câu 7:
Cho hàm số y = f(x) có đồ thị như hình sau:
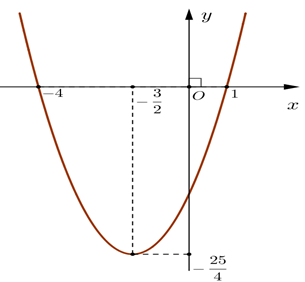
Hàm số đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đồ thị hàm số đi lên từ trái qua phải trên khoảng \[\left( {--\frac{{\rm{3}}}{{\rm{2}}}; + \infty } \right)\]nên hàm số đồng biến trên khoảng \[\left( {--\frac{3}{2}; + \infty } \right)\]
Câu 8:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
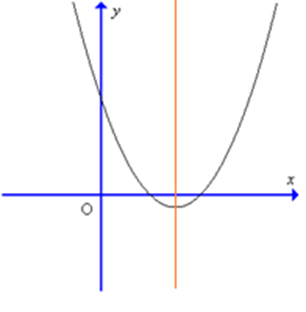
Kết luận nào sau đây đúng về hệ số a, b:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì bề lõm của đồ thị hướng lên trên nên a > 0;
Trục đối xứng của hàm số (đường màu đỏ) nằm bên phải trục Oy nên ta có trục đối xứng nhận giá trị dương hay \[{\rm{x}} = - \frac{{\rm{b}}}{{{\rm{2a}}}} > 0\] mà a > 0 nên b < 0.
Vậy a > 0 và b < 0.
Câu 9:
Hàm số y = x2 + 2x – 1 có bảng biến thiên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
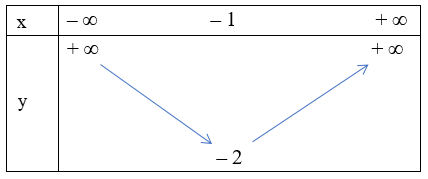
Tọa độ đỉnh của hàm số là I(– 1; – 2)
Vì hệ số a > 0 nên hàm số đồng biến trên khoảng (– 1; + ∞) và nghịch biến trên khoảng (– ∞; – 1) ta có bảng biến thiên
Câu 10:
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Giao điểm của đồ thị với trục tung tại A(0; – 1) nên đồ hàm số cắt trục tung tại điểm có tung độ âm. Do đó chỉ có hình C và hình D thỏa mãn.
Hàm số có trục đối xứng \[x = \frac{3}{8} > 0\]nên trục đối xứng nằm về phần dương của trục Ox.
Do đó hình D là hình vẽ đúng.
Câu 11:
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua A(0; 6) nên ta có hệ phương trình sau:
Vậy \[y = \frac{1}{2}{x^2} + 2x + 6\].
Câu 12:
Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đặt x + 2 = t ⇔ x = t – 2
Khi đó, ta có f(t) = (t – 2)2 – 3(t – 2) + 2 = t2 – 7t + 12
Vậy f(x) = x2 – 7x + 12.
Đáp án đúng là: D
Câu 13:
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?
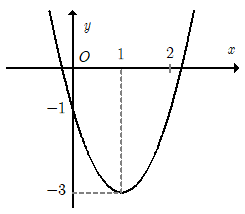
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Nhận xét:
Parabol có bề lõm hướng lên vậy a > 0. Loại đáp án C
Parabol giao trục tung tại A(0; – 1). Loại đáp án D
Parabol có trục đối xứng x = 1.
Xét đáp án A hàm số có trục đối xứng x = 2. Loại đáp án A
Đáp án B có trục đối xứng x = 1
Đáp án đúng là B
Câu 14:
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng \( - \frac{1}{4}\). Tính tích P = a.b.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì P đi qua điểm M(– 1; 6) và có tung độ đỉnh bằng \( - \frac{1}{4}\) nên ta có hệ
\( \Leftrightarrow \left\{ \begin{array}{l}a = 16\\b = 12\end{array} \right.\) (thỏa mãn a > 1) hoặc \(\left\{ \begin{array}{l}a = 1\\b = - 3\end{array} \right.\) (loại).
Suy ra P = a.b = 16.12 = 192.
Đáp án đúng là C.
Câu 15:
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì hàm số đạt cực đại tại x = 2 nên bề lõm của parabol quay xuống dưới, do đó a < 0.
Từ giả thiết ta có hệ \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\ - \frac{\Delta }{{4a}} = 3\\c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\{b^2} - 4ac = - 12a\\c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\16{a^2} + 16a = 0\\c = - 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\\c = - 1\end{array} \right.\)(loại) hoặc \(\left\{ \begin{array}{l}a = - 1\\b = 4\\c = - 1\end{array} \right.\) (thỏa mãn)
Vậy S = – 1 + 4 + (– 1) = 2.
