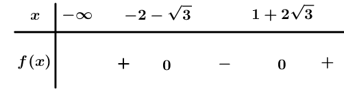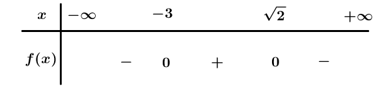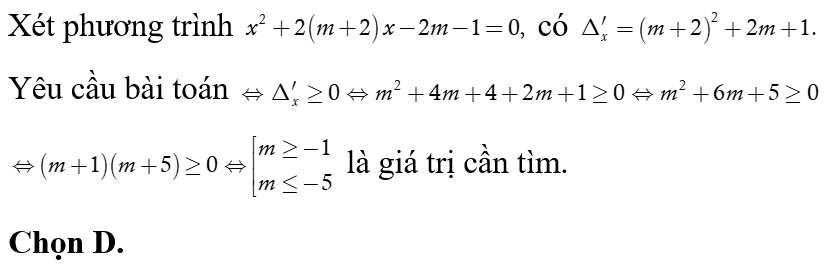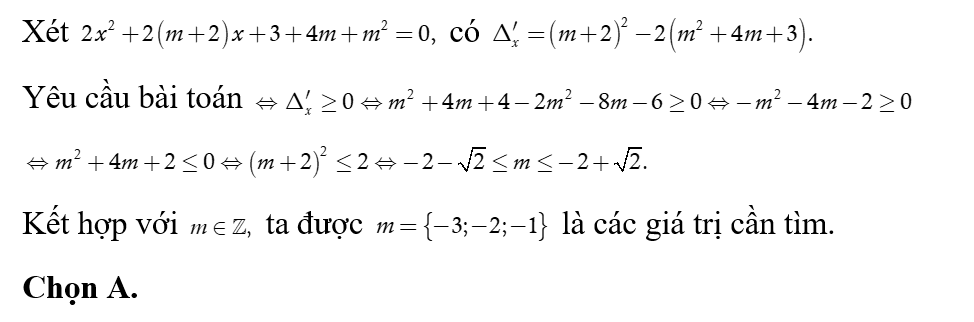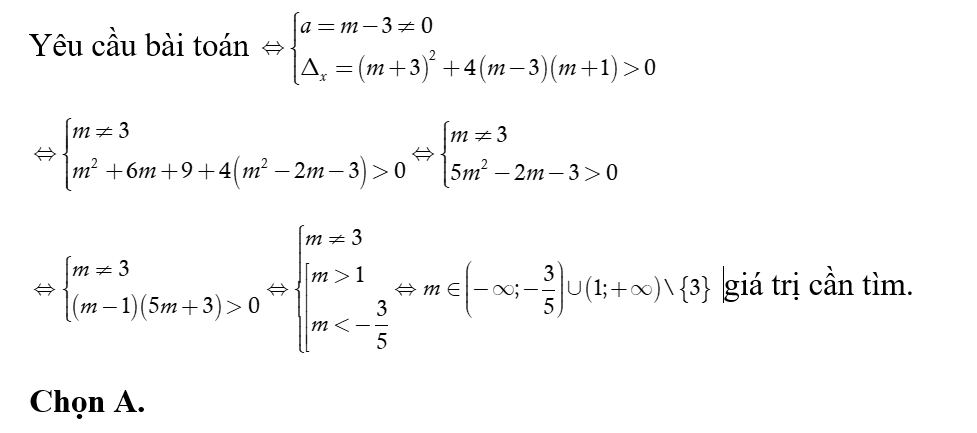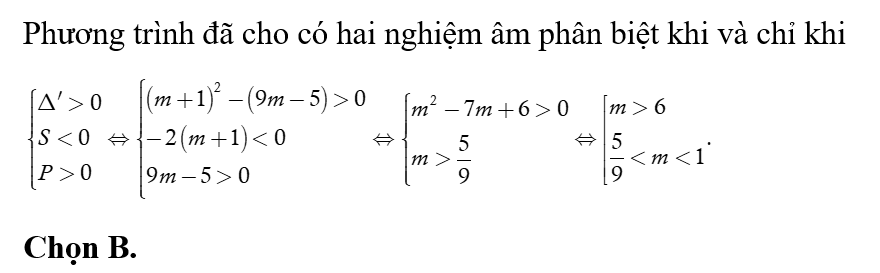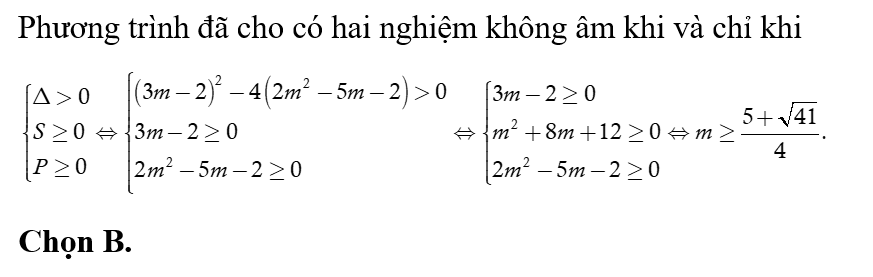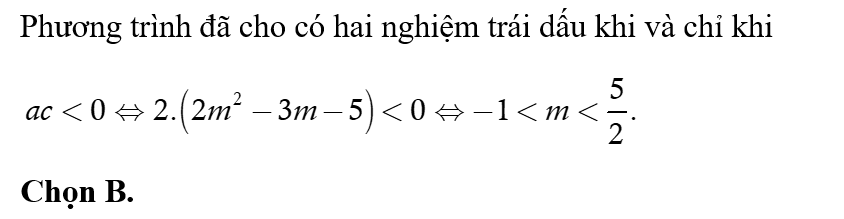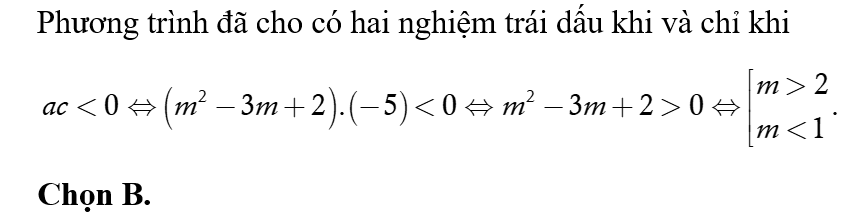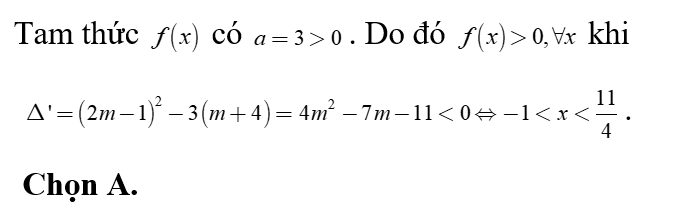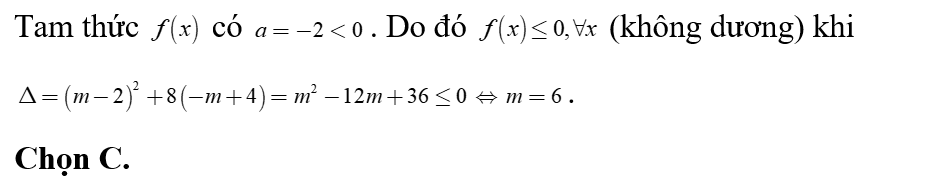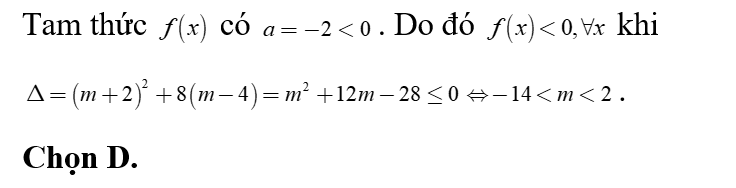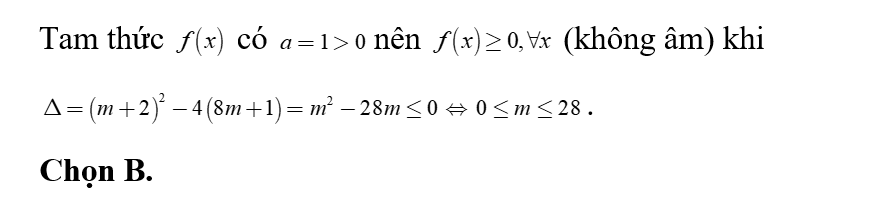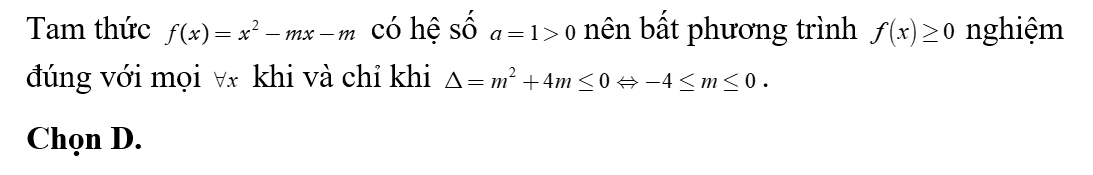75 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 5: Dấu của tam thức bậc hai có đáp án (Mới nhất)

Câu 1:

Cho $f (x) = a x^{2} + b x + c (a \neq 0) .$ Điều kiện để $f (x) > 0, \forall x \in ℝ$ là

A. $\{\begin{cases} a > 0 \\ Δ \leq 0 \end{cases} .$

B. $\{\begin{cases} a > 0 \\ Δ \geq 0 \end{cases} .$

C. $\{\begin{cases} a > 0 \\ Δ < 0 \end{cases} .$

D. $\{\begin{cases} a < 0 \\ Δ > 0 \end{cases} .$

f (x) > 0, \forall x \in ℝ

khi a > 0 và

Δ < 0

.

Chọn C.

Câu 2:

Cho

f (x) = a x^{2} + b x + c (a \neq 0)

. Điều kiện để

f (x) \geq 0, \forall x \in ℝ

là

A. $\{\begin{cases} a > 0 \\ Δ \leq 0 \end{cases}$

B. $\{\begin{cases} a > 0 \\ Δ \geq 0 \end{cases}$

C. $\{\begin{cases} a > 0 \\ Δ < 0 \end{cases}$

D. $\{\begin{cases} a < 0 \\ Δ > 0 \end{cases}$

Xem đáp án

f (x) < 0, \forall x \in ℝ

khi a< 0 và

Δ < 0

. Chọn A.

Câu 3:

Cho

f (x) = a x^{2} + b x + c (a \neq 0)

. Điều kiện để

f (x) < 0, \forall x \in ℝ

là

A. $\{\begin{cases} a < 0 \\ Δ \leq 0 \end{cases}$

B. $\{\begin{cases} a < 0 \\ Δ = 0 \end{cases}$

C. $\{\begin{cases} a > 0 \\ Δ < 0 \end{cases}$

D. $\{\begin{cases} a < 0 \\ Δ < 0 \end{cases}$

Xem đáp án

f (x) < 0, \forall x \in ℝ

khi

a < 0

và

Δ < 0

. Chọn D.

Câu 4:

Cho

f (x) = a x^{2} + b x + c (a \neq 0)

. Điều kiện để

f (x) \leq 0, \forall x \in ℝ

là

A. $\{\begin{cases} a < 0 \\ Δ \leq 0 \end{cases}$

B. $\{\begin{cases} a < 0 \\ Δ \geq 0 \end{cases}$

C. $\{\begin{cases} a > 0 \\ Δ < 0 \end{cases}$

D. $\{\begin{cases} a < 0 \\ Δ > 0 \end{cases}$

Xem đáp án

f (x) \leq 0, \forall x \in ℝ

khi a < 0 và

Δ \leq 0

. Chọn A.

Câu 5:

Cho $f (x) = a x^{2} + b x + c (a \neq 0)$ có $Δ = b^{2} - 4 a c < 0$ . Khi đó mệnh đề R nào đúng?

A.

f (x) > 0, \forall x \in ℝ

.

B. $f (x) < 0, \forall x \in ℝ$ .

C.

f (x)

không đổi dấu.

D. Tồn tại x để

f (x) = 0

.

Xem đáp án

Vì $Δ < 0$ và $a \neq 0$ nên f(x) không đổi dấu trên R. Chọn C.

Câu 6:

Tam thức bậc hai $f (x) = - x^{2} + 5 x - 6$ nhận giá trị dương khi và chỉ khi

A. $x \in (- \infty; 2) .$

B. $(3; + \infty) .$

C. $x \in (2; + \infty) .$

D. $x \in (2; 3) .$

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 3 \end{array}$ .

Bảng xét dấu

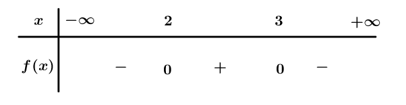
Dựa vào bảng xét dấu $f (x) > 0 \Leftrightarrow x \in (2; 3) .$

Chọn D.

Câu 7:

Tam thức bậc hai $f (x) = 2 x^{2} + 2 x + 5$ nhận giá trị dương khi và chỉ khi

A. $x \in (0; + \infty) .$

B. $x \in (- 2; + \infty) .$

C. $x \in ℝ$

D. $x \in (- \infty; 2) .$

Xem đáp án

Ta có $\{\begin{cases} a = 2 > 0 \\ Δ' = 1 - 2.5 = - 9 < 0 \end{cases} \Rightarrow f (x) > 0, \forall x \in ℝ .$ Chọn C.

Câu 8:

Tam thức bậc hai $f (x) = x^{2} + (\sqrt{5} - 1) x - \sqrt{5}$ nhận giá trị dương khi và chỉ khi

A. $x \in (- \sqrt{5}; 1) .$

B. $x \in (- \sqrt{5}; + \infty) .$

C. $x \in (- \infty; - \sqrt{5}) \cup (1; + \infty) .$

D. $x \in (- \infty; 1) .$

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - \sqrt{5} \end{array}$ .

Bảng xét dấu:

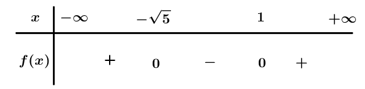
Dựa vào bảng xét dấu $f (x) > 0 \Leftrightarrow x \in (- \infty; - \sqrt{5}) \cup (1; + \infty) .$ Chọn C.

Tam thức bậc hai

f (x) = x^{2} + (\sqrt{5} - 1) x - \sqrt{5}

nhận giá trị dương khi và chỉ khi

Câu 9:

Tam thức bậc hai $f (x) = - x^{2} + 3 x - 2$ nhận giá trị không âm khi và chỉ khi

A. $x \in (- \infty; 1) \cup (2; + \infty)$

B. $x \in [1; 2]$

C. $x \in (- \infty; 1] \cup [2; + \infty)$

D. $x \in (1; 2)$

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 2 \end{array}$ .

Bảng xét dấu

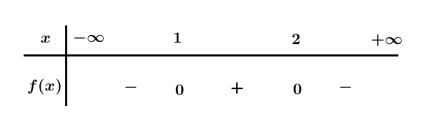
Dựa vào bảng xét dấu $f (x) \geq 0 \Leftrightarrow 1 \leq x \leq 2$ . Chọn B.

Câu 10:

Số giá trị nguyên của x để tam thức $f (x) = 2 x^{2} - 7 x - 9$ nhận giá trị âm là

A. 3

B. 4

C. 5

D. 6

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = \frac{9}{2} \end{array}$ . Bảng xét dấu

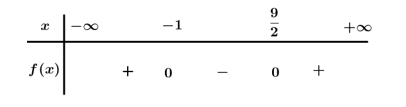
Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow - 1 < x < \frac{9}{2} .$ Mà x nguyên nên $x \in \{0; 1; 2; 3; 4\}$ .

Chọn A.

Câu 11:

Tam thức bậc hai $f (x) = x^{2} + (1 - \sqrt{3}) x - 8 - 5 \sqrt{3}$ :

A. Dương với mọi

x \in ℝ

.

B. Âm với mọi $x \in ℝ$ .

C. Âm với mọi

x \in (- 2 - \sqrt{3}; 1 + 2 \sqrt{3})

.

D. Âm với mọi

x \in (- \infty; 1)

.

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = - 2 - \sqrt{3} \\ x = 1 + 2 \sqrt{3} \end{array}$ .

Bảng xét dấu

Tam thức bậc hai f(x) = x^2+ ( 1- căn bậc hai 3)x-8-5 căn bậc hai 3 : (ảnh 1)

Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow - 2 - \sqrt{3} < x < 1 + 2 \sqrt{3}$ .

Chọn C.

Câu 12:

Tam thức bậc hai $f (x) = (1 - \sqrt{2}) x^{2} + (5 - 4 \sqrt{2}) x - 3 \sqrt{2} + 6$

A. Dương với mọi $x \in ℝ$ .

B. Dương với mọi $x \in (- 3; \sqrt{2})$ .

C. Dương với mọi

x \in (- 4; \sqrt{2})

.

D. Âm với mọi

x \in ℝ

.

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = \sqrt{2} \end{array}$ .

Bảng xét dấu

Tam thức bậc hai f(x) = ( 1- căn bậc hai 2)x^2+ (5- 4 căn bậc hai 2)x- 3 căn bậc hai 2+ 6 (ảnh 1)

Dựa vào bảng xét dấu $f (x) > 0 \Leftrightarrow - 3 < x < \sqrt{2}$ .

Chọn B.

Câu 13:

Cho $f (x) = x^{2} - 4 x + 3$ . Trong các mệnh đề sau, mệnh đề đúng là:

A. $f (x) < 0, \forall x \in (- \infty; 1] \cup [3; + \infty)$

B. $f (x) \leq 0, \forall x \in [1; 3]$

C. $f (x) \geq 0, \forall x \in (- \infty; 1) \cup (3; + \infty)$

D. $f (x) > 0, \forall x \in [1; 3]$

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = 1 \end{array}$ .

Bảng xét dấu

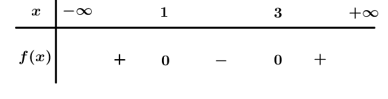
Cho f(x)= x^2-4x+3 . Trong các mệnh đề sau, mệnh đề đúng là: (ảnh 1)

Dựa vào bảng xét dấu $f (x) \leq 0 \Leftrightarrow 1 \leq x \leq 3$ .

Chọn B.

Câu 14:

Dấu của tam thức bậc 2: $f (x) = - x^{2} + 5 x - 6$ được xác định như sau:

A. $f (x) < 0$ với $2 < x < 3$ và $f (x) > 0$ với $x < 2$ hoặc $x > 3$ .

B. $f (x) < 0$ với $- 3 < x < - 2$ và $f (x) > 0$ với $x < - 3$ hoặc $x > - 2$ .

C. $f (x) > 0$ với $2 < x < 3$ và $f (x) < 0$ với $x < 2$ hoặc $x > 3$ .

D.

f (x) > 0

với

- 3 < x < - 2

và

f (x) < 0

với

x < - 3

hoặc

x > - 2

.

Xem đáp án

Ta có $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = 2 \end{array}$ .

Bảng xét dấu

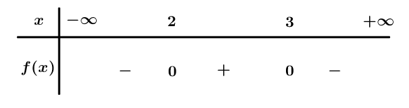
Dấu của tam thức bậc 2: f(x)= -x^2+5x-6 được xác định như sau: (ảnh 1)

Dựa vào bảng xét dấu ta được

$f (x) > 0$ với $2 < x < 3$ và $f (x) < 0$ với x < 2 hoặc x > 3.

Chọn C.

Câu 15:

Cho các tam thức $f (x) = 2 x^{2} - 3 x + 4; g (x) = - x^{2} + 3 x - 4; h (x) = 4 - 3 x^{2}$ . Số tam thức đổi dấu trên $ℝ$ là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Vì $f (x) = 0$ vô nghiệm, $g (x) = 0$ vô nghiệm, $h (x) = 0$ có hai nghiệm phân biệt nên chỉ có $h (x)$ đổi dấu trên $ℝ$ .

Chọn B.

Câu 16:

Tập nghiệm của bất phương trình: $2 x^{2} - 7 x - 15 \geq 0$ là:

A. $(- \infty; - \frac{3}{2}] \cup [5; + \infty)$

B. $[- \frac{3}{2}; 5]$

C. $(- \infty; - 5] \cup [\frac{3}{2}; + \infty)$

D. $[- 5; \frac{3}{2}]$

Xem đáp án

Ta có $2 x^{2} - 7 x - 15 = 0 \Leftrightarrow [\begin{array}{l} x = 5 \\ x = - \frac{3}{2} \end{array}$ .

Bảng xét dấu

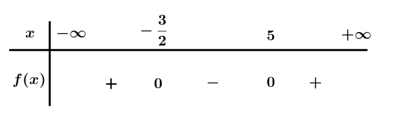
Tập nghiệm của bất phương trình: 2x^2-7x-15 lớn hơn bằng 0 là: (ảnh 1)

Dựa vào bảng xét dấu $2 x^{2} - 7 x - 15 \geq 0 \Leftrightarrow [\begin{array}{l} x \geq 5 \\ x \leq - \frac{3}{2} \end{array} .$

Chọn A.

Câu 17:

Tập nghiệm của bất phương trình: $- x^{2} + 6 x + 7 \geq 0$ là:

A. $(- \infty; - 1] \cup [7; + \infty)$

B. $[- 1; 7]$

C. $(- \infty; - 7] \cup [1; + \infty)$

D. $[- 7; 1]$

Xem đáp án

Ta có $- x^{2} + 6 x + 7 = 0 \Leftrightarrow [\begin{array}{l} x = 7 \\ x = - 1 \end{array}$ .

Bảng xét dấu

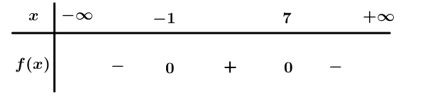
Tập nghiệm của bất phương trình: -x^2+6x+7 lớn hơn bằng 0 là: (ảnh 1)

Dựa vào bảng xét dấu $- x^{2} + 6 x + 7 \geq 0 \Leftrightarrow - 1 \leq x \leq 7.$

Chọn B.

Câu 18:

Giải bất phương trình $- 2 x^{2} + 3 x - 7 \geq 0.$

A. $S = 0.$

B. $S = \{0\} .$

C. $S = \emptyset .$

D. $S = ℝ .$

Xem đáp án

Ta có $- 2 x^{2} + 3 x - 7 = 0$ vô nghiệm.

Bảng xét dấu

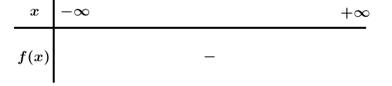
Giải bất phương trình -2x^2+3x-7 lớn hơn bằng 0 (ảnh 1)

Dựa vào bảng xét dấu $- 2 x^{2} + 3 x - 7 \geq 0 \Leftrightarrow x \in \emptyset$ .

Chọn C.

Câu 19:

Tập nghiệm của bất phương trình $x^{2} - 3 x + 2 < 0$ là:

A. $(- \infty; 1) \cup (2; + \infty) .$

B. $(2; + \infty) .$

C. $(1; 2) .$

D. $(- \infty; 1) .$

Xem đáp án

Ta có $f (x) = x^{2} - 3 x + 2 = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 1 \end{array}$ .

Bảng xét dấu

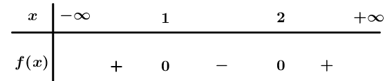
Tập nghiệm của bất phương trình x^2 - 3x+2 < 0 là: (ảnh 1)

Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow 1 < x < 2$ .

Chọn C.

Câu 20:

Tập nghiệm của bất phương trình

- x^{2} + 5 x - 4 < 0

là

A. $[1; 4]$

B. $(1; 4)$

C. $(- \infty; 1) \cup (4; + \infty)$

D. $(- \infty; 1] \cup [4; + \infty)$

Xem đáp án

Ta có $f (x) = - x^{2} + 5 x - 4 = 0 \Leftrightarrow [\begin{array}{l} x = 4 \\ x = 1 \end{array}$ .

Bảng xét dấu

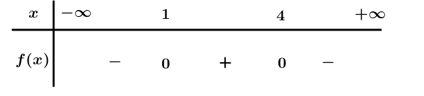
Tập nghiệm của bất phương trình -x^2+5x-4 < 0 là (ảnh 1)

Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow [\begin{array}{l} x < 1 \\ x > 4 \end{array}$ .

Chọn C.

Câu 21:

Tập nghiệm của bất phương trình $\sqrt{2} x^{2} - (\sqrt{2} + 1) x + 1 < 0$ là:

A. $(\frac{\sqrt{2}}{2}; 1) .$

B. $\emptyset .$

C. $[\frac{\sqrt{2}}{2}; 1] .$

D. $(- \infty; \frac{\sqrt{2}}{2}) \cup (1; + \infty) .$

Xem đáp án

Ta có $f (x) = \sqrt{2} x^{2} - (\sqrt{2} + 1) x + 1 = 0 \Leftrightarrow [\begin{array}{l} x = \frac{\sqrt{2}}{2} \\ x = 1 \end{array}$ .

Bảng xét dấu

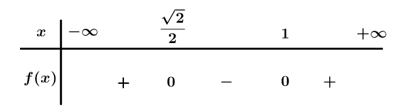
Tập nghiệm của bất phương trình căn bậc hai 2x^2- ( căn bậc hai 2+1)x+1 <0 là: (ảnh 1)

Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow \frac{\sqrt{2}}{2} < x < 1$ .

Chọn A.

Câu 22:

Tập nghiệm của bất phương trình $6 x^{2} + x - 1 \leq 0$ là

A. $[- \frac{1}{2}; \frac{1}{3}]$

B. $(- \frac{1}{2}; \frac{1}{3})$

C. $(- \infty; - \frac{1}{2}) \cup (\frac{1}{3}; + \infty)$

D. $(- \infty; - \frac{1}{2}] \cup [\frac{1}{3}; + \infty)$

Xem đáp án

Ta có $f (x) = 6 x^{2} + x - 1 = 0 \Leftrightarrow [\begin{array}{l} x = \frac{1}{3} \\ x = - \frac{1}{2} \end{array}$ .

Bảng xét dấu

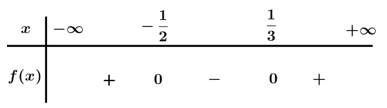
Tập nghiệm của bất phương trình 6x^2+x-1 bé hơn bằng 0là (ảnh 1)

Dựa vào bảng xét dấu $f (x) \leq 0 \Leftrightarrow - \frac{1}{2} \leq x \leq \frac{1}{3}$ .

Chọn A.

Câu 23:

Số thực dương lớn nhất thỏa mãn $x^{2} - x - 12 \leq 0$ là ?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Ta có $f (x) = x^{2} - x - 12 = 0 \Leftrightarrow [\begin{array}{l} x = 4 \\ x = - 3 \end{array}$ .

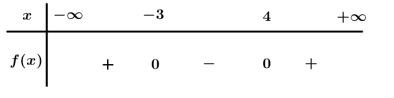
Bảng xét dấu

Số thực dương lớn nhất thỏa mãn x^2-x-12 bé hơn bằng 0 là ? (ảnh 1)

Dựa vào bảng xét dấu $f (x) \leq 0 \Leftrightarrow - 3 \leq x \leq 4$ . Suy ra số thực dương lớn nhất thỏa $x^{2} - x - 12 \leq 0$ là 4.

Chọn D.

Câu 24:

Bất phương trình nào sau đây có tập nghiệm $ℝ$ là ?

A. $- 3 x^{2} + x - 1 \geq 0.$

B. $- 3 x^{2} + x - 1 > 0.$

C. $- 3 x^{2} + x - 1 < 0.$

D. $3 x^{2} + x - 1 \leq 0.$

Xem đáp án

Xét $f (x) = - 3 x^{2} + x - 1$ có $a = - 3 < 0, Δ = 1^{2} - 4. (- 3) . (- 1) = - 11 < 0$ nên $f (x) < 0, \forall x$ tức là tập nghiệm của bất phương trình là $ℝ$ . Chọn C

Câu 25:

Cho bất phương trình $x^{2} - 8 x + 7 \geq 0$ . Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất

phương trình.

A. $(- \infty; 0] .$

B. $[8; + \infty) .$

C. $(- \infty; 1] .$

D. $[6; + \infty) .$

Xem đáp án

Ta có $f (x) = x^{2} - 8 x + 7 = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 7 \end{array}$ .

Bảng xét dấu

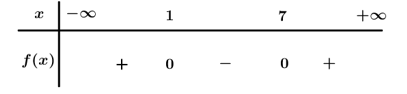
Cho bất phương trình x^2-8x+7 lớn hơn bằng 0. Trong các tập hợp sau đây, tập nào có chứ (ảnh 1)

Dựa vào bảng xét dấu $f (x) \geq 0 \Leftrightarrow [\begin{array}{l} x \leq 1 \\ x \geq 7 \end{array}$ .

Tập nghiệm của bất phương trình là $S = (- \infty; 1] \cup [7; + \infty)$ .

Vì $\frac{13}{2} \in [6; + \infty)$ và $\frac{13}{2} \notin S$ nên $[6; + \infty)$ thỏa yêu cầu bài toán. Chọn D.

Câu 26:

Giải bất phương trình

x (x + 5) \leq 2 (x^{2} + 2) .

A. $x \leq 1 .$

B. $1 \leq x \leq 4.$

C. $x \in (- \infty; 1] \cup [4; + \infty) .$

D. $x \geq 4.$

Xem đáp án

Bất phương trình $x (x + 5) \leq 2 (x^{2} + 2) \Leftrightarrow x^{2} + 5 x \leq 2 x^{2} + 4 \Leftrightarrow x^{2} - 5 x + 4 \geq 0$

Xét phương trình $x^{2} - 5 x + 4 = 0 \Leftrightarrow (x - 1) (x - 4) = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 4 \end{array} .$

Lập bảng xét dấu

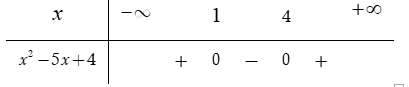
Giải bất phương trình x(x+5) bé hơn bằng 2( x^2+2) (ảnh 1)

Dựa vào bảng xét dấu, ta thấy $x^{2} - 5 x + 4 \geq 0 \Leftrightarrow x \in (- \infty; 1] \cup [4; + \infty) .$

Chọn C.

Câu 27:

Biểu thức $(3 x^{2} - 10 x + 3) (4 x - 5)$ âm khi và chỉ khi

A. $x \in (- \infty; \frac{5}{4}) .$

B. $x \in (- \infty; \frac{1}{3}) \cup (\frac{5}{4}; 3) .$

C. $x \in (\frac{1}{3}; \frac{5}{4}) \cup (3; + \infty) .$

D. $x \in (\frac{1}{3}; 3) .$

Xem đáp án

Đặt $f (x) = (3 x^{2} - 10 x + 3) (4 x - 5)$

Phương trình $3 x^{2} - 10 x + 3 = 0 \Leftrightarrow [\begin{matrix} x = 3 \\ x = \frac{1}{3} \end{matrix}$ và $4 x - 5 = 0 \Leftrightarrow x = \frac{5}{4} .$

Lập bảng xét dấu

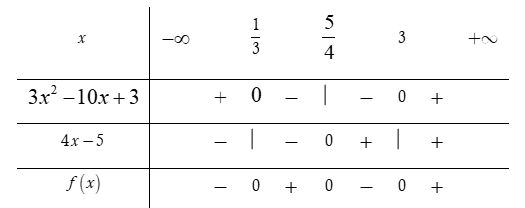
Biểu thức (3x^2-10x+3)(4x-5) âm khi và chỉ khi (ảnh 1)

Dựa vào bảng xét dấu, ta thấy $f (x) < 0 \Leftrightarrow x \in (- \infty; \frac{1}{3}) \cup (\frac{5}{4}; 3) .$

Chọn B.

Câu 28:

Cặp bất phương trình nào sau đây là tương đương?

A. $x - 2 \leq 0$ và $x^{2} (x - 2) \leq 0.$

B. $x - 2 < 0$ và $x^{2} (x - 2) > 0.$

C.

x - 2 < 0

và

x^{2} (x - 2) < 0.

D.

x - 2 \geq 0

và

x^{2} (x - 2) \geq 0.

Xem đáp án

Đặt $f (x) = x^{2} (x - 2) .$

Phương trình $x^{2} = 0 \Leftrightarrow x = 0$ và $x - 2 = 0 \Leftrightarrow x = 2.$

Lập bảng xét dấu

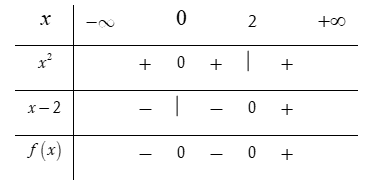
Cặp bất phương trình nào sau đây là tương đương? (ảnh 1)

Dựa vào bảng xét dấu ta thấy rằng bất phương trình $x - 2 \geq 0 \Leftrightarrow x^{2} (x - 2) \geq 0.$

Chọn D.

Câu 29:

Biểu thức $(4 - x^{2}) (x^{2} + 2 x - 3) (x^{2} + 5 x + 9)$ âm khi

A. $x \in (1; 2)$

B. $x \in (- 3; - 2) \cup (1; 2)$

C. $x \geq 4.$

D. $x \in (- \infty; - 3) \cup (- 2; 1) \cup (2; + \infty)$

Xem đáp án

Đặt $f (x) = (4 - x^{2}) (x^{2} + 2 x - 3) (x^{2} + 5 x + 9)$

Phương trình $4 - x^{2} = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x = - 2 \end{array} .$

Phương trình $x^{2} + 2 x - 3 = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 3 \end{array} .$

Ta có $x^{2} + 5 x + 9 = {(x + \frac{5}{2})}^{2} + \frac{11}{4} > 0 \Rightarrow x^{2} + 5 x + 9 = 0 \Leftrightarrow x \in \emptyset .$ Lập bảng xét dấu:

Biểu thức (4-x^2)( x^2+2x-3)(x^2+5x+9) âm khi (ảnh 1)

Dựa vào bảng xét dấu ta thấy $(4 - x^{2}) (x^{2} + 2 x - 3) (x^{2} + 5 x + 9) < 0 \Leftrightarrow [\begin{array}{l} x < - 3 \\ - 2 < x < 1 \\ x > 2 \end{array}$

$\Leftrightarrow x \in (- \infty; - 3) \cup (- 2; 1) \cup (2; + \infty) .$

Chọn D.

Câu 30:

Tập nghiệm của bất phương trình $x^{3} + 3 x^{2} - 6 x - 8 \geq 0$ là

A. $x \in [- 4; - 1] \cup [2; + \infty) .$

B. $x \in (- 4; - 1) \cup (2; + \infty) .$

C. $x \in [- 1; + \infty) .$

D. $x \in (- \infty; - 4] \cup [- 1; 2] .$

Xem đáp án

Bất phương trình $x^{3} + 3 x^{2} - 6 x - 8 \geq 0 \Leftrightarrow (x - 2) (x^{2} + 5 x + 4) \geq 0.$

Phương trình $x^{2} + 5 x + 4 = 0 \Leftrightarrow [\begin{matrix} x = - 4 \\ x = - 1 \end{matrix}$ và $x - 2 = 0 \Leftrightarrow x = 2.$

Lập bảng xét dấu

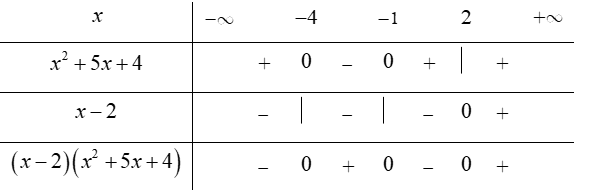
Tập nghiệm của bất phương trình x^3+ 3x^2-6x-8 lớn hơn bằng 0 là (ảnh 1)

Dựa vào bảng xét dấu, ta thấy rằng $(x - 2) (x^{2} + 5 x + 4) \geq 0 \Leftrightarrow x \in [- 4; - 1] \cup [2; + \infty) .$

Chọn A.

Câu 31:

Biểu thức $f (x) = \frac{11 x + 3}{- x^{2} + 5 x - 7}$ nhận giá trị dương khi và chỉ khi

A. $x \in (- \frac{3}{11}; + \infty) .$

B. $x \in (- \frac{3}{11}; 5) .$

C. $x \in (- \infty; - \frac{3}{11}) .$

D. $x \in (- 5; - \frac{3}{11}) .$

Xem đáp án

Ta có $- x^{2} + 5 x - 7 = - (x^{2} - 5 x + 7) = - {(x - \frac{5}{2})}^{2} - \frac{3}{4} < 0, \forall x \in ℝ .$

Do đó, bất phương trình $f (x) > 0 \Leftrightarrow 11 x + 3 < 0 \Leftrightarrow x < - \frac{3}{11} \Leftrightarrow x \in (- \infty; - \frac{3}{11}) .$

Chọn C.

Câu 32:

Tập nghiệm S của bất phương trình $\frac{x - 7}{4 x^{2} - 19 x + 12} > 0$ là

A. $S = (- \infty; \frac{3}{4}) \cup (4; 7) .$

B. $S = (\frac{3}{4}; 4) \cup (7; + \infty) .$

C. $S = (\frac{3}{4}; 4) \cup (4; + \infty) .$

D. $S = (\frac{3}{4}; 7) \cup (7; + \infty) .$

Xem đáp án

Điều kiện:

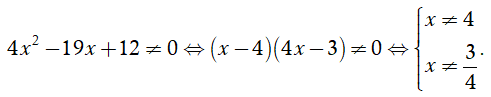
Tập nghiệm S của bất phương trình x-7/ 4x^2- 19x+12 là (ảnh 1)

Phương trình $x - 7 = 0 \Leftrightarrow x = 7$ và $4 x^{2} - 19 x + 12 = 0 \Leftrightarrow [\begin{array}{l} x = 4 \\ x = \frac{3}{4} \end{array} .$

Bảng xét dấu:

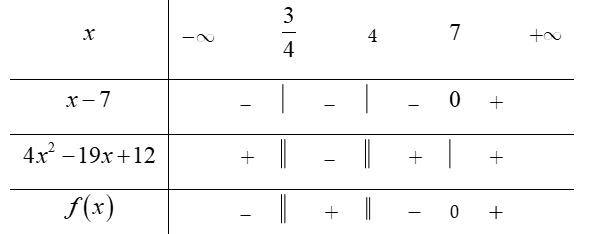
Tập nghiệm S của bất phương trình x-7/ 4x^2- 19x+12 là (ảnh 2)

Dựa vào bảng xét dấu, bất phương trình $\frac{x - 7}{4 x^{2} - 19 x + 12} > 0 \Leftrightarrow [\begin{array}{l} \frac{3}{4} < x < 4 \\ x > 7 \end{array} .$

Vậy tập nghiệm của bất phương trình là $S = (\frac{3}{4}; 4) \cup (7; + \infty) .$ Chọn B.

Câu 33:

Có bao nhiêu giá trị nguyên dương của x thỏa mãn $\frac{x + 3}{x^{2} - 4} - \frac{1}{x + 2} < \frac{2 x}{2 x - x^{2}}$ ?

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Điều kiện: $\{\begin{cases} x^{2} - 4 \neq 0 \\ x + 2 \neq 0 \\ 2 x - x^{2} \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq 0 \\ x \neq \pm 2 \end{cases} .$ Bất phương trình:

$\frac{x + 3}{x^{2} - 4} - \frac{1}{x + 2} < \frac{2 x}{2 x - x^{2}} \Leftrightarrow \frac{x + 3}{x^{2} - 4} - \frac{1}{x + 2} + \frac{2 x}{x^{2} - 2 x} < 0 \Leftrightarrow \frac{2 x + 9}{x^{2} - 4} < 0.$

Bảng xét dấu:

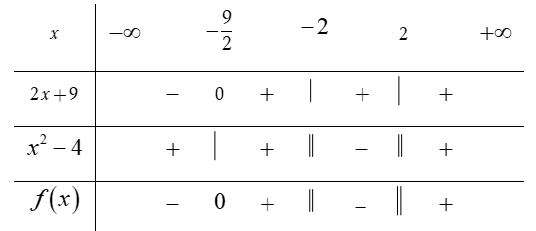
Có bao nhiêu giá trị nguyên dương của x thỏa mãn x+3/x^2-4/ 1/x+2< 2x/ 2x-x^2? (ảnh 1)

Dựa vào bảng xét dấu, ta thấy $\frac{2 x + 9}{x^{2} - 4} < 0 \Leftrightarrow x \in (- \infty; - \frac{9}{2}) \cup (- 2; 2) .$

Vậy có chỉ có duy nhất một giá trị nguyên dương của $x (x = 1)$ thỏa mãn yêu cầu.

Chọn C.

Câu 34:

Tập nghiệm của bất phương trình $\frac{- 2 x^{2} + 7 x + 7}{x^{2} - 3 x - 10} \leq - 1$ là

A. Hai khoảng.

B. Một khoảng và một đoạn.

C. Hai khoảng và một đoạn.

D. Ba khoảng.

Xem đáp án

Điều kiện: $x^{2} - 3 x - 10 \neq 0 \Leftrightarrow (x + 2) (x - 5) \neq 0 \Leftrightarrow \{\begin{cases} x \neq - 2 \\ x \neq 5 \end{cases} .$

Bất phương trình

$\frac{- 2 x^{2} + 7 x + 7}{x^{2} - 3 x - 10} \leq - 1 \Leftrightarrow \frac{- 2 x^{2} + 7 x + 7}{x^{2} - 3 x - 10} + 1 \leq 0 \Leftrightarrow \frac{- x^{2} + 4 x - 3}{x^{2} - 3 x - 10} \leq 0 (*) .$

Bảng xét dấu

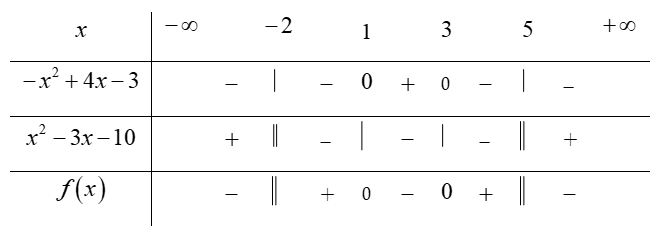
Tập nghiệm của bất phương trình -2x^2+7x+7/ x^2-3x-10 bé hơn bằng -1 là (ảnh 1)

Dựa vào bảng xét dấu, bất phương trình $(*) \Leftrightarrow x \in (- \infty; - 2) \cup [1; 3] \cup (5; + \infty) .$

Chọn C.

Câu 35:

Hỏi có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình $\frac{x^{4} - x^{2}}{x^{2} + 5 x + 6} \leq 0$ ?

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Bất phương trình $\frac{x^{4} - x^{2}}{x^{2} + 5 x + 6} \leq 0 \Leftrightarrow \frac{x^{2} (x^{2} - 1)}{x^{2} + 5 x + 6} \leq 0 (*) .$

Vì $x^{2} \geq 0, \forall x \in ℝ$ nên bất phương trình

$(*) \Leftrightarrow [\begin{array}{l} x^{2} = 0 \\ \frac{x^{2} - 1}{x^{2} + 5 x + 6} \leq 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ f (x) = \frac{x^{2} - 1}{x^{2} + 5 x + 6} \leq 0 \end{array} .$

Phương trình $x^{2} - 1 = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 1 \end{array}$ và $x^{2} + 5 x + 6 = 0 \Leftrightarrow [\begin{array}{l} x = - 2 \\ x = - 3 \end{array} .$

Bảng xét dấu

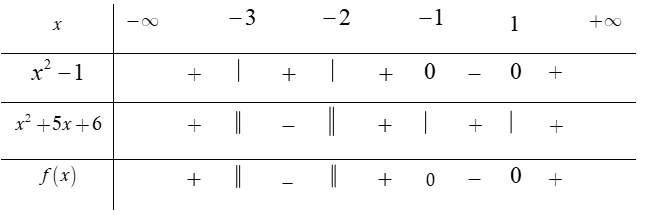
Hỏi có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình x^4-x^2/ x^2+5x+6 bé hơn bằng 0 ? (ảnh 1)

Dựa vào bảng xét dấu, ta thấy

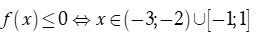
Kết hợp với $x \in Z$ ta được $x = \{- 1; 0; 1\}$

Vậy có tất cả 3 giá trị nguyên cần tìm.

Chọn D.

Câu 36:

Tìm tập xác định D của hàm số

y = \sqrt{2 x^{2} - 5 x + 2} .

A. $D = (- \infty; \frac{1}{2}] .$

B. $D = [2; + \infty) .$

C. $D = (- \infty; \frac{1}{2}] \cup [2; + \infty) .$

D. $D = [\frac{1}{2}; 2] .$

Xem đáp án

Hàm số đã cho xác định khi và chỉ khi

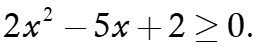
Tìm tập xác định D của hàm số y= căn bậc hai 2x^2-5x+2 (ảnh 1)

Phương trình

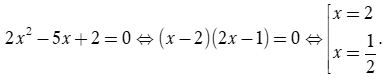
Bảng xét dấu:

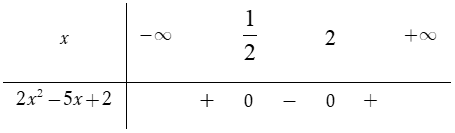
Tìm tập xác định D của hàm số y= căn bậc hai 2x^2-5x+2 (ảnh 3)

Dựa vào bảng xét dấu, ta thấy

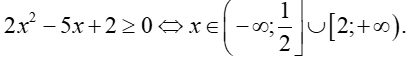
Tìm tập xác định D của hàm số y= căn bậc hai 2x^2-5x+2 (ảnh 4)

Vậy tập xác định của hàm số là

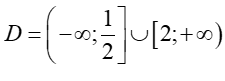
Chọn C.

Câu 37:

Giá trị nguyên dương lớn nhất để hàm số $y = \sqrt{5 - 4 x - x^{2}}$ xác định là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Hàm số đã cho xác định khi và chỉ khi

Phương trình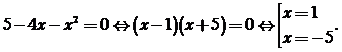

Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy

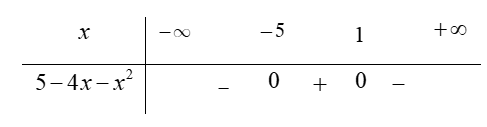
Vậy nghiệm dương lớn nhất để hàm số xác định là x = 1.

Chọn A.

Câu 38:

Tìm tập xác định D của hàm số $y = \sqrt{(2 - \sqrt{5}) x^{2} + (15 - 7 \sqrt{5}) x + 25 - 10 \sqrt{5}} .$

A. $D = ℝ .$

B. $D = (- \infty; 1) .$

C. $D = [- 5; 1] .$

D. $D = [- 5; \sqrt{5}] .$

Xem đáp án

Hàm số xác định khi và chỉ khi

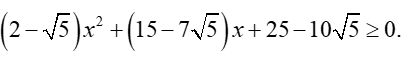
Phương trình

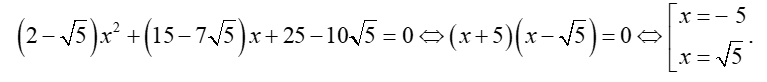
Bảng xét dấu

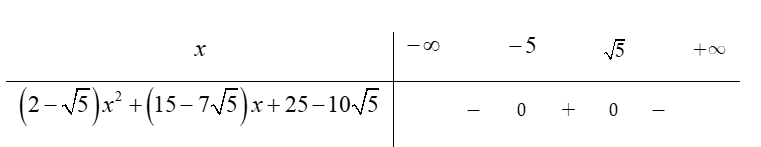
Dựa vào bảng xét dấu ta thấy

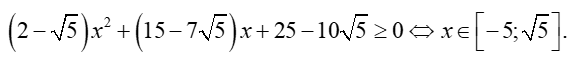
Vậy tâp xác định của hàm số là $D = [- 5; \sqrt{5}]$

Chọn D.

Câu 39:

Tìm tập xác định D của hàm số $y = \frac{3 - x}{\sqrt{4 - 3 x - x^{2}}} .$

A. $D = ℝ \ \{1; - 4\} .$

B. $D = [- 4; 1] .$

C. $D = (- 4; 1) .$

D. $D = (- \infty; 4) \cup (1; + \infty) .$

Xem đáp án

Hàm số xác định khi và chỉ khi

Phương trình

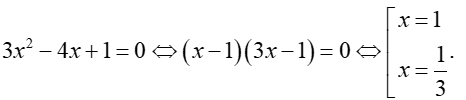
Bảng xét dấu

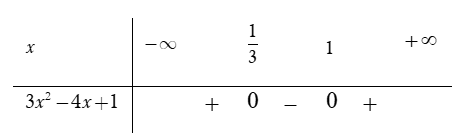
Tìm tập xác định D của hàm số y= 3-x/ căn bậc hai 4-3x-x^2 (ảnh 3)

Dựa vào bảng xét dấu ta thấy

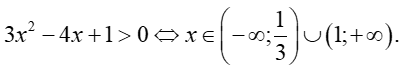
Vậy tập xác định của hàm số là:

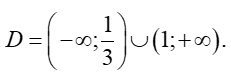
Tìm tập xác định D của hàm số y= 3-x/ căn bậc hai 4-3x-x^2 (ảnh 5)

Chọn C.

Câu 40:

Tìm tập xác định D của hàm số $y = \frac{x^{2} - 1}{\sqrt{3 x^{2} - 4 x + 1}} .$

A. $D = ℝ \ \{1; \frac{1}{3}\} .$

B. $D = (\frac{1}{3}; 1) .$

C. $D = (- \infty; \frac{1}{3}) \cup (1; + \infty) .$

D. $D = (- \infty; \frac{1}{3}] \cup [1; + \infty) .$

Xem đáp án

Hàm số xác định khi và chỉ khi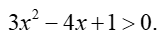

Phương trình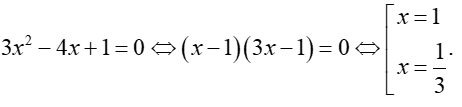

Bảng xét dấu

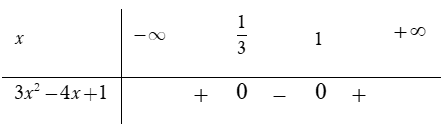
Tìm tập xác định D của hàm số y= x^2-1/căn bậc hai 3x^2-4x+1 (ảnh 3)

Dựa vào bảng xét dấu ta thấy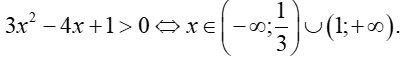

Vậy tập xác định của hàm số là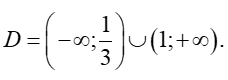

Chọn C.

Câu 41:

Tìm tập xác đinh D của hàm số $y = \sqrt{x^{2} + x - 6} + \frac{1}{\sqrt{x + 4}} .$

A. $D = [- 4; - 3] \cup [2; + \infty) .$

B. $D = (- 4; + \infty) .$

C. $D = (- \infty; - 3] \cup [2; + \infty) .$

D. $D = (- 4; - 3] \cup [2; + \infty) .$

Xem đáp án

Hàm số xác định khi và chỉ khi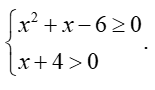

Phương trình 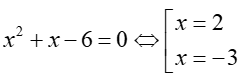và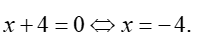

Bảng xét dấu

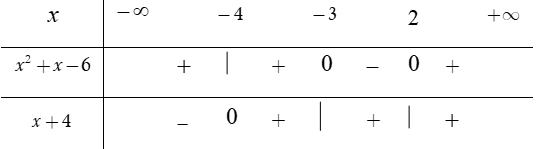
Tìm tập xác đinh D của hàm số y=căn bậc hai x^2+x-6 + 1/ căn bậc hai x+4 (ảnh 4)

Dựa vào bảng xét dấu, ta thấy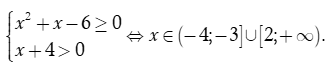

Vậy tập xác định của hàm số là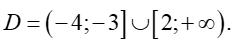

Chọn A.

Câu 42:

Tìm tập xác định D của hàm số $y = \sqrt{x^{2} + 2 x + 3} + \frac{1}{\sqrt{5 - 2 x}} .$

A. $D = [\frac{5}{2}; + \infty) .$

B. $D = (- \infty; \frac{5}{2}] .$

C. $D = (\frac{5}{2}; + \infty) .$

D. $D = (- \infty; \frac{5}{2}) .$

Xem đáp án

Hàm số xác định khi và chỉ khi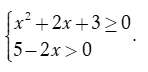

Phương trình 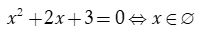và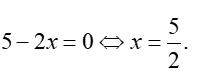

Bảng xét dấu

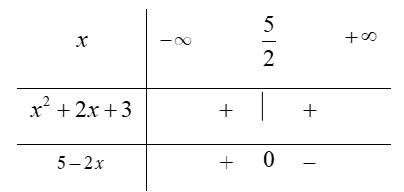
Tìm tập xác định D của hàm số y= căn bậc hai x^2+2x+3+ 1/ căn bậc hai 5-2x (ảnh 4)

Dựa vào bảng xét dấu ta thấy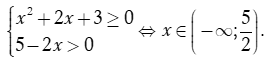

Vậy tập xác định của hàm số là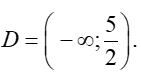

Chọn A.

Câu 43:

Tìm tập xác định D của hàm số $f (x) = \sqrt{\frac{3 - 3 x}{- x^{2} - 2 x + 15} - 1} .$

A. $D = [4; + \infty) .$

B. $D = (- 5; - 3] \cup (3; 4] .$

C. $D = (- \infty; - 5) .$

D. $D = (- 5; 3) \cup (3; 4] .$

Xem đáp án

Hàm số xác định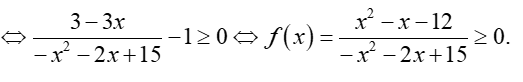

Phương trình 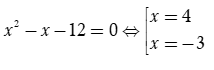và

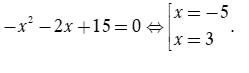
Bảng xét dấu

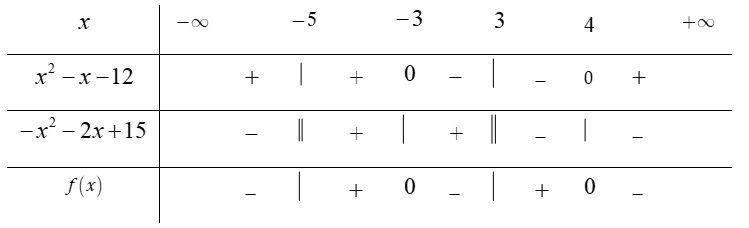
Tìm tập xác định D của hàm số f(x) = căn bậc hai 3-3x/-x^2-2x+15 -1 (ảnh 4)

Dựa vào bảng xét dấu ta thấy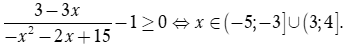

Vậy tập xác định của hàm số là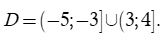

Chọn B.

Câu 44:

Tìm tập xác định D của hàm số $y = \sqrt{\frac{x^{2} + 5 x + 4}{2 x^{2} + 3 x + 1}} .$

A. $D = [- 4; - 1) \cup (- \frac{1}{2}; + \infty) .$

B. $D = (- \infty; - 4] \cup (- 1; - \frac{1}{2}) .$

C. $D = (- \infty; - 4] \cup (- \frac{1}{2}; + \infty) .$

D. $D = [- 4; - \frac{1}{2}) .$

Xem đáp án

Hàm số xác định khi và chỉ khi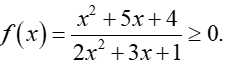

Phương trình 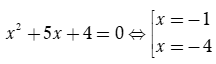và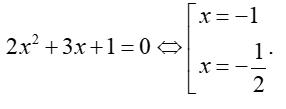

Bảng xét dấu

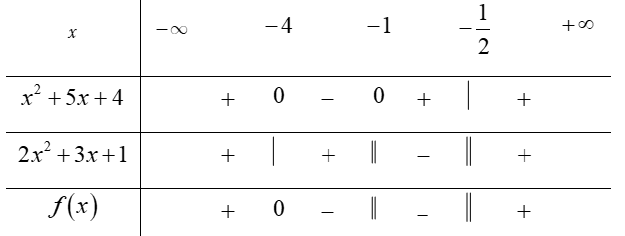
Tìm tập xác định D của hàm số y= căn bậc hai x^2+5x+4/ 2x^2+3x+1 (ảnh 4)

Dựa vào bảng xét dấu ta thấy

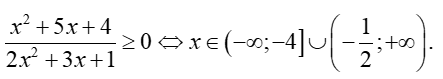
Tìm tập xác định D của hàm số y= căn bậc hai x^2+5x+4/ 2x^2+3x+1 (ảnh 5)

Vậy tập xác định của hàm số là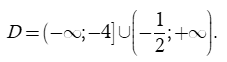

Chọn C.

Câu 45:

Tìm tập xác định D của hàm số $f (x) = \sqrt{\sqrt{x^{2} + x - 12} - 2 \sqrt{2}} .$

A. $D = (- 5; 4] .$

B. $D = (- \infty; - 5) \cup (4; + \infty) .$

C. $D = (- \infty; - 4] \cup [3; + \infty) .$

D. $D = (- \infty; - 5] \cup [4; + \infty) .$

Xem đáp án

Hàm số xác định khi và chỉ khi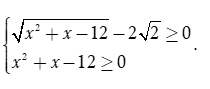

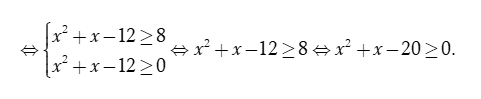
Tìm tập xác định D của hàm số f(x)= căn bậc hai (căn bậc hai x^2+x-12 -2cawn bậc hai 2) (ảnh 2)

Phương trình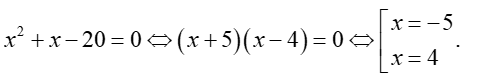

Bảng xét dấu

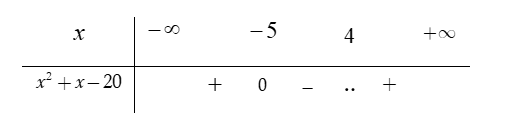
Tìm tập xác định D của hàm số f(x)= căn bậc hai (căn bậc hai x^2+x-12 -2cawn bậc hai 2) (ảnh 4)

Dựa vào bảng xét dấu, ta thấy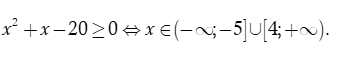

Vậy tập xác định của hàm số là

Chọn B

Câu 46:

Phương trình

x^{2} - (m + 1) x + 1 = 0

vô nghiệm khi và chỉ khi

A. $m > 1.$

B. $- 3 < m < 1.$

C. $m \leq - 3$ hoặc $m \geq 1$

D. $- 3 \leq m \leq 1.$

Xem đáp án

Phương trình vô nghiệm khi và chỉ khi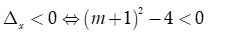

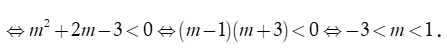
Phương trình x^2-(m+1)x+1=0 vô nghiệm khi và chỉ khi (ảnh 2)

Chọn B.

Câu 47:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình sau vô nghiệm $m = - \frac{1}{2}$

A. $m \in ℝ .$

B. $m > 3.$

C. $m = 3 .$

D. $m > - \frac{3}{5} .$

Xem đáp án

Yêu cầu bài toán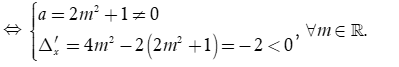

Vậy phương trình đã cho luôn vô nghiệm với mọi $m \in ℝ$

Chọn A.

Câu 48:

Tìm tất cả các giá trị của tham số m để phương trình $(m - 2) x^{2} + 2 (2 m - 3) x + 5 m - 6 = 0$ vô nghiệm ?

A. $m < 0.$

B. $m > 2 .$

C. $[\begin{array}{l} m > 3 \\ m < 1 \end{array} .$

D. $\{\begin{cases} m \neq 2 \\ 1 < m < 3 \end{cases} .$

Xem đáp án

Xét phương trình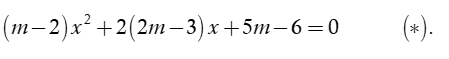

TH1. Với 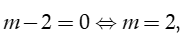khi đó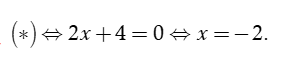

Suy ra với m =2 thì phương trình (*) có nghiệm duy nhất x= -2

Do đó m=2 không thỏa mãn yêu cầu bài toán.

TH2. Với 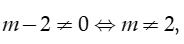khi đó để phương trình (*) vô nghiệm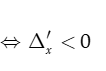

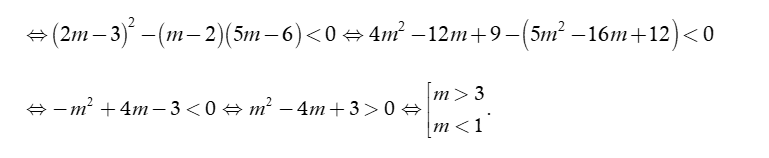
Tìm tất cả các giá trị của tham số m để phương trình (m-2)x^2+2(2m-3)x+5m-6=0 vô nghiệm ? (ảnh 6)

Do đó, với 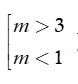thì phương trình (*) vô nghiệm.

Kết hợp hai TH, ta được 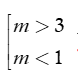là giá trị cần tìm. Chọn C.

Câu 49:

Phương trình $m x^{2} - 2 m x + 4 = 0$ vô nghiệm khi và chỉ khi

A. $0 < m < 4.$

B. $[\begin{array}{l} m < 0 \\ m > 4 \end{array} .$

C. $0 \leq m \leq 4.$

D. $0 \leq m < 4.$

Xem đáp án

Phương trình mx^2-2mx +4=0 vô nghiệm khi và chỉ khi (ảnh 1)

Câu 50:

Phương trình $(m^{2} - 4) x^{2} + 2 (m - 2) x + 3 = 0$ vô nghiệm khi và chỉ khi

A. $m \geq 0.$

B. $m = \pm 2.$

C. $[\begin{array}{l} m \geq 2 \\ m < - 4 \end{array} .$

D. $[\begin{array}{l} m \geq 2 \\ m \leq - 4 \end{array} .$

Xem đáp án

Phương trình (m^2-4)x^2+2(m-2)x+3 vô nghiệm khi và chỉ khi (ảnh 1)

Câu 51:

Cho tam thức bậc hai $f (x) = x^{2} - b x + 3.$ Với giá trị nào của b thì tam thức f(x) có nghiệm ?

A. $b \in [- 2 \sqrt{3}; 2 \sqrt{3}] .$

B. $b \in (- 2 \sqrt{3}; 2 \sqrt{3})$

C. $b \in (- \infty; - 2 \sqrt{3}] \cup [2 \sqrt{3}; + \infty) .$

D. $b \in (- \infty; - 2 \sqrt{3}) \cup (2 \sqrt{3}; + \infty) .$

Xem đáp án

Cho tam thức bậc hai f(x)= x^2-bx+3 Với giá trị nào của b thì tam thức f(x) có nghiệm ? (ảnh 1)

Câu 52:

Phương trình $x^{2} + 2 (m + 2) x - 2 m - 1 = 0$ (m là tham số) có nghiệm khi

A. $[\begin{array}{l} m = - 1 \\ m = - 5 \end{array} .$

B. $- 5 \leq m \leq - 1.$

C. $[\begin{array}{l} m < - 5 \\ m > - 1 \end{array} .$

D. $[\begin{array}{l} m \leq - 5 \\ m \geq - 1 \end{array} .$

Xem đáp án

Phương trình x^2+2(m+2)x-2m-1=0 (m là tham số) có nghiệm khi (ảnh 1)

Câu 53:

Hỏi có tất cả bao nhiêu giá trị nguyên của m để phương trình $2 x^{2} + 2 (m + 2) x + 3 + 4 m + m^{2} = 0$ có nghiệm ?

A. 3

B. 4

C. 2

D. 1

Xem đáp án

Hỏi có tất cả bao nhiêu giá trị nguyên của m để phương trình 2x^2+2(m+2(x+3+4m+m^2=0 (ảnh 1)

Câu 54:

Tìm các giá trị của m để phương trình $(m - 5) x^{2} - 4 m x + m - 2 = 0$ có nghiệm.

A. $m \neq 5.$

B. $- \frac{10}{3} \leq m \leq 1.$

C. $[\begin{array}{l} m \leq - \frac{10}{3} \\ m \geq 1 \end{array} .$

D. $[\begin{array}{l} m \leq - \frac{10}{3} \\ 1 \leq m \neq 5 \end{array} .$

Xem đáp án

Tìm các giá trị của m để phương trình (m-5)x^2-4mx+m-2=0 có nghiệm. (ảnh 1)

Câu 55:

Tìm tất cả giá trị thực của tham số m sao cho phương trình $(m - 1) x^{2} - 2 (m + 3) x - m + 2 = 0$ có nghiệm.

A. $m \in \emptyset .$

B. $m \in ℝ .$

C. $- 1 < m < 3.$

D. $- 2 < m < 2.$

Xem đáp án

Tìm tất cả giá trị thực của tham số m sao cho phương trình (m-1)x^2- 2(m+3)x-m+2=0 (ảnh 1)

Câu 56:

Các giá trị m để tam thức

f (x) = x^{2} - (m + 2) x + 8 m + 1

đổi dấu 2 lần là

A. $m \leq 0$ hoặc $m \geq 28.$

B. $m < 0$ hoặc $m > 28$

C. $0 < m < 28.$

D. $m > 0.$

Xem đáp án

Các giá trị m để tam thức f(x)=x^2-(m+2)x+8m+1 đổi dấu 2 lần là (ảnh 1)

Câu 57:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình $x^{2} + (m + 1) x + m - \frac{1}{3} = 0$ có nghiệm ?

A. $m \in ℝ .$

B. $m > 1.$

C. $- \frac{3}{4} < m < 1.$

D. $m > - \frac{3}{4} .$

Xem đáp án

Tìm tất cả các giá trị thực của tham số m sao cho phương trình x^2+(m+1)x+m-1/3=0 có nghiệm (ảnh 1)

Câu 58:

Tìm tất cả các giá trị của tham số m sao cho phương trình $(m - 1) x^{2} + (3 m - 2) x + 3 - 2 m = 0$ có hai nghiệm phân biệt ?

A. $m \in ℝ .$

B. $2 < m < 6.$

C. $- 1 < m < 6.$

D. $- 1 < m < 2.$

Xem đáp án

Tìm tất cả các giá trị của tham số m sao cho phương trình (m-1)x^2+(3m-2)x+3-2m=0 (ảnh 1)

Câu 59:

Giá trị nào của m=0 thì phương trình $(m - 3) x^{2} + (m + 3) x - (m + 1) = 0$ có hai nghiệm phân biệt ?

A. $m \in (- \infty; - \frac{3}{5}) \cup (1; + \infty) \ \{3\} .$

B. $m \in (- \frac{3}{5}; 1) .$

C. $m \in (- \frac{3}{5}; + \infty) .$

D. $m \in ℝ \ \{3\} .$

Xem đáp án

Giá trị nào của m=0 thì phương trình (m-3)x^2+(m+3)x-(m+1)=0 có hai nghiệm phân biệt (ảnh 1)

Câu 60:

Tìm m để phương trình

x^{2} - m x + m + 3 = 0

có hai nghiệm dương phân biệt.

A. $m > 6.$

B. $m < 6.$

C. $6 > m > 0.$

D. $m > 0.$

Xem đáp án

Tìm m để phương trình x^2-mx+m+3 =0 có hai nghiệm dương phân biệt. (ảnh 1)

Câu 61:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình

(m - 2) x^{2} - 2 m x + m + 3 = 0

có hai nghiệm dương phân biệt.

A. $2 < m < 6.$

B. $m < - 3$ hoặc $2 < m < 6.$

C. $m < 0$ hoặc $- 3 < m < 6.$

D. $- 3 < m < 6.$

Xem đáp án

Tìm tất cả các giá trị thực của tham số m sao cho phương trình (m-2)x^2-2mx+m+3 =0 có hai nghiệm dương phân biệt. (ảnh 1)

Câu 62:

Tìm tất cả các giá trị thực của tham số m để $x^{2} + 2 (m + 1) x + 9 m - 5 = 0$ có hai nghiệm âm phân biệt.

A. $m < 6.$

B. $\frac{5}{9} < m < 1$ hoặc $m > 6.$

C. $m > 1.$

D. $1 < m < 6.$

Xem đáp án

Tìm tất cả các giá trị thực của tham số m để x^2+ 2(m+1)x+9m-5=0 có hai nghiệm âm phân biệt. (ảnh 1)

Câu 63:

Phương trình $x^{2} - (3 m - 2) x + 2 m^{2} - 5 m - 2 = 0$ có hai nghiệm không âm khi

A. $m \in [\frac{2}{3}; + \infty) .$

B. $m \in [\frac{5 + \sqrt{41}}{4}; + \infty) .$

C. $m \in [\frac{2}{3}; \frac{5 + \sqrt{41}}{4}] .$

D. $m \in (- \infty; \frac{5 - \sqrt{41}}{4}] .$

Xem đáp án

Phương trình x^2-(3m-2)x+2m^2-5m-2=0 có hai nghiệm không âm khi (ảnh 1)

Câu 64:

Phương trình $2 x^{2} - (m^{2} - m + 1) x + 2 m^{2} - 3 m - 5 = 0$ có hai nghiệm phân biệt trái dấu khi và chỉ khi

A. $m < - 1$ hoặc $m > \frac{5}{2} .$

B. $- 1 < m < \frac{5}{2} .$

C. $m \leq - 1$ hoặc $m \geq \frac{5}{2} .$

D. $- 1 \leq m \leq \frac{5}{2} .$

Xem đáp án

Câu 65:

Phương trình

(m^{2} - 3 m + 2) x^{2} - 2 m^{2} x - 5 = 0

có hai nghiệm trái dấu khi

A. $m \in (1; 2) .$

B. $m \in (- \infty; 1) \cup (2; + \infty) .$

C. $\{\begin{cases} m \neq 1 \\ m \neq 2 \end{cases} .$

D. $m \in \emptyset .$

Xem đáp án

Phương trình (m^2-3m+2)x^2-2m^2x-5=0 có hai nghiệm trái dấu khi (ảnh 1)

Câu 66:

Giá trị thực của tham số m để phương trình

x^{2} - 2 (m - 1) x + m^{2} - 2 m = 0

có hai nghiệm trái dấu trong đó nghiệm âm có trị tuyệt đối lớn hơn là

A. $0 < m < 2.$

B. $0 < m < 1.$

C. $1 < m < 2.$

D. $[\begin{array}{l} m > 1 \\ m < 0 \end{array} .$

Xem đáp án

Giá trị thực của tham số m để phương trình x^2- 2(m-1)x+m^2-2m=0 (ảnh 1)

Câu 67:

Với giá trị nào của m thì phương trình

(m - 1) x^{2} - 2 (m - 2) x + m - 3 = 0

có hai nghiệm phân biệt

x_{1}, x_{2}

thỏa mãn điều kiện

x_{1} + x_{2} + x_{1} x_{2} < 1

?

A. $1 < m < 2.$

B. $1 < m < 3 .$

C. $m > 2.$

D. $m > 3 .$

Xem đáp án

Với giá trị nào của m thì phương trình (m-1)x^2-2(m-2)x+m-3=0 có hai nghiệm (ảnh 1)

Câu 68:

Tìm giá trị thực của tham số m để phương trình $(m + 1) x^{2} - 2 m x + m - 2 = 0$ có hai nghiệm phân biệt $x_{1}, x_{2}$ khác 0 thỏa mãn $\frac{1}{x_{1}} + \frac{1}{x_{2}} < 3 ?$