Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án - Đề 1
-
1486 lượt thi
-
37 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án: D
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình x2 – (m + 1)x + 1 = 0 vô nghiệm khi và chỉ khi ∆ < 0 ⇔ (m + 1)2 – 4 < 0
⇔ m2 + 2m – 3 < 0 ⇔ – 3 < m < 1.
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bình phương hai vế của phương trình \(\sqrt {4 - 3{x^2}} = 2x - 1\) ta được
4 – 3x2 = 4x2 – 4x + 1.
Sau khi thu gọn ta được 7x2 – 4x – 3 = 0. Từ đó tìm được x = 1 hoặc \(x = - \frac{3}{7}\).
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 1 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 1.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Cách 1. Thay lần lượt các giá trị ở từng đáp án vào cho đến khi tìm được giá trị thỏa mãn.
Cách 2. Giải phương trình
Bình phương hai vế của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \) ta được
3x2 – 6x + 1 = x2 – 3.
Rút gọn ta được x2 – 3x + 2 = 0. Từ đó ta tìm được x = 1 hoặc x = 2.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 14:
 Xem đáp án
Xem đáp án
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án: B
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
\(\overrightarrow c = \overrightarrow a + 3\overrightarrow b \) = (2; – 1) + 3 . (3; 4) = (2; – 1) + (9; 12) = (2 + 9; – 1 + 12) = (11; 11).
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(\cos \left( {\overrightarrow x ,\,\overrightarrow y } \right) = \frac{{\overrightarrow x \cdot \overrightarrow y }}{{\left| {\overrightarrow x } \right| \cdot \left| {\overrightarrow y } \right|}} = \frac{{1.\left( { - 2} \right) + \left( { - 2} \right).\left( { - 6} \right)}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 6} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\).
Do đó, \(\left( {\overrightarrow x ,\,\overrightarrow y } \right) = 45^\circ \).
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 22:
 Xem đáp án
Xem đáp án
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng d: \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = x - 5\\y = - 9 - 2t\end{array} \right.\)⇒ y = – 9 – 2 . (x – 5) ⇔ 2x + y – 1 = 0.
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Khoảng cách từ điểm A(1; 1) đến d: 5x – 12y – 6 = 0 là
\(d\left( {A,\,\,d} \right) = \frac{{\left| {5 \cdot 1 - 12 \cdot 1 - 6} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = 1\).
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng a có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ;\,\, - 1} \right)\);
Đường thẳng b có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1;\, - \sqrt 3 } \right)\).
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
\(\cos \left( {a,\,\,b} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {\sqrt 3 \cdot 1 + \left( { - 1} \right) \cdot \left( { - \sqrt 3 } \right)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} \cdot \sqrt {{1^2} + {{\left( { - \sqrt 3 } \right)}^2}} }} = \frac{{\sqrt 3 }}{2}\).
Suy ra góc giữa hai đường thẳng bằng 30°.
Câu 28:
 Xem đáp án
Xem đáp án
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 nên bán kính đường tròn chính là khoảng cách từ tâm I đến đường thẳng ∆.
Ta có: R = d(I, ∆) = \(\frac{{\left| {3 \cdot 3 + 4 \cdot 4 - 10} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 3\).
Vậy phương trình đường tròn cần tìm là: (x – 3)2 + (y – 4)2 = 9.
Câu 30:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn (C) có tâm là I(2; – 2). Tiếp tuyến của (C) tại M(1; 0) có vectơ pháp tuyến \(\overrightarrow {MI} = \left( {1;\, - 2} \right)\), nên có phương trình
1(x – 1) – 2(y – 0) = 0 hay x – 2y – 1 = 0.
Câu 31:
 Xem đáp án
Xem đáp án
Đáp án: D
Câu 32:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 34:
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\,\,\left( {a,\,b > 0} \right)\).
Từ giả thiết ta có: \(\left\{ \begin{array}{l}\frac{c}{a} = 2\\2c = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = 2\end{array} \right. \Rightarrow b = \sqrt {{2^2} - {1^2}} = \sqrt 3 \).
Vậy (H) có phương trình là: \(\frac{{{x^2}}}{{{1^2}}} - \frac{{{y^2}}}{{{{\left( {\sqrt 3 } \right)}^2}}} = 1\,\,\,hay\,\,\,{x^2} - \frac{{{y^2}}}{3} = 1\).
Câu 36:
 Xem đáp án
Xem đáp án
Đáp án:
Gọi tọa độ các điểm A, B và M là A(xA; yA); B(xB; yB) và M(xM; yM).
Vì A thuộc d1 nên 2xA – yA – 2 = 0. Suy ra yA = 2xA – 2.
Vì B thuộc d2 nên xB + yB + 3 = 0. Suy ra yB = – xB – 3.
Do M là trung điểm của đoạn AB nên
\(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 6\\\left( {2{x_A} - 2} \right) + \left( { - {x_B} - 3} \right) = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} = \frac{{11}}{3}\\{y_A} = \frac{{16}}{3}\end{array} \right.\).
Suy ra \(A\left( {\frac{{11}}{3};\,\,\frac{{16}}{3}} \right)\).
Đường thẳng ∆ đi qua điểm A và điểm M.
Ta có: \(\overrightarrow {AM} = \left( { - \frac{2}{3};\,\, - \frac{{16}}{3}} \right)\)\( \Rightarrow \overrightarrow {{u_{AM}}} = \left( {1;\,\,8} \right) \Rightarrow \overrightarrow {{n_{AM}}} = \left( {8;\,\, - 1} \right)\).
Đường thẳng ∆ đi qua M(3; 0) và có một vectơ pháp tuyến là \(\overrightarrow {{n_{AM}}} \) nên có phương trình là
8(x – 3) – (y – 0) = 0 hay 8x – y – 24 = 0.
Câu 37:
 Xem đáp án
Xem đáp án
Đáp án:
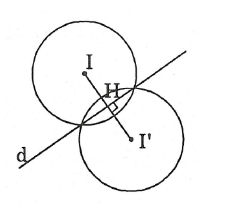
(C) có tâm I(1; 2), bán kính R = 2.
Phương trình đường thẳng ∆ đi qua I, vuông góc với d có dạng x + y + m = 0.
I (1; 2) ∈ ∆, suy ra 1 + 2 + m = 0 ⇒ m = – 3.
Do đó, phương trình đường thẳng ∆: x + y – 3 = 0.
Gọi H là giao điểm của ∆ và d. Tọa độ của H là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}{\rm{x}} + {\rm{y}} - 3 = 0\\{\rm{x}} - {\rm{y}} - 1 = 0\end{array} \right.\]
Từ đó tìm được H(2; 1).
Chứng minh được H là trung điểm của II' với I' là tâm của (C'). Suy ra I'(3; 0)
Vì (C), (C') đối xứng nhau qua d nên R = R'.
Vậy phương trình (C'): (x – 3)2 + y2 = 4.
Tọa độ giao điểm của (C), (C') là nghiệm của hệ phương trình:
\[\left\{ \begin{array}{l}{\left( {{\rm{x}} - 1} \right)^2} + {\left( {{\rm{y}} - 2} \right)^2} = 4\\{\left( {{\rm{x}} - 3} \right)^2} + {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {{\rm{x}} - 1} \right)^2} + {\left( {{\rm{y}} - 2} \right)^2} = 4\\{\rm{x}} - {\rm{y}} - 1 = 0\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}{{\rm{x}}_{\rm{1}}} = 1 \Rightarrow {{\rm{y}}_{\rm{1}}} = 0\\{{\rm{x}}_{\rm{2}}} = 3 \Rightarrow {{\rm{y}}_2} = 2\end{array} \right. \Rightarrow {\rm{A}}\left( {1;0} \right),\,\,{\rm{B}}\left( {3;2} \right)\] là giao điểm của (C), (C').
