Trắc nghiệm Toán 10 Bài 1. Quy tắc cộng và quy tắc nhân có đáp án
-
1000 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi đến nhà Cường?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ nhà An đến nhà Bình có 4 cách chọn đường.
Từ nhà Bình đến nhà Cường có 6 cách chọn đường.
Áp dụng quy tắc nhân ta có số cách chọn đường đi từ nhà An đến nhà Cường là: 4.6 = 24 (cách).
Câu 2:
Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Chọn 1 cái bút có 10 cách
Chọn 1 quyển sách có 8 cách.
Vậy theo quy tắc nhân, số cách chọn 1 cái bút và 1 quyển sách là: 10.8 = 80 cách.
Câu 3:
Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
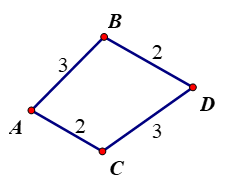
Đi từ thành phố A đến thành phố D ta có các trường hợp sau:
Trường hợp 1. Đi từ thành phố A đến thành phố B rồi đến thành phố D
Ta có: đi là từ thành phố A đến thành phố B có 3 cách, đi là từ thành phố B đến thành phố D có 2 cách
Vậy trường hợp 1 có 3.2 = 6 cách
Trường hợp 2. Đi từ thành phố A đến thành phố C rồi đến thành phố D
Ta có: đi là từ thành phố A đến thành phố C có 2 cách ,đi là từ thành phố C đến thành phố D có 3 cách
Vậy trường hợp 2 có 2.3 = 6 cách
Để đi từ thành phố A đến thành phố D ta có 6 + 6 = 12 cách.
Câu 4:
Cho các chữ số 2, 3, 4, 5, 6, 7, 8, 9 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi số tự nhiên có 3 chữ số cần tìm là: \[\overline {abc} \] (a ≠ 0) khi đó
chọn số c có 4 cách chọn ( vì \[\overline {abc} \] là số chẵn nên c chỉ có thể chọn một trong các số 2, 4, 6, 8)
chọn số a có 8 cách chọn (vì a được chọn tuỳ ý nên a có thể chọn một trong 8 số 2, 3, 4, 5, 6, 7, 8, 9)
chọn số b có 8 cách chọn (vì b được chọn tuỳ ý nên b có thể chọn một trong 8 số 2, 3, 4, 5, 6, 7, 8, 9)
Vậy số các số tự nhiên chẵn có 3 chữ số là được lập từ các số trên là: 8.8.4 = 256 (số)
Câu 5:
Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số khác nhau?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi số có ba chữ số cần tìm là \[\overline {abc} \], với a ≠ 0
Trường hợp 1: c = 0
Chọn số c có 1cách
Chọn số a có 6 cách (vì a ≠ 0 nên a có thể chọn một trong 6 số là 1; 2; 3; 4; 5; 6)
Chọn số b có 5 cách (vì b ≠ a, b ≠ c nên b còn 5 cách chọn)
Vậy có 6.5.1 = 30 số
Trường hợp 2: c ≠ 0
Chọn c có 3 cách chọn (vì số \[\overline {abc} \] là số chẵn nên c có thể chọn một trong 3 số là 2; 4; 6)
Chọn số a có 5 cách chọn (vì a ≠ 0 và a ≠ c nên a có 5 cách chọn)
Chọn số b có 5 cách chọn(vì b ≠ a, b ≠ c nên b còn 5 cách chọn)
Vậy có 5.5.3 = 75 số
Số các số tự nhiên chẵn có 3 chữ số khác nhau lập từ các số trên là: 75 + 30 = 105.
Câu 6:
Bạn Dũng có 9 quyển truyện tranh khác nhau và 6 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Sách bạn Dũng có thể lấy ra thuộc hai loại: Truyện tranh hoặc tiểu thuyết.
Truyện tranh: 9 quyển
Tiểu thuyết: 6 quyển
Số cách Dũng lấy ra một quyển là: 9 + 6 = 15 (cách)
Câu 7:
Cho các số 1; 2; 3; 4; 5; 6; 7. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau lấy từ 7 chữ số trên sao cho chữ số đầu tiên là số 3
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi số cần tìm có dạng: \(\overline {abcde} \), a ≠ 0.
Chọn số a có 1 cách chọn ( vì chữ số bắt đầu bằng số 3 nên a chỉ có 1 cách chọn là số 3)
Chọn số b có 6 cách chọn (vì b ≠ a nên b còn 6 số để chọn)
Chọn số c có 5 cách chọn (vì c ≠ a, c ≠ b nên c còn 5 số để chọn)
Chọn số d có 4 cách chọn (vì d ≠ a, d ≠ b, d ≠ c nên d còn 4 số để chọn)
Chọn số e có 3 cách chọn (vì e ≠ a, e ≠ b, e ≠ c, e ≠ d nên e còn 3 số để chọn)
Số các số tự nhiên gồm 5 chữ số khác lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3 là: 1.6.5.4.3 = 360 (số).
Câu 8:
Có bao nhiêu số chẵn gồm bốn chữ số được lập từ các số 0; 1; 2; 4; 5; 6; 8.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B.
Gọi số cần tìm có dạng: \(\overline {abcd} \), a ≠ 0
Chọn d có 5 cách chọn (vì \(\overline {abcd} \) là số chẵn nên d có thể chọn một trong các số 0; 2; 4; 6; 8)
Chọn a có 6 cách chọn (vì a có thể chọn tuỳ ý một trong các số 1; 2; 4; 5; 6; 8)
Chọn b có 7 cách chọn (vì b có thể chọn tuỳ ý một trong các số 0; 1; 2; 4; 5; 6; 8)
Chọn c có 7 cách chọn (vì c có thể chọn tuỳ ý một trong các số 0; 1; 2; 4; 5; 6; 8)
Vậy có 6.7.7.5 = 1470.
Câu 9:
Có bao nhiêu số tự nhiên gồm 5 chữ số chia hết cho 5
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi số cần tìm có dạng : \(\overline {abcde} \), a ≠ 0
Chọn số e có 2 cách chọn (vì số \(\overline {abcde} \) chia hết cho 5 nên e chỉ có thể chọn là số 0 hoặc 5)
Chọn số a có 9 cách chọn (vì a ≠ 0 nên a chỉ được chọn một trong 9 số 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Chọn số b có 10 cách chọn (vì b chọn tuỳ ý nên b có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Chọn số c có 10 cách chọn (vì c chọn tuỳ ý nên c có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Chọn số d có 10 cách chọn (vì d chọn tuỳ ý nên d có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Tổng kết, theo quy tắc nhân ta có Số các số tự nhiên gồm 5 chữ số chia hết cho 10 là: 2.9.10.10.10 = 18000 (số)
Câu 10:
Có bao nhiêu cách sắp xếp 3 nữ sinh và 3 nam sinh thành một hàng dọc sao cho các bạn nam đứng cạnh nhau và nữ đứng cạnh nhau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Trường hợp 1: nữ đứng trước
Có 6 vị trí để xếp, vì nam đứng cạnh nhau và nữ đứng cạnh nhau nên nữ sẽ đứng vị trí số 1, 2, 3 còn nam đứng vị trí số 4, 5, 6
Sắp xếp học sinh nữ vào vị trí 1, 2, 3
Vị trí số 1 có 3 cách chọn (vì có thể chọn một bạn bất kỳ trong 3 bạn nữ)
Vị trí số 2 có 2 cách chọn (vì chỉ có thể chọn một trong hai bạn nữ còn lại)
Vị trí số 3 có 1 cách chọn (vì chỉ còn 1 bạn nữ để chọn)
Có 6 vị trí để xếp, vì nam nữ đứng xen kẽ nên nữ sẽ đứng vị trí số 1, 3, 5 còn nam đứng vị trí số 2, 4, 6.
Sắp xếp học sinh nam vào vị trí 4, 5, 6
Vị trí số 4 có 3 cách chọn (vì có thể chọn một bạn bất kỳ trong 3 bạn nam)
Vị trí số 5 có 2 cách chọn (vì chỉ có thể chọn một trong hai bạn nam còn lại)
Vị trí số 6 có 1 cách chọn (vì chỉ còn 1 bạn nam để chọn)
Trường hợp 1 có 3.2.1.3.2.1 = 36 (cách xếp)
Trường hợp 2, nam đứng trước
Tương tự như trường hợp 1, trường hợp 2 có 36 (cách xếp)
Vậy áp dụng quy tắc cộng ta có cả hai trường hợp có 36 + 36 = 72 (cách xếp)
Câu 11:
Một liên đoàn bóng đá có 10 đội, mỗi đội phải đá 4 trận với mỗi đội khác, 2 trận ở sân nhà và 2 trận ở sân khách. Số trận đấu được sắp xếp là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Mỗi đội sẽ gặp 9 đội khác trong hai lượt trận sân nhà và sân khách. Có 10.9 = 9 trận.
Mỗi đội đá 2 trận sân nhà, 2 trận sân khách. Nên số trận đấu là 2.90 =180 trận.
Câu 12:
Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì số có chín chữ số viết theo thứ tự giảm dần nên chỉ có thể là chữ số 9 hoặc chữ số 8 đứng đầu.
Trường hợp 1, số 9 đứng đầu
Từ các số 0; 1; 2; 3; 4; 5; 6; 7; 8 mỗi một lần ta bỏ đi một số ta sẽ lập được 1 số có 9 chữ số viết theo thứ tự giảm dần mà số 9 đứng đầu.
Vậy trường hợp 1 có 9 số được lập
Trường hợp 2, số 8 đứng đầu
Vì từ 0 đến 8 có chín chữ số nên ta chỉ lập được 1 số có 9 chữ số viết theo thứ tự giảm đần
Vậy cả 2 trường hợp có 9 + 1 = 10 số
Câu 13:
Từ các chữ số 0; 2; 5; 3; 6; 8 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau trong đó hai chữ số 0 và 5 không đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi số cần tìm là \(\overline {abcdef} \) a ≠ 0
Số có 6 chữ số khác nhau được lập từ các số trên
Chọn số a có 5 cách( vì a có thể chọn một trong 5 số 2; 3; 5; 6; 8)
Chọn b có 5 cách (vì b ≠ a nên b có thể chọn một trong các số 0; 2; 5; 3; 6; 8 nhưng bỏ đi số a đã chọn)
Chọn c có 4 cách (vì các chữ số khác nhau nên c không được chọn số a và b đã chọn)
Chọn d có 3 cách (vì các chữ số khác nhau nên d không được chọn số a, b, c đã chọn)
Chọn e có 2 cách (vì các chữ số khác nhau nên e không được chọn số a, b, c, d đã chọn)
Chọn f có 1 cách (vì các chữ số khác nhau nên f không được chọn số a, b, c, d, e đã chọn)
Vậy có 5.5.4.3.2.1 = 600 số
Số các số có 6 chữ số khác nhau mà 5 và 0 đứng cạnh nhau là
Trường hợp 1, số 5 đứng trước số 0
Vì 5 và 0 đứng cạnh nhau nên ta coi là 1 vị trí xếp số có 6 chữ số lúc này có 5 vị trí để xếp và các chữ số khác nhau nên số cách chọn lần lượt là 5, 4, 3, 2, 1 cách
Vậy có 5.4.3.2.1 = 120 số
Trường hợp 2, số 0 đứng trước số 5
Vì a ≠ 0 nên a có 4 cách chọn(a có thể chọn 1 trong 4 số 2, 3, 6, 8)
Vì 0 và 5 đứng cạnh nhau nên ta coi là 1 vị trí xếp số có 6 chữ số lúc này có 4 vị trí để xếp và các chữ số khác nhau nên số cách chọn lần lượt là 4, 3, 2, 1 cách
Vậy có 4.4.3.2.1 = 96 số
Số các số có 6 chữ số khác nhau mà 5 và 0 đứng cạnh nhau là 120 + 96 = 216 số
Số các số có 6 chữ số khác nhau mà 5 và 0 không đứng cạnh nhau là 600 – 216 = 384 số
Câu 14:
Từ các chữ số 0; 1; 2; 3; 4; 5; 8 lập được bao nhiêu số có ba chữ số đôi một khác nhau, chia hết cho 2 và 3.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Số chia hết cho 2 và 3 là số chẵn và có tổng các chữ số của nó chia hết cho 3.
Gọi \[\overline {abc} \]là số tự nhiên có ba chữ số đôi một khác nhau, chia hết cho 2 và 3 được lập từ các chữ số 0; 1; 2; 3; 4; 5; 8
Trường hợp 1: c = 0
Khi đó các chữ số a, b được lập từ các tập{1; 2}; {1; 5}; {1; 8}; {2; 4}; {4; 5}; {4; 8}
Có 6 cặp số a, b mỗi cặp lập được 2 số nên có 6.2 = 12 số.
Trường hợp 2: c = 2
Khi đó các chữ số a, b được lập từ các tập {1; 0}; {4; 0}; {1; 3}; {3; 4}; {5; 8}
Cặp số {1; 0}; {4; 0} mỗi cặp lập được một số, cặp {1; 3}; {3; 4}; {5; 8} mỗi cặp lập được 2 số nên ta có 2 + 3.2 = 8 số
Trường hợp 3: c = 4
Khi đó các chữ số a, b được lập từ các tập {2; 0}; {2; 3}; {3; 5}; {3; 8}
Cặp số {2; 0} lập được một số, cặp {2; 3}; {3; 5}; {3; 8} mỗi cặp lập được 2 số nên ta có 1 + 3.2 = 7 số
Trường hợp 4: c = 8
Khi đó các chữ số a, b được lập từ các tập {0; 1}; {0; 4}; {1; 3}; {2; 5}; {3; 4}
Cặp số {0; 1}; {0; 4} mỗi cặp lập được một số, cặp {1; 3}; {2; 5}; {3; 4} mỗi cặp lập được 2 số nên ta có 2 + 3.2 = 8 số
Vậy có tất cả 12 + 8 + 7 + 8 = 35 số
Câu 15:
Trên giá sách có 7 quyển sách Tiếng Nga khác nhau, 9 quyển sách Tiếng Anh khác nhau và 8 quyển sách Tiếng Việt khác nhau. Số cách chọn hai quyển sách khác loại là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì có 3 loại sách khác nhau mà chỉ cần chọn ra 2 quyển khác loại nên ta có các trường hợp sau
Trường hợp 1: Chọn được sách Tiếng Nga và Tiếng Anh, vì chọn 2 quyển khác loại nên mỗi loại sách chỉ được chọn 1 quyển ta có:
Tiếng Nga có 7 cách chọn
Tiếng Anh có 9 cách chọn
Vậy số cách chọn 2 quyển sách khác loại là: 7.9 = 63 (cách)
Trường hợp 2: Chọn được sách Tiếng Nga và Tiếng Việt, vì chọn 2 quyển khác loại nên mỗi loại sách chỉ được chọn 1 quyển ta có:
Tiếng Nga có 9 cách chọn
Tiếng Việt có 8 cách chọn
Vậy số cách chọn 2 quyển sách khác loại là 9.8 = 72 (cách)
Trường hợp 3: Chọn được sách Tiếng Anh và Tiếng Việt, vì chọn 2 quyển khác loại nên mỗi loại sách chỉ được chọn 1 quyển ta có:
Tiếng Anh có 7 cách chọn
Tiếng Việt có 8 cách chọn
Vậy số cách chọn 2 quyển sách khác loại là 7.8 = 56 cách
Tổng kết, áp dụng quy tắc cộng ta có số cách chọn hai quyển sách khác loại trong 3 loại trên là: 63 + 72 + 56 = 191 (cách).
