50 câu trắc nghiệm Hàm số bậc nhất và bậc hai nâng cao (P1)
-
7300 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Xét tính chẵn, lẻ của hai hàm số:
 Xem đáp án
Xem đáp án
Đáp án B
+ Hàm số f(x) và g(x) đều có tập xác định là D= R.
+ Xét hàm số y=f(x) : Với mọi và
Nên y= f(x) là hàm số lẻ.
+ Xét hàm số y = g(x) :
Với mọi nên y = g(x) là hàm số chẵn.
Chọn B.
Câu 5:
Hàm số có tập xác định là:
 Xem đáp án
Xem đáp án
Đáp án A
+ Hàm số xác định khi và chỉ khi:
Do đó tập xác định là
+ Do đó tập xác định của hàm số đã cho là
Chọn A.
Câu 6:
Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua C( 3; -2) và song song với ∆: 3x-2y+1=0
 Xem đáp án
Xem đáp án
Chọn D.
Câu 7:
Cho hàm số bậc nhất có đồ thị là đường thẳng d.Tìm hàm số đó biết d đi qua M(1;2) và cắt hai tia Ox;Oy tại P và Q sao cho nhỏ nhất
 Xem đáp án
Xem đáp án
Đáp án B
Gọi hàm số cần tìm là y= ax+ b.
Đường thẳng d cắt trục Ox tại và cắt Oy tại Q(0; b) với a<0 và b> 0
Suy ra
Ta có d đi qua M nên 2= a+b hay b= 2-a thay vào (3) ta được
Áp dụng bất đẳng thức côsi ta có
Đẳng thức xảy ra khi và chỉ khi
Vậy hàm số cần tìm là y= -2x+ 4.
Câu 8:
Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua N(2; -1) và
 Xem đáp án
Xem đáp án
Đáp án D
Chọn D
Câu 10:
Cho hai đường thẳng d: y= x+ 2m và d’: y= 3x+2 ( m là tham số). Có mấy giá trị của m để ba đường thẳng d; d’ và d’’: y= -mx+ 2 phân biệt đồng quy.
 Xem đáp án
Xem đáp án
Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.
Câu 11:
Cho đường thẳng d: y= (m-1) x+m và d’: y= (m2-1) x+ 6 . Có bao nhiêu giá trị của m để hai đường thẳng d; d’ song song với nhau.
 Xem đáp án
Xem đáp án
Đáp án C
+Với m=1 ta có d: y=1 và d’: y=6
do đó hai đường thẳng này song song với nhau.
+ Với m =-1 ta có d: y= -2x-1 và d’: y= 6
suy ra hai đường thẳng này cắt nhau tại M(-7/2; 6)
+ Với m ≠ ± 1 khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi:
Đối chiếu với điều kiện m≠± 1 suy ra m= 0.
Vậy m= 0 và m= 1 là giá trị cần tìm.
Chọn C.
Câu 12:
Cho đường thẳng d: y= (m-1) x+m và d’: y= (m2-1) x+ 6 . Tìm m để đường thẳng d cắt trục tung tại A, d’ cắt trục hoành tại B sao cho tam giác OAB cân tại O?
 Xem đáp án
Xem đáp án
Đáp án D
Chọn D.
Câu 13:
Cho hàm số . Trên đồ thị của hàm số lấy hai điểm A và B hoành độ lần lượt là - 2 và 1. Phương trình đường thẳng AB là:
 Xem đáp án
Xem đáp án
Đáp án A
Câu 14:
Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua M( 1;2) và cắt hai tia Ox; Oy tại P và Q sao cho tam giác OPQ cân tại O.
 Xem đáp án
Xem đáp án
Đáp án D
Gọi hàm số cần tìm là y= ax + b
Đường thẳng d cắt trục Ox tại và cắt Oy tại Q( 0 ;b) với a< 0; b> 0
Ta có tam giác OPQ cân tại O nên hay b( a+1) =0
Suy ra b=0 (loại) hoặc a= -1
Ta có d qua M nên 2=a+ b nên b= 3
Vậy hàm số cần tìm là y= -x+ 3.
Chọn D.
Câu 15:
Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua N( 1; -1) và
 Xem đáp án
Xem đáp án
Gọi d: y=ax+ b
Đường thẳng d đi qua N( 1; -1) nên -1= a+ b
Và suy ra b= -2.
Vậy hàm số cần tìm là y= x-2.
Chọn B.
Câu 16:
Các đường thẳng y= -5( x+ 1) ; y= 3x+a và y=ax+3 đồng quy khi a= ?
 Xem đáp án
Xem đáp án
+ Phương trình hoành độ giao điểm giữa hai đường thẳng y= -5( x+ 1) và y=3x+a :
-5x-5=3x+a suy ra -8x-a=5 (1)
+ Phương trình hoành độ giao điểm giữa hai đường thẳng y= 3x+a và y=ax+3là:
ax+3=3x+a hay (a-3) x=a-3
suy ra x=1( vì a≠3).
+Thế x= 1 vào (1) ta được: -8-a=5 nên a= -13.
Chọn D.
Câu 17:
Tính tổng tất cả các giá trị của m để ba đường thẳng d: y= 2x; d’: y= -x+6 và d’’: y=m2x +5m+3 phân biệt đồng quy.
 Xem đáp án
Xem đáp án
Tọa độ giao điểm(nếu có) của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
suy ra d và d’ cắt nhau tại M(2; 4).
Vì ba đường thẳng đã cho đồng quy nên d’’ đi qua M ta có
Kiểm tra lại với ba đường thẳng đó phân biệt và đồng quy
Vậy là giá trị cần tìm và tổng 2 giá trị đó là -5/2.
Chọn C.
Câu 18:
Tồn tại giá trị của m để hai đường thẳng sau cắt nhau tại một điểm trên trục hoành: (m-1) x+ my-5=0 và mx+ (2m-1)y + 7=0. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
+ Hai đường thẳng cắt nhau tại một điểm trên trục hoành suy ra tung độ giao điểm là y=0.
+ Từ đây ta có: (m-1)x-5=9 suy ra
Đồng thời: mx+7=0 suy ra x= -7/m ( m≠0) (2)
+ Từ (1) và (2) ta có:
Chọn D.
Câu 22:
Cho hàm số Bảng biến thiên nào sau đây là bảng biến thiên của hàm số đã cho.
 Xem đáp án
Xem đáp án
Suy ra hàm số đồng biến khi x≥ 2, nghịch biến khi x< 2.
Chọn D.
Câu 23:
Hàm số y = |x|+2 có bảng biến thiên nào sau đây:
 Xem đáp án
Xem đáp án
Suy ra hàm số đồng biến khi x≥ 0, nghịch biến khi x< 0.
Chọn C.
Câu 24:
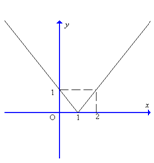
Đồ thị sau đây biểu diễn hàm số nào?
 Xem đáp án
Xem đáp án
+Khi x≥ 1 đồ thị hàm số là đường thẳng đi qua hai điểm (1; 0) và (2;1) nên hàm số cần tìm trong trường hợp này là y= x-1.
+Khi x< 1 đồ thị hàm số là đường thẳng đi qua hai điểm (1; 0) và (0;1) nên hàm số cần tìm trong trường hợp này là y= -x+1.
Vậy hàm số cần tìm là
Chọn B.
Câu 25:
Cho hàm số y= 2x-3 có đồ thị là đường thẳng ∆. Đường thẳng ∆ tạo với hai trục tọa độ một tam giác có diện tích bằng:
 Xem đáp án
Xem đáp án
+ Giao điểm của đồ thị hàm số y= 2x-3 với trục hoành là điểm A( 3/2; 0).
+ Giao điểm của đồ thị hàm số y= 2x-3 với trục tung là điểm B( 0; -3).
+ Đường thẳng ∆ tạo với hai trục tọa độ ∆ OAB vuông tại O. Suy ra
Chọn B.