15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 3. Tích của một số với một vectơ có đáp án

Câu 1:

Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính độ dài $\vec{C B} + \vec{A B}$ .

A. $\sqrt{13}$

B. $2 \sqrt{13}$

C. $2 \sqrt{3}$

D. $\sqrt{3}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

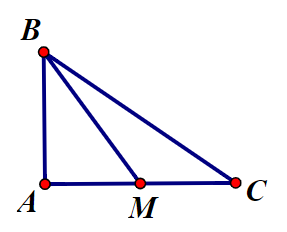
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính độ dài vecto CB+AB (ảnh 1)

Gọi M là trung điểm AC, ta suy ra $\vec{M A} + \vec{M C} = \vec{0}$ .

\Leftrightarrow - \vec{A M} - \vec{C M} = \vec{0}

\Leftrightarrow - (\vec{A M} + \vec{C M}) = \vec{0}

\Leftrightarrow \vec{A M} + \vec{C M} = \vec{0}

Ta có $\vec{C B} + \vec{A B} = \vec{C M} + \vec{M B} + \vec{A M} + \vec{M B} = (\vec{A M} + \vec{C M}) + 2 \vec{M B} = \vec{0} + 2 \vec{M B} = 2 \vec{M B}$ .

Vì M là trung điểm AC nên AM = $\frac{A C}{2}$ = 2.

Tam giác ABM vuông tại A: $B M^{2} = A B^{2} + A M^{2}$ (Định lý Pytago)

\Leftrightarrow B M^{2} = 3^{2} + 2^{2} = 13

\Rightarrow B M = \sqrt{13}

Ta suy ra $|\vec{C B} + \vec{A B}| = |2 \vec{M B}| = 2. M B = 2 \sqrt{13}$ .

Vậy ta chọn đáp án B.

Câu 2:

Cho $\vec{a} \neq \vec{0}$ và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn $\vec{O M} = 3 \vec{a}$ và $\vec{O N} = - 4 \vec{a}$ . Tìm $\vec{M N}$ .

A. $\vec{M N} = 7 \vec{a}$

B. $\vec{M N} = 5 \vec{a}$

C. $\vec{M N} = - 7 \vec{a}$

D. $\vec{M N} = - 5 \vec{a}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có $\vec{M N} = \vec{O N} - \vec{O M} = - 4 \vec{a} - 3 \vec{a} = - 7 \vec{a}$ .

Câu 3:

Cho tam giác ABC có trọng tâm G. Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Trong các khẳng định sau, khẳng định nào đúng?

A. $\vec{A G} = \frac{1}{2} \vec{A E} + \frac{1}{2} \vec{AF}$

B. $\vec{A G} = \frac{1}{3} \vec{A E} + \frac{1}{3} \vec{AF}$

C. $\vec{A G} = \frac{3}{2} \vec{A E} + \frac{3}{2} \vec{AF}$

D. $\vec{A G} = \frac{2}{3} \vec{A E} + \frac{2}{3} \vec{AF}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

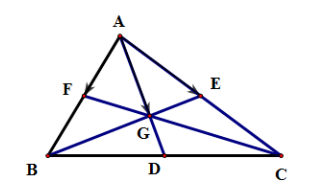
Vì G là trọng tâm của tam giác ABC nên ta có $\vec{A G} = \frac{2}{3} \vec{A D}$ .

Tam giác ABC có D là trung điểm cạnh BC, suy ra $2 \vec{A D} = \vec{A B} + \vec{A C}$ .

Ta có E, F lần lượt là trung điểm AC, AB.

Suy ra $\vec{A C} = 2 \vec{A E}$ và $\vec{A B} = 2 \vec{A F}$ .

Khi đó ta có $\vec{A G} = \frac{2}{3} \vec{A D} = \frac{1}{3} (\vec{A B} + \vec{A C}) = \frac{1}{3} (2 \vec{A F} + 2 \vec{A E}) = \frac{2}{3} \vec{A E} + \frac{2}{3} \vec{A F}$ .

Vậy ta chọn đáp án D.

Câu 4:

Cho ba điểm phân biệt A, B, C. Nếu $\vec{A B} = - 3 \vec{A C}$ thì đẳng thức nào dưới đây đúng?

A. $\vec{B C} = - 4 \vec{A C}$

B. $\vec{B C} = - 2 \vec{A C}$

C. $\vec{B C} = 2 \vec{A C}$

D. $\vec{B C} = 4 \vec{A C}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Từ đẳng thức $\vec{A B} = - 3 \vec{A C}$ , ta suy ra ba điểm A, B, C thẳng hàng.

Vì k = – 3 < 0 nên $\vec{A B}$ và $\vec{A C}$ ngược hướng. Do đó điểm A nằm giữa hai điểm B và C.

Ta có $\vec{A B} = - 3 \vec{A C}$ , suy ra $|\vec{A B}| = |- 3 \vec{A C}|$ , do đó AB = 3AC.

Suy ra BC = AB + AC = 3AC + AC = 4AC.

Mà $\vec{B C}, \vec{A C}$ cùng hướng.

Do đó ta suy ra $\vec{B C} = 4 \vec{A C}$ .

Vậy ta chọn đáp án D.

Câu 5:

Cho hình bình hành ABCD tâm O. Mệnh đề nào sau đây là sai?

A. $\vec{A B} + \vec{A D} = \vec{A C}$

B. $\vec{O A} = \frac{1}{2} (\vec{B A} + \vec{C B})$

C. $\vec{O A} + \vec{O B} = \vec{O C} + \vec{O D}$

D. $\vec{O A} + \vec{O B} = \vec{D A}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

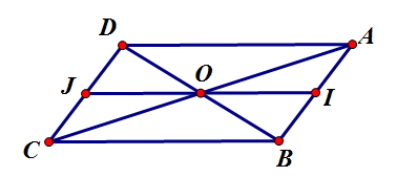
Ta xét từng đáp án:

Đáp án A: Theo quy tắc hình bình hành, ta có $\vec{A B} + \vec{A D} = \vec{A C}$ ⇒ A đúng.

Đáp án B: Vì O là tâm của hình bình hành ABCD nên O là trung điểm AC.

Ta suy ra $O A = \frac{1}{2} C A$ .

Mà $\vec{O A}, \vec{C A}$ cùng hướng.

Do đó $\vec{O A} = \frac{1}{2} \vec{C A} = \frac{1}{2} (\vec{C B} + \vec{B A})$ ⇒ B đúng.

Đáp án C: Gọi I, J lần lượt là trung điểm của AB và CD.

Ta có $\vec{O A} + \vec{O B} = 2 \vec{O I}$ và $\vec{O C} + \vec{O D} = 2 \vec{O J}$ .

Mà $\vec{O I}, \vec{O J}$ là hai vectơ đối nhau.

Do đó $2 \vec{O I} \neq 2 \vec{O J}$ .

Suy ra $\vec{O A} + \vec{O B} \neq \vec{O C} + \vec{O D}$ ⇒ C sai.

Đáp án D: Ta có OI là đường trung bình của tam giác ABD.

Suy ra $\vec{O I} = \frac{1}{2} \vec{D A}$ .

Ta có $\vec{O A} + \vec{O B} = 2 \vec{O I} = 2. \frac{1}{2} \vec{D A} = \vec{D A}$ ⇒ D đúng.

Vậy ta chọn đáp án C.

Câu 6:

Cho tam giác ABC. Gọi I là trung điểm AB. Tìm điểm M thỏa mãn hệ thức $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0}$ .

A. M là trung điểm BC;

B. M là trung điểm IC;

C. M là trung điểm IA;

D. M là điểm trên cạnh IC sao cho IM = 2MC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0} \Leftrightarrow 2 \vec{M I} + 2 \vec{M C} = \vec{0} \Leftrightarrow 2 (\vec{M I} + \vec{M C}) = \vec{0} \Leftrightarrow \vec{M I} + \vec{M C} = \vec{0}$ .

Do đó ta suy ra M là trung điểm IC.

Vậy ta chọn đáp án B.

Câu 7:

Cho hình bình hành ABCD, điểm M thỏa mãn $4 \vec{A M} = \vec{A B} + \vec{A D} + \vec{A C}$ . Xác định vị trí điểm M.

A. M là trung điểm AC;

B. Điểm M trùng với điểm C;

C. M là trung điểm AB;

D. M là trung điểm AD.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

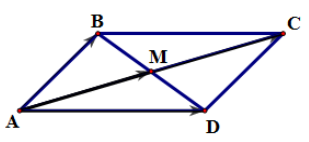
Theo quy tắc hình bình hành, ta có $\vec{A B} + \vec{A D} = \vec{A C}$ .

Ta có $4 \vec{A M} = \vec{A B} + \vec{A D} + \vec{A C}$

$\Leftrightarrow 4 \vec{A M} = 2 \vec{A C}$

$\Leftrightarrow \vec{A M} = \frac{1}{2} \vec{A C}$

Suy ra M là trung điểm AC.

Vậy ta chọn đáp án A.

Câu 8:

Cho tam giác đều ABC cạnh a. Tính độ dài $\vec{A B} + \vec{A C}$ .

A. $|\vec{A B} + \vec{A C}| = a \sqrt{3}$

B. $|\vec{A B} + \vec{A C}| = \frac{a \sqrt{3}}{2}$

C. $|\vec{A B} + \vec{A C}| = 2 a$

D. Đáp án khác

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

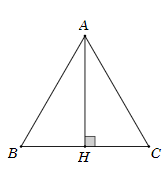
Gọi H là trung điểm BC. Ta suy ra BH = $\frac{B C}{2} = \frac{a}{2}$ .

Vì H là trung điểm BC nên ta có $\vec{A B} + \vec{A C} = 2 \vec{A H}$ .

Do đó $|\vec{A B} + \vec{A C}| = |2 \vec{A H}| = 2 A H$ .

Tam giác ABC đều có AH là đường trung tuyến.

Suy ra AH cũng là đường cao của tam giác ABC.

Tam giác ABH vuông tại H: $A H^{2} = A B^{2} - B H^{2}$ (Định lý Pytago)

$\Leftrightarrow A H^{2} = a^{2} - \frac{a^{2}}{4} = \frac{3 a^{2}}{4}$

$\Rightarrow A H = \frac{a \sqrt{3}}{2}$ .

Suy ra $|\vec{A B} + \vec{A C}| = 2 A H = 2. \frac{a \sqrt{3}}{2} = a \sqrt{3}$ .

Vậy ta chọn đáp án A.

Câu 9:

Cho tam giác ABC có điểm O thỏa mãn $|\vec{O A} + \vec{O B} - 2 \vec{O C}| = |\vec{O A} - \vec{O B}|$ . Khẳng định nào sau đây là đúng?

A. Tam giác ABC đều;

B. Tam giác ABC cân tại C;

C. Tam giác ABC vuông tại C;

D. Tam giác ABC cân tại B.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

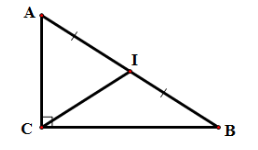
Gọi I là trung điểm AB. Ta suy ra $\vec{C A} + \vec{C B} = 2 \vec{C I}$ .

Ta có $|\vec{O A} + \vec{O B} - 2 \vec{O C}| = |\vec{O A} - \vec{O B}|$

$\Leftrightarrow |\vec{O A} - \vec{O C} + \vec{O B} - \vec{O C}| = |\vec{B A}|$

$\Leftrightarrow |\vec{C A} + \vec{C B}| = B A$

$\Leftrightarrow |2 \vec{C I}| = A B$

⇔ 2.CI = AB

$\Leftrightarrow C I = \frac{1}{2} A B$

Do đó tam giác ABC vuông tại C (đường trung tuyến trong tam giác vuông bằng một nửa cạnh huyền).

Vậy ta chọn đáp án C.

Câu 10:

Cho tam giác ABC và một điểm M tùy ý. Cho $\vec{v} = \vec{M A} + \vec{M B} - 2 \vec{M C}$ . Hãy xác định vị trí của điểm D sao cho $\vec{C D} = \vec{v}$ .

A. D là điểm thứ tư của hình bình hành ABCD;

B. D là điểm thứ tư của hình bình hành ACBD;

C. D là trọng tâm của tam giác ABC;

D. D là trực tâm của tam giác ABC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có $\vec{v} = \vec{M A} + \vec{M B} - 2 \vec{M C} = \vec{M A} - \vec{M C} + \vec{M B} - \vec{M C} = \vec{C A} + \vec{C B} = 2 \vec{C I}$ (với I là trung điểm AB).

Do đó $\vec{v}$ không phụ thuộc vào vị trí của điểm M.

Khi đó $\vec{C D} = \vec{v} = 2 \vec{C I}$ .

Suy ra I là trung điểm CD.

Vậy D là điểm thứ tư của hình bình hành ACBD.

Vậy ta chọn đáp án B.

Câu 11:

Cho tam giác ABC. Gọi M là trung điểm BC và N là trung điểm AM. Đường thẳng BN cắt AC tại P. Khi đó $\vec{A C} = x \vec{C P}$ thì giá trị của x là:

A. $- \frac{4}{3}$

B. $- \frac{2}{3}$

C. $- \frac{3}{2}$

D. $- \frac{5}{3}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

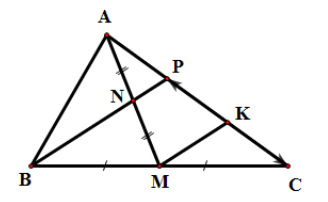
Kẻ MK // BP (K ∈ AC). Do M là trung điểm BC nên ta suy ra K là trung điểm CP (1).

Vì MK // NP, mà N là trung điểm AM nên ta suy ra P là trung điểm AK (2).

Từ (1), (2) ta suy ra AP = PK = KC.

Do đó AP = $\frac{1}{2}$ CP.

Ta có AC = AP + CP.

Suy ra AC = $\frac{3}{2}$ CP.

Vì $\vec{A C}, \vec{C P}$ ngược hướng với nhau.

Nên $\vec{A C} = - \frac{3}{2} \vec{C P}$ .

Do đó x = $- \frac{3}{2}$ .

Vậy ta chọn đáp án C.

Câu 12:

Cho tam giác OAB vuông cân tại O với OA = OB = a. Độ dài của $\vec{u} = \frac{21}{4} \vec{O A} - \frac{5}{2} \vec{O B}$ là:

A. $\frac{a \sqrt{140}}{4}$

B. $\frac{a \sqrt{321}}{4}$

C. $\frac{a \sqrt{520}}{4}$

D. $\frac{a \sqrt{541}}{4}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

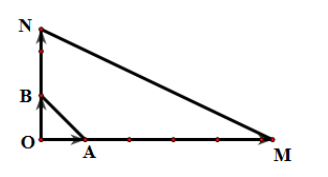
Dựng điểm M, N sao cho $\vec{O M} = \frac{21}{4} \vec{O A}$ và $\vec{O N} = \frac{5}{2} \vec{O B}$ . Khi đó ta có:

$|\vec{u}| = |\frac{21}{4} \vec{O A} - \frac{5}{2} \vec{O B}| = |\vec{O M} - \vec{O N}| = |\vec{N M}| = M N$ .

Từ dữ kiện $\vec{O M} = \frac{21}{4} \vec{O A}$ .

Ta suy ra $\vec{O M}$ cùng phương với $\vec{O A}$ .

Vì $\vec{O M}, \vec{O A}$ có cùng điểm đầu là O.

Nên giá của $\vec{O M}, \vec{O A}$ trùng nhau.

Do đó ta có OM ≡ OA.

Tương tự ta có ON ≡ OB.

Mà OA ⊥ OB (tam giác OAB vuông cân tại O).

Do đó OM ⊥ ON.

Ta có $\vec{O M} = \frac{21}{4} \vec{O A} \Leftrightarrow |\vec{O M}| = |\frac{21}{4} \vec{O A}| \Leftrightarrow O M = \frac{21}{4} O A = \frac{21 a}{4}$ .

Tương tự, ta có $\vec{O N} = \frac{5}{2} \vec{O B} \Leftrightarrow |\vec{O N}| = |\frac{5}{2} \vec{O B}| \Leftrightarrow O N = \frac{5}{2} O B = \frac{5 a}{2}$ .

Tam giác OMN vuông tại O: $M N^{2} = O M^{2} + O N^{2}$ (Định lý Pytago)

\Leftrightarrow M N^{2} = \frac{441 a^{2}}{16} + \frac{25 a^{2}}{4} = \frac{541 a^{2}}{16}

$\Rightarrow M N = \frac{a \sqrt{541}}{4}$ .

Vậy ta chọn đáp án D.

Câu 13:

Cho tam giác ABC có trọng tâm G. Biểu diễn $\vec{A G}$ theo hai vectơ $\vec{A B}, \vec{A C}$ .

A. $\vec{A G} = \frac{1}{3} (\vec{A B} + \vec{A C})$

B. $\vec{A G} = \frac{1}{6} (\vec{A B} + \vec{A C})$

C. $\vec{A G} = \frac{1}{6} (\vec{A B} - \vec{A C})$

D. $\vec{A G} = \frac{1}{3} (\vec{A B} - \vec{A C})$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

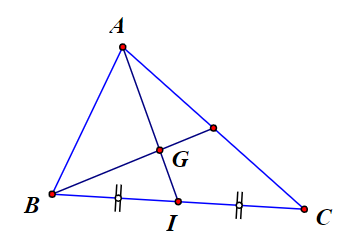
Gọi I là trung điểm BC. Ta suy ra $2 \vec{A I} = \vec{A B} + \vec{A C}$

Ta có G là trọng tâm tam giác ABC nên $A G = \frac{2}{3} A I$ .

Mà $\vec{A G}, \vec{A I}$ cùng hướng.

Do đó $\vec{A G} = \frac{2}{3} \vec{A I}$ .

Suy ra $\vec{A G} = \frac{1}{3} (\vec{A B} + \vec{A C})$ .

Vậy ta chọn đáp án A.

Câu 14:

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm AB, CD. Khi đó $\vec{A C} + \vec{B D}$ bằng

A. $\vec{M N}$

B. $2 \vec{M N}$

C. $3 \vec{M N}$

D. $- 2 \vec{M N}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

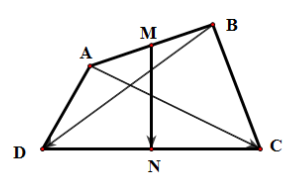
Vì M là trung điểm AB nên $\vec{M A} + \vec{M B} = \vec{0} \Leftrightarrow - (\vec{A M} + \vec{B M}) = \vec{0} \Leftrightarrow \vec{A M} + \vec{B M} = \vec{0}$ .

Vì N là trung điểm CD nên $\vec{N C} + \vec{N D} = \vec{0}$ .

Theo quy tắc ba điểm, ta có $\vec{A C} + \vec{B D} = \vec{A M} + \vec{M N} + \vec{N C} + \vec{B M} + \vec{M N} + \vec{N D}$

Suy ra $\vec{A C} + \vec{B D} = (\vec{A M} + \vec{B M}) + (\vec{N C} + \vec{N D}) + 2 \vec{M N} = \vec{0} + \vec{0} + 2 \vec{M N} = 2 \vec{M N}$

Vậy ta chọn đáp án B.

Câu 15:

Cho hình bình hành ABCD tâm O và điểm M bất kỳ. Khẳng định nào sau đây đúng?

A. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{M O}$

B. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 2 \vec{M O}$

C. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 3 \vec{M O}$

D. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

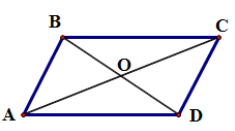
Vì O là tâm của hình bình hành ABCD nên O là trung điểm của AC và BD.

Vì O là trung điểm AC và M là điểm tùy ý nên $\vec{M A} + \vec{M C} = 2 \vec{M O}$ (1).

Vì O là trung điểm BD và M là điểm tùy ý nên $\vec{M B} + \vec{M D} = 2 \vec{M O}$ (2).

Lấy (1) + (2) vế theo vế, ta được: $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ .

Vậy ta chọn đáp án D.