20 câu hỏi trắc nghiệm thuộc 50 câu trắc nghiệm Thống kê nâng cao (P1)

Câu 1:

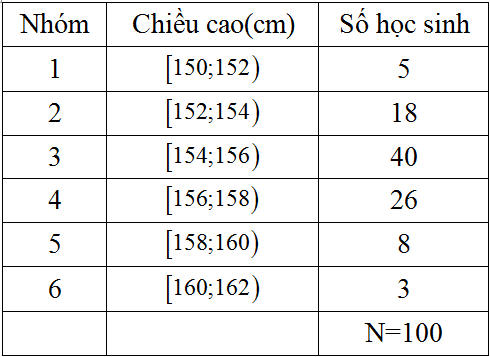
Điều tra về chiều cao của 100 học sinh khối lớp 10, ta có kết quả sau:

Giá trị đại diện của nhóm thứ 4 là:

A. 156,5

B. 157

C. 156

D. 158

Xem đáp án

Chọn B.

Giá trị đại diện của nhóm thứ 4 là: (158 + 156) : 2 = 157.

Câu 2:

Có 100 học sinh tham dự kì thi học sinh giỏi cấp thành phố môn Anh (thang điểm 20). Kết quả như sau:

Số trung vị là:

A. 15

B. 15,5

C. 16,5

D. 16

Xem đáp án

Chọn B

Ta thấy N = 100 chẵn nên số trung vị là trung bình cộng của số đứng ở vị trí thứ 50 và 51.

Giá trị đứng ở vị tri 50 là 15 và giá trị đứng ở vị trí 51 là 16

Do đó; số trung vị cần tìm là:

Câu 3:

Có 100 học sinh tham dự kì thi học sinh giỏi cấp quốc gia môn toán (thang điểm 20). Kết quả như sau:

Phương sai là:

A. $S_{x}^{2} = 3, 95$

B. $S_{x}^{2} = 3, 96$

C. ${S_{x}}^{2} = 3, 97$

D. đáp số khác

Xem đáp án

Chọn B.

Ta có:

trong đó:

Câu 4:

Cho bảng phân bố tần số- tần suất ghép lớp khi đo chiều cao (cm) của 40 học sinh nam tại một trường THPT:

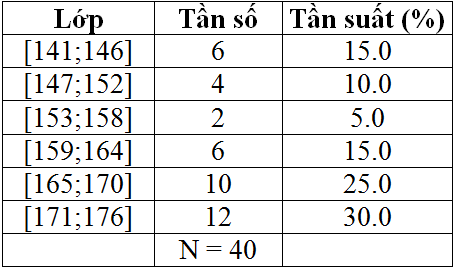
Chiều cao trung bình là:

A. 162, 4

B. 160, 4

C. 162, 3

D. 161, 4

Xem đáp án

Chọn A.

Ta có:

Câu 5:

Chiều cao của 45 cây hoa hồng (tính bằng cm) được ghi lại như sau: (lập bảng ghép lớp):

[98; 103); [103; 108); [108; 113); [113; 118); [118; 123); [123; 128); [128; 133); [133; 138); [138; 143); [143; 148].

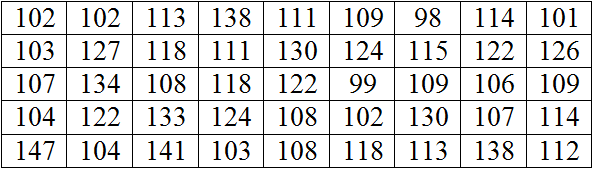
Số trung bình cộng:

A. 115,4

B. 116,4

C. 116,3

D. 166,4

Xem đáp án

Chọn B

Dựa vào bảng phân dữ liệu đề bài cho ta có bảng phân bố tần số, tần suất như sau:

Số trung bình cộng của bảng số liệu:

Câu 6:

Chiều cao của 45 cây hoa hồng (tính bằng cm) được ghi lại như sau: (lập bảng ghép lớp):

[98; 103); [103; 108); [108; 113); [113; 118); [118; 123); [123; 128); [128; 133); [133; 138); [138; 143); [143; 148].

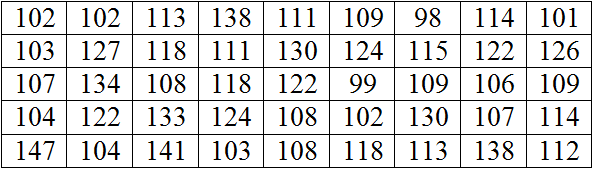
Phương sai là:

A. 155,4

B. 151, 4

C. 151, 1

D. 152,4

Xem đáp án

Chọn B

Dựa vào bảng phân dữ liệu đề bài cho ta có bảng phân bố tần số, tần suất như sau:

Phương sai của bảng số liệu.

Câu 7:

Cho bảng số liệu.

Tính số trung bình là:

A. 155,46

B. 155,12

C. 154,98

D. 154,75

Xem đáp án

Chọn A.

Để tính số trung bình ta xác định thêm cột giá trị đại diện của mỗi lớp

Trung bình cộng của bảng số liệu là:

Câu 8:

Cho bảng số liệu.

Tính độ lệch chuẩn

A. 0,78

B. 1,28

C. 2,17

D. 1,73

Xem đáp án

Chọn C.

Để tính độ lệch chuẩn thì trước hết ta tính phương sai:

trong đó:

Vậy

Nên

Câu 9:

Điều tra về số học sinh của khối lớp 10, ta được mẫu số liệu sau.

39 39 40 40 40 40 41 41 41 42 42 43 44 44 44 44 45 45

Số trung vị là:

A. 41

B. 41,5

C. 42

D. số khác

Xem đáp án

Chọn B

Do kích thước mẫu N = 18 là số chẵn nên số trung vị là trung bình cộng của 2 giá trị đứng ở vị trí thứ 9 và thứ 10

Câu 10:

Điều tra về số học sinh của khối lớp 10, ta được mẫu số liệu sau.

39 39 40 40 40 40 41 41 41 42 42 43 44 44 44 44 45 45

Số trung bình gần với số nguyên nào nhất.

A. 42

B. 41

C. 43

D. 44

Xem đáp án

Chọn A.

Để tính số trung bình ta ghi lại số liệu theo bảng tần số:

Vậy số trung bình gần với số 42 nhất.

Câu 11:

Đo chiều cao của 99 học sinh và xếp theo thứ tự tăng dần. số trung vị của dãy số liệu này là:

A. Chiều cao của học sinh thứ 50

B. Chiều cao của học sinh thứ 49

C. Chiều cao trung bình của học sinh thứ 50 và 51

D. Chiều cao trung bình của học sinh thứ 49 và thứ 50

Xem đáp án

Chọn A.

Do 99 là số lẻ nên số trung vị của dãy số liệu trên là số đứng ở vị trí chính giữa ; tức là giá trị đứng ở vị trí thứ 50.

Câu 12:

Điều tra về cân nặng của 40 con lợn, một nhà chăn nuôi đã ghi lại số liệu sau:

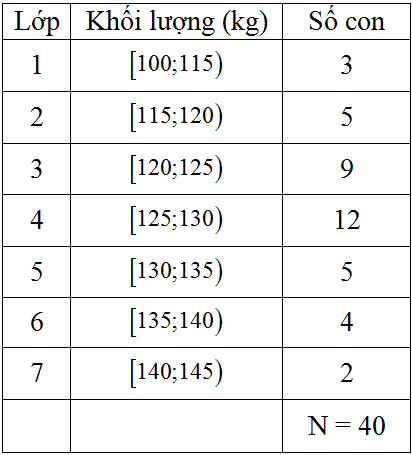
Số trung bình là:

A. 126

B. 127

C. 128

D. 129

Xem đáp án

Chọn A.

Để tính số trung bình ta xác định thêm cột giá trị đại diện vào bảng:

Lớp	Khối lượng (kg)	Tần số	Giá trị đại diện
1	[110;115)	3	107,5
2	[115;120)	5	117,5
3	[120;125)	9	122,5
4	[125;130)	12	127,5
5	[130;135)	5	132,5
6	[135;140)	4	137,5
7	[140;145)	2	142,5
		N = 40

Số trung bình cộng của dãy số liệu trên là:

$\bar{x} = \frac{107, 5.3 + 117, 5.5 + 122, 5.9 + 127, 5.12 + 132, 5.5 + 137, 5.4 + 142, 5.2}{40} = 126$

Câu 13:

Vẫn cho bảng số liệu.

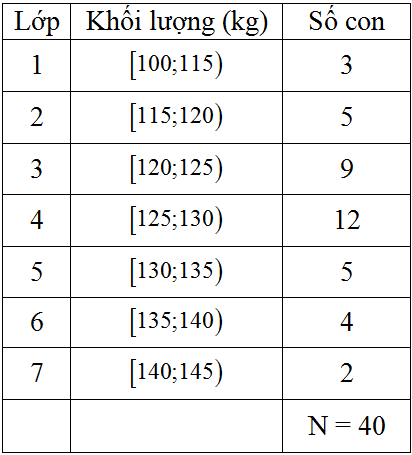
Tính phương sai:

A. 90,45

B. 70,25

C. 80,45

D. 70,15

Xem đáp án

Chọn B.

Để tính số trung bình ta xác định thêm cột giá trị đại diện vào bảng:

Lớp	Khối lượng (kg)	Tần số	Giá trị đại diện
1	[110;115)	3	107,5
2	[115;120)	5	117,5
3	[120;125)	9	122,5
4	[125;130)	12	127,5
5	[130;135)	5	132,5
6	[135;140)	4	137,5
7	[140;145)	2	142,5
		N = 40

Dựa vào bảng phân bố tần số như câu 6 ta xác định được phương sai là

$s_{x}^{2} = \bar{x^{2}} - {(\bar{x})}^{2} = \frac{1}{N} \sum_{} n_{i} . x_{i}^{2} - {(\frac{1}{N} \sum_{} n_{i} . x_{i})}^{2} = 70, 25$

Câu 14:

Kết quả học tập của hai hoc sinh A và B như sau:

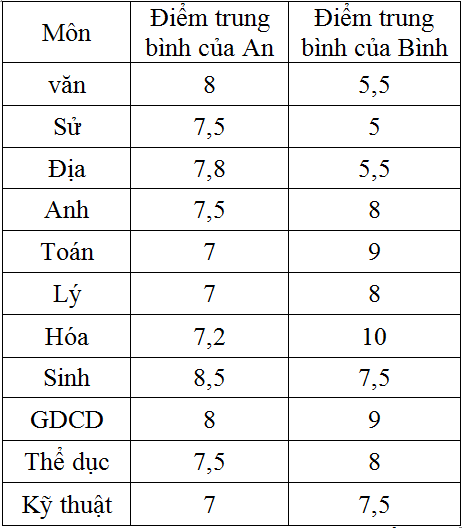
Điểm trung bình cả năm ( không tính hệ số) của học sinh An và Bình lần lượt là:

A. 7,0 và 7,5

B. 7,3 và 7,4

C. 7,5 và 7,5

D. 7,8 và 7,2

Xem đáp án

Chọn C.

+ Điểm trung bình của học sinh A:

+ Điểm trung bình của học sinh B:

Câu 15:

Cho bảng số liệu:

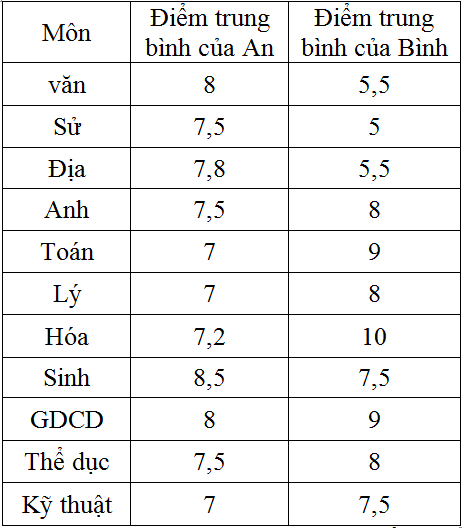
Tính phương sai và độ lệch chuẩn của An là:

A. 0,22 và 0,47

B. 0,2 và 0,41

C. 0,21 và 0, 48

D. 0,32 và 0,96

Xem đáp án

Chọn A.

Phương sai và độ lệch chuẩn của An:

Ta có và

nên

Câu 16:

Cho bảng số liệu.

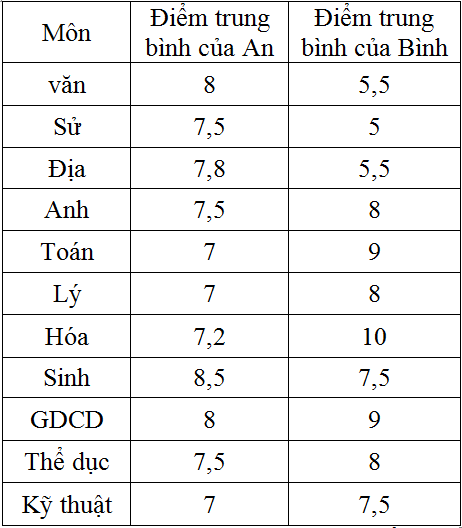
Tính phương sai và độ lệch chuẩn của Bình là:

A. 1,92 và 1,39

B. 2,34 và 1,53

C. 2,4 và 1,6

D. 1,34 và 1,53

Xem đáp án

Chọn B.

Phương sai và độ lệch chuẩn của Bình là:

Ta có $\sum_{i = 1}^{11} x_{i} = 83$ và $\sum_{i = 1}^{11} x_{i}^{2} = 652$

$s_{B}^{2} = \frac{652}{11} - {(\frac{83}{11})}^{2} \approx 2, 34 \Rightarrow s_{B} = \sqrt{2, 34} \approx 1, 53$

Câu 17:

Để được cấp chứng chỉ môn Anh trình độ A₂ của một trung tâm ngoại ngữ , học viên phải trải qua 6 lần kiểm tra trắc nghiệm , thang điểm mỗi lần kiểm tra là 100, và phải đạt điểm trung bình từ 70 điểm trở lên.Qua 5 lần thi Hoa đạt điểm trung bình là 64,5 điểm . Hỏi trong lần kiểm tra cuối cùng Hoa phải đạt ít nhất là bao nhiêu điểm để được cấp chứng chỉ?

A. 97,5

B. 92,5

C. 95,5

D. 97,8

Xem đáp án

Chọn A.

Gọi x là số điểm trong lần kiểm tra cuối mà Hoa cần đạt được để được cấp chứng chỉ.

Ta có số điểm qua 5 lần thi của Hoa là 64,5.5 = 322,5 suy ra:

$\frac{x + 322, 5}{6} \geq 70 \Leftrightarrow x \geq 70.6 - 322, 5 = 97, 5$

Câu 18:

Tiền lãi ( nghìn đồng) trong 30 ngày được khảo sát ở một quầy bánh kẹo:

Lập bảng phân bố tần số- tần suất ghép lớp: [29.5; 40.5), [40.5; 51.5), [51.5; 62.5), [62.5; 73.5), [73.5; 84.5), [84.5; 95.5]

Số trung bình cộng là:

A. 61,35

B. 63,23

C. 66,33

D. Tất cả sai

Xem đáp án

Chọn B

Ta có bảng phân bố tần số ; tần suất ghép lớn như sau:

Từ đó ta tính được số trung bình cộng là:

Câu 19:

Cho bảng số liệu như câu 18:

Tính số phương sai của bảng số liệu là:

A. 279,78

B. 282,93

C. 278,31

D. Đáp án khác

Xem đáp án

Chọn A.

Dựa vào bảng phân bố tần số; tần suất ghép lớn như câu 12 ta tính được phương sai của dãy số liệu là:

Câu 20:

Sau một tháng gieo trồng hoa hồng, người ta thu được số liệu sau về chiều cao(đơn vị:mm) của các cây hoa được trồng:

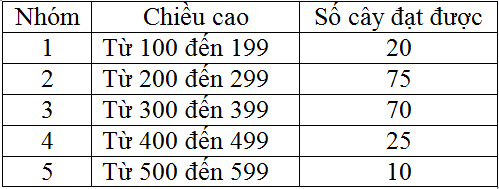
Số trung bình cộng gần nhất với giá trị nào sau đây:

A. 315

B. 390

C. 431

D. 139

Xem đáp án

Chọn A.

Từ bảng số liệu đã cho ta có bảng phân bố tần số; tần suất ghép lớn như sau:

Lớp	Tần số ( $n_{i}$ )	Tần suất ( $f_{i}$ )	Phần tử đại diện ( $c_{i}$ )	$n_{i} . c_{i}$	$n_{i} c_{i}^{2}$
[100;199]	20	10%	149,5	2990	447005
[200;299]	75	38%	249,5	18712,5	4668768,75
[300;399]	70	35%	349,5	24465	8550517,5
[400;499]	25	13%	449,5	11237,5	5051256.25
[500;599]	10	5%	549,5	5495	3019502,5
	N=200	100%		62900	21737050

Dựa vào bảng trên ta có số trung bình cộng của dãy số liệu là:

$\bar{x} = \underset{}{\sum n_{i} c_{i} = \frac{62900}{200} = 314, 5}$