Trắc nghiệm Toán 10 CTST Bài 1. Hàm số và đồ thị có đáp án (Thông hiểu)
-
1798 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta thấy trong cả bốn hệ thức trên, đại lượng x đều nhận giá trị thuộc tập số D = ℝ.
• Ở ba phương án A, B, D, ta thấy với mỗi giá trị x ∈ ℝ, ta đều xác định được một và chỉ một giá trị tương ứng y ∈ ℝ.
Do đó các hệ thức ở đáp án A, B, D đều cho ta một hàm số.
• Ở phương án C, ta thấy hệ thức đã cho không thỏa mãn định nghĩa hàm số. Cụ thể:
Với x = 1, ta có y2 = 1 + 8 = 9.
Nghĩa là, y = 3 hoặc y = –3.
Do đó tồn tại một giá trị x = 1 ∈ ℝ, ta xác định được hai giá trị tương ứng y ∈ ℝ là y = 3 hoặc y = –3.
Vì vậy hệ thức ở phương án C không cho ta một hàm số y của x.
Vậy ta chọn phương án C.
Câu 2:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Biểu thức f(x) có nghĩa khi và chỉ khi \(\left\{ \begin{array}{l}x + 1 \ge 0\\x \ne 0\end{array} \right.\).
Tức là khi \(\left\{ \begin{array}{l}x \ge - 1\\x \ne 0\end{array} \right.\).
Vì vậy tập xác định của hàm số này là D = [–1; +∞) \ {0}.
Vậy ta chọn phương án C.
Câu 3:
Tập giá trị T của hàm số \(y = \sqrt {x + 3} \).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(\sqrt {x + 3} \ge 0,\,\forall x \in D\).
Nghĩa là, y ≥ 0, ∀x ∈ D.
Vì vậy tập giá trị T của hàm số là T = [0; +∞).
Vậy ta chọn phương án C.
Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Xét hàm số \(y = f\left( x \right) = \frac{3}{x}\) trên khoảng (0; +∞).
Lấy x1, x2 tùy ý thuộc khoảng (0; +∞) sao cho x1 < x2, ta có:
f(x1) – f(x2) = \(\frac{3}{{{x_1}}} - \frac{3}{{{x_2}}} = \frac{{3{x_2} - 3{x_1}}}{{{x_1}{x_2}}} = \frac{{3\left( {{x_2} - {x_1}} \right)}}{{{x_1}{x_2}}}\).
Vì x1 < x2 nên x2 – x1 > 0 và vì x1, x2 ∈ (0; +∞) nên x1x2 > 0.
Từ đây ta suy ra \(\frac{{3\left( {{x_2} - {x_1}} \right)}}{{{x_1}{x_2}}} > 0\).
Do đó f(x1) – f(x2) > 0 hay f(x1) > f(x2).
Vì vậy hàm số đã cho nghịch biến trên khoảng (0; +∞).
Vậy ta chọn phương án A.
Câu 5:
Điểm nào sau đây thuộc đồ thị hàm số \[y = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\]?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta đặt \[f\left( x \right) = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\].
Biểu thức f(x) có nghĩa khi và chỉ khi x(3x – 4) ≠ 0.
Tức là khi x ≠ 0 và 3x – 4 ≠ 0.
Do đó x ≠ 0 và \(x \ne \frac{4}{3}\).
Vì vậy hàm số có tập xác định là \(D = \mathbb{R}\backslash \left\{ {0;\frac{4}{3}} \right\}\).
Các điểm M, P có hoành độ lần lượt là 0 và \(\frac{4}{3}\) đều không thuộc tập xác định D của hàm số đã cho.
Do đó ta loại phương án A, C.
⦁ Ta xét điểm \(N\left( {2; - \frac{3}{4}} \right)\), ta có hoành độ 2 ∈ D.
Ta có \[f\left( 2 \right) = \frac{{2.2 - 1}}{{2\left( {3.2 - 4} \right)}} = \frac{3}{4} \ne - \frac{3}{4}\].
Do đó điểm \(N\left( {2; - \frac{3}{4}} \right)\) không thuộc đồ thị hàm số \[y = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\].
Vì vậy ta loại phương án B.
⦁ Ta xét điểm \(Q\left( { - 2; - \frac{1}{4}} \right)\), ta có –2 ∈ D.
Ta có \[f\left( { - 2} \right) = \frac{{2.\left( { - 2} \right) - 1}}{{ - 2\left[ {3.\left( { - 2} \right) - 4} \right]}} = - \frac{1}{4}\].
Do đó điểm \(Q\left( { - 2; - \frac{1}{4}} \right)\) thuộc đồ thị hàm số \[y = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\].
Vậy ta chọn phương án D.
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Trường hợp 1: x ≤ 0.
Biểu thức f(x) = \(\frac{{ - 1}}{{x - 1}}\) xác định khi và chỉ khi x – 1 ≠ 0.
Nghĩa là, x ≠ 1.
Giao với điều kiện x ≤ 0, ta được x ≤ 0.
Trường hợp 2: x > 0.
Biểu thức f(x) = \(\sqrt {x + 2} \) xác định khi và chỉ khi x + 2 ≥ 0.
Nghĩa là, x ≥ –2.
Giao với điều kiện x > 0, ta được x > 0.
Vì vậy khi hợp điều kiện của trường hợp 1 và trường hợp 2, ta thu được tập xác định của hàm số là D = ℝ.
Vậy ta chọn phương án B.
Câu 7:
Hàm số y = f(x) có đồ thị như hình vẽ bên.
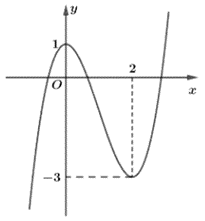
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Từ đồ thị, ta thấy hàm số xác định trên ℝ.
+) Trên khoảng (–∞; 0), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (–∞; 0).
+) Trên khoảng (0; 2), đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (0; 2).
+) Trên khoảng (2; +∞), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (2; +∞).
Phương án A sai vì hàm số đồng biến trên (–∞; 0) và (2; 3); nhưng nghịch biến trên khoảng (0; 2).
Phương án B sai vì hàm số đồng biến trên (–∞; 0) nhưng nghịch biến trên khoảng (0; 1).
Phương án C đúng.
Phương án D sai vì hàm số đồng biến trên (–3; 0) và (2; +∞) nhưng nghịch biến trên khoảng (0; 2).
Vậy ta chọn phương án C.
Câu 8:
Xét tính đồng biến, nghịch biến của hàm số \(y = \sqrt[3]{x} + 3\).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Xét hàm số \(y = f\left( x \right) = \sqrt[3]{x} + 3\).
Tập xác định của hàm số này là D = ℝ.
Lấy x1, x2 tùy ý thuộc ℝ sao cho x1 < x2, ta có: x1 < x2.
Suy ra \(\sqrt[3]{{{x_1}}} < \sqrt[3]{{{x_2}}}\).
Khi đó ta có \(\sqrt[3]{{{x_1}}} + 3 < \sqrt[3]{{{x_2}}} + 3\).
Do đó f(x1) < f(x2).
Vì vậy hàm số đã cho đồng biến (tăng) trên ℝ.
Vậy ta chọn phương án A.
