10 câu hỏi trắc nghiệm thuộc Dạng 2: Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn có đáp án

Câu 1:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} 2 x + 3 y - 15 < 0 \\ x + y > 0 \end{cases}$ chứa điểm nào trong các điểm sau đây ?

A. (1; 15);

B. (7; 8);

C. (9; 11);

D. (1; 2).

Xem đáp án

Đáp án đúng là: D

Xét điểm (1; 2) và hệ $\{\begin{cases} 2 x + 3 y - 15 < 0 \\ x + y > 0 \end{cases}$ ta có:

2.1 + 3.2 – 15 = –7 < 0

1 + 2 = 3 > 0

Do đó, điểm (1; 2) nằm trong miền nghiệm của hệ bất phương trình $\{\begin{cases} 2 x + 3 y - 15 < 0 \\ x + y > 0 \end{cases}$ .

Câu 2:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} 2 x - y - 1 > 0 \\ x + y < 0 \end{cases}$ là phần giao của các nửa mặt phẳng nào sau đây ?

A. Nửa mặt phẳng không kể bờ 2x – y – 1 = 0 không chứa điểm (0; 0) và nửa mặt phẳng không kể bờ x + y = 0 không chứa điểm (1; 1);

B. Nửa mặt phẳng có kể bờ 2x – y – 1 = 0 không chứa điểm (0; 0) và nửa mặt phẳng không kể bờ x + y = 0 không chứa điểm (1; 1);

C. Nửa mặt phẳng không kể bờ 2x – y – 1 = 0 không chứa điểm (0; 0) và nửa mặt phẳng có kể bờ x + y = 0 không chứa điểm (1; 1);

D. Nửa mặt phẳng không kể bờ 2x – y – 1 = 0 chứa điểm (0; 0) và nửa mặt phẳng không kể bờ x + y = 0 không chứa điểm (1; 1).

Xem đáp án

Đáp án đúng là: A

Xét hệ bất phương trình $\{\begin{cases} 2 x - y - 1 > 0 \\ x + y < 0 \end{cases}$ có:

Bất phương trình 2x – y – 1 > 0:

Điểm (0; 0) không nằm trên đường thẳng 2x – y – 1 = 0 và 2.0 – 0 – 1 < 0 nên miền nghiệm của bất phương trình 2x – y – 1 > 0 là nửa mặt phẳng không kể bờ 2x – y – 1 = 0 không chứa điểm (0; 0).

Bất phương trình x + y < 0:

Điểm (1; 1) không nằm trên đường thẳng x + y = 0 và 1 + 1 > 0 nên miền nghiệm của bất phương trình x + y < 0 là nửa mặt phẳng không kể bờ x + y = 0 không chứa điểm (1; 1).

Vậy miền nghiệm của hệ bất phương trình $\{\begin{cases} 2 x - y - 1 > 0 \\ x + y < 0 \end{cases}$ là phần giao của nửa mặt phẳng không kể bờ 2x – y – 1 = 0 không chứa điểm (0; 0) và nửa mặt phẳng không kể bờ x + y = 0 không chứa điểm (1; 1)

Câu 3:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} 2 x - 3 y + 7 > 0 \\ 2 x - y + 5 < 0 \end{cases}$ là phần giao của:

A. Nửa mặt phẳng không kể bờ 2x – 3y + 7 = 0 không chứa điểm (0; 0) và nửa mặt phẳng không kể bờ 2x – y + 5 = 0 không chứa điểm (0; 0);

B. Nửa mặt phẳng không kể bờ 2x – 3y + 7 = 0 chứa điểm (0; 0) và nửa mặt phẳng không kể bờ 2x – y + 5 = 0 không chứa điểm (0; 0);

C. Nửa mặt phẳng có kể bờ 2x – 3y + 7 = 0 chứa điểm (0; 0) và nửa mặt phẳng không kể bờ 2x – y + 5 = 0 không chứa điểm (0; 0);

D. Nửa mặt phẳng không kể bờ 2x – 3y + 7 = 0 chứa điểm (0; 0) và nửa mặt phẳng không kể bờ 2x – y + 5 = 0 chứa điểm (0; 0).

Xem đáp án

Đáp án đúng là: B

Xét bất phương trình 2x – 3y + 7 > 0 ta có:

Điểm (0; 0) không nằm trên đường thẳng 2x – 3y + 7 = 0 và 2.0 – 3.0 + 7 = 7 > 0 nên miền nghiệm của bất phương trình 2x – 3y + 7 > 0 là nửa mặt phẳng không kể bờ 2x – 3y + 7 = 0 chứa điểm (0; 0).

Xét bất phương trình 2x – y + 5 < 0 ta có:

Điểm (0; 0) không nằm trên đường thẳng 2x – y + 5 = 0 và 2.0 – 0 + 5 = 5 > 0 nên

nên miền nghiệm của bất phương trình 2x – y + 5 < 0 là nửa mặt phẳng không kể bờ 2x – y + 5 = 0 không chứa điểm (0; 0).

Vậy miền nghiệm của hệ bất phương trình $\{\begin{cases} 2 x - 3 y + 7 > 0 \\ 2 x - y + 5 < 0 \end{cases}$ là phần giao của nửa mặt phẳng không kể bờ 2x – 3y + 7 = 0 chứa điểm (0; 0) và nửa mặt phẳng không kể bờ 2x – y + 5 = 0 không chứa điểm (0; 0)

Câu 4:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} 5 x - 3 y + 2 \leq 0 \\ x - 2 \geq 0 \\ y + 5 < 0 \end{cases}$ là phần giao của:

A. Nửa mặt phẳng có kể bờ 5x – 3y + 2 = 0 chứa điểm (0; 0); nửa mặt phẳng có kể bờ x – 2 = 0 chứa điểm (1; 0); nửa mặt phẳng không kể bờ y + 5 = 0 chứa điểm (–6; 0);

B. Nửa mặt phẳng có kể bờ 5x – 3y + 2 = 0 không chứa điểm (0; 0); nửa mặt phẳng có kể bờ x – 2 = 0 chứa điểm (1; 0); nửa mặt phẳng không kể bờ y + 5 = 0 chứa điểm (–6; 0);

C. Nửa mặt phẳng có kể bờ 5x – 3y + 2 = 0 không chứa điểm (0; 0); nửa mặt phẳng có kể bờ x – 2 = 0 không chứa điểm (1; 0); nửa mặt phẳng không kể bờ y + 5 = 0 không chứa điểm (–6; 0);

D. Nửa mặt phẳng không kể bờ 5x – 3y + 2 = 0 chứa điểm (0; 0); nửa mặt phẳng có kể bờ x – 2 = 0 chứa điểm (1; 0); nửa mặt phẳng không kể bờ y + 5 = 0 chứa điểm (–6; 0).

Xem đáp án

Đáp án đúng là: C

Xét bất phương trình 5x – 2y + 2 ≤ 0 ta có:

Điểm (0; 0) không nằm trên đường thẳng 5x – 2y + 2 = 0 và 5.0 – 2.0 + 2 = 2 > 0 nên miền nghiệm của bất phương trình 5x – 2y + 2 ≤ 0 là nửa mặt phẳng có kể bờ 5x – 3y + 2 = 0 không chứa điểm (0; 0).

Xét bất phương trình x – 2 ≥ 0 ta có:

Điểm (1; 0) không nằm trên đường thẳng x – 2 = 0 và 1 – 2 = –1 < 0 nên miền nghiệm của bất phương trình x – 2 ≥ 0 là nửa mặt phẳng có kể bờ x – 2 = 0 không chứa điểm (1; 0).

Xét bất phương trình y + 5 < 0 ta có:

Điểm (–6; 0) không nằm trên đường thẳng y + 5 = 0 và 0 + 5 = 5 > 0 nên miền nghiệm của bất phương trình y + 5 < 0 là nửa mặt phẳng không kể bờ y + 5 = 0, không chứa điểm (–6; 0).

Vậy miền nghiệm của hệ bất phương trình $\{\begin{cases} 5 x - 3 y + 2 \leq 0 \\ x - 2 \geq 0 \\ y + 5 < 0 \end{cases}$ là phần giao của nửa mặt phẳng có kể bờ 5x – 3y + 2 = 0 không chứa điểm (0; 0); nửa mặt phẳng có kể bờ x – 2 = 0 không chứa điểm (1; 0); nửa mặt phẳng không kể bờ y + 5 = 0 không chứa điểm (–6; 0).

Câu 5:

Phần giao của nửa mặt phẳng có kể bờ x + 2y – 3 = 0 chứa điểm (0; 0) và nửa mặt phẳng không kể bờ x – 3 = 0 không chứa điểm (0; 0) là miền nghiệm của hệ bất phương trình:

A. $\{\begin{cases} x - 2 y - 3 < 0 \\ x - 3 > 0 \end{cases}$

B. $\{\begin{cases} x + 2 y - 3 < 0 \\ x - 3 > 0 \end{cases}$

C. $\{\begin{cases} x + 2 y - 3 \leq 0 \\ x - 3 > 0 \end{cases}$

D. $\{\begin{cases} x + 2 y - 3 \leq 0 \\ x - 3 \geq 0 \end{cases}$

Xem đáp án

Đáp án đúng: C

Xét hệ $\{\begin{cases} x + 2 y - 3 \leq 0 \\ x - 3 > 0 \end{cases}$ có:

Bất phương trình x + 2y – 3 ≤ 0 có:

Điểm (0; 0) không nằm trên đường thẳng x + 2y – 3 = 0 và 0 + 2.0 – 3 < 0 nên miền nghiệm của bất phương trình x + 2y – 3 ≤ 0 là nửa mặt phẳng có kể bờ x + 2y – 3 = 0 chứa điểm (0; 0).

Bất phương trình x – 3 > 0 có:

Điểm (0; 0) không nằm trên đường thẳng x – 3 = 0 và 0 – 3 = –3 < 0 nên miền nghiệm của bất phương trình x – 3 > 0 là nửa mặt phẳng không kể bờ x – 3 = 0 không chứa điểm (0; 0).

Vậy phần giao của nửa mặt phẳng có kể bờ x + 2y – 3 = 0 chứa điểm (0; 0) và nửa mặt phẳng không kể bờ x – 3 = 0 không chứa điểm (0; 0) là miền nghiệm của hệ bất phương trình: $\{\begin{cases} x + 2 y - 3 \leq 0 \\ x - 3 > 0 \end{cases}$ .

Câu 6:

Phần giao của nửa mặt phẳng có kể bờ 2x – 3 = 0 chứa điểm (0; 0) và nửa mặt phẳng có kể bờ y – 2 = 0 chứa điểm (0; 0) là miền nghiệm của hệ bất phương trình:

A. $\{\begin{cases} 2 x - 3 \leq 0 \\ y - 2 \leq 0 \end{cases}$

B $\{\begin{cases} 2 x - 3 \leq 0 \\ y - 2 > 0 \end{cases}$

C. $\{\begin{cases} 2 x - 3 > 0 \\ y - 2 \leq 0 \end{cases}$

D. $\{\begin{cases} 2 x - 3 > 0 \\ y - 2 > 0 \end{cases}$

Xem đáp án

Đáp án đúng là: A

Xét hệ $\{\begin{cases} 2 x - 3 \leq 0 \\ y - 2 \leq 0 \end{cases}$ có:

Bất phương trình 2x – 3 ≤ 0 có:

Điểm (0; 0) không nằm trên đường thẳng 2x – 3 = 0 và 2.0 – 3 = –3 < 0 nên miền nghiệm của bất phương trình 2x – 3 ≤ 0 là nửa mặt phẳng có kể bờ 2x – 3 = 0 chứa điểm (0; 0).

Bất phương trình y – 2 ≤ 0 có:

Điểm (0; 0) không nằm trên đường thẳng y – 2 = 0 và 0 – 2 = –2 < 0 nên miền nghiệm của bất phương trình y – 2 ≤ 0 là nửa mặt phẳng có kể bờ y – 2 = 0 chứa điểm (0; 0).

Vậy phần giao của nửa mặt phẳng có kể bờ 2x – 3 = 0 chứa điểm (0; 0) và nửa mặt phẳng có kể bờ y – 2 = 0 chứa điểm (0; 0) là miền nghiệm của hệ bất phương trình: $\{\begin{cases} 2 x - 3 \leq 0 \\ y - 2 \leq 0 \end{cases}$ .

Câu 7:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} x - 3 y - 1 \leq 0 \\ x - 5 \geq 0 \end{cases}$ là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?

A.

Miền nghiệm của hệ bất phương trình x - 3y - 1 < = 0 (ảnh 2)

B.

Miền nghiệm của hệ bất phương trình x - 3y - 1 < = 0 (ảnh 3)

C.

Miền nghiệm của hệ bất phương trình x - 3y - 1 < = 0 (ảnh 4)

D.

Miền nghiệm của hệ bất phương trình x - 3y - 1 < = 0 (ảnh 5)

Xem đáp án

Đáp án đúng là: A

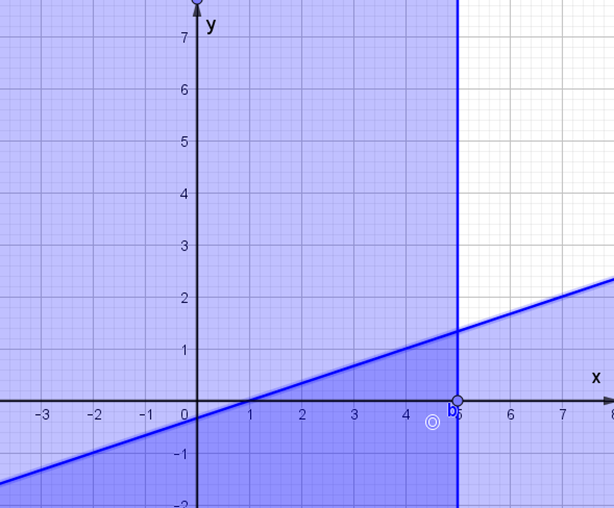
Bất phương trình x – 3y – 1 ≤ 0 có:

Điểm (0; 0) không nằm trên đường thẳng x – 3y – 1 = 0 và 0 – 3.0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – 3y – 1 ≤ 0 là nửa mặt phẳng có kể bờ x – 3y – 1 = 0 chứa điểm (0; 0).

Bất phương trình x – 5 ≥ 0 có:

Điểm (0; 0) không nằm trên đường thẳng x – 5 = 0 và 0 – 5 = –5 < 0 nên miền nghiệm của bất phương trình x – 5 ≥ 0 là nửa mặt phẳng có kể bờ x – 5 = 0 không chứa điểm (0; 0).

Miền màu trắng trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình $\{\begin{cases} x - 3 y - 1 \leq 0 \\ x - 5 \geq 0 \end{cases}$ .

Miền nghiệm của hệ bất phương trình x - 3y - 1 < = 0 (ảnh 1)

Câu 8:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} x - y + 2 > 0 \\ y + 2 > 0 \end{cases}$ là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?

A.

Miền nghiệm của hệ bất phương trình x - y + 2 > 0 (ảnh 2)

B.

Miền nghiệm của hệ bất phương trình x - y + 2 > 0 (ảnh 3)

C.

Miền nghiệm của hệ bất phương trình x - y + 2 > 0 (ảnh 4)

Miền nghiệm của hệ bất phương trình x - y + 2 > 0 (ảnh 5)

D.

Miền nghiệm của hệ bất phương trình x - y + 2 > 0 (ảnh 6)

Xem đáp án

Đáp án đúng là: D

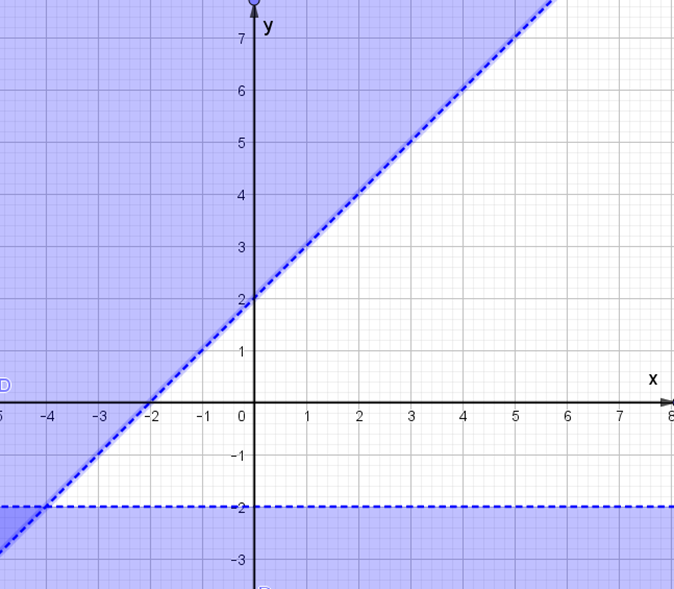
Bất phương trình x – y + 2 > 0 có:

Điểm (0; 0) không nằm trên đường thẳng x – y + 2 = 0 và 0 – 0 + 2 = 2 > 0 nên miền nghiệm của bất phương trình x – y + 2 > 0 là nửa mặt phẳng không kể bờ x – y + 2 = 0 chứa điểm (0; 0).

Bất phương trình y + 2 > 0 có:

Điểm (0; 0) không nằm trên đường thẳng y + 2 = 0 và 0 + 2 = 2 > 0 nên miền nghiệm của bất phương trình y + 2 > 0 là nửa mặt phẳng không kể bờ y + 2 = 0 chứa điểm (0; 0).

Miền màu trắng trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình $\{\begin{cases} x - y + 2 > 0 \\ y + 2 > 0 \end{cases}$ .

Miền nghiệm của hệ bất phương trình x - y + 2 > 0 (ảnh 1)

Câu 9:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} x + y \leq 8 \\ 20 x + 30 y \leq 180 \end{cases}$ là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?

A.

Miền nghiệm của hệ bất phương trình x + y < = 8 (ảnh 2)

B.

Miền nghiệm của hệ bất phương trình x + y < = 8 (ảnh 3)

C.

Miền nghiệm của hệ bất phương trình x + y < = 8 (ảnh 4)

D.

Miền nghiệm của hệ bất phương trình x + y < = 8 (ảnh 5)

Xem đáp án

Đáp án đúng là: B

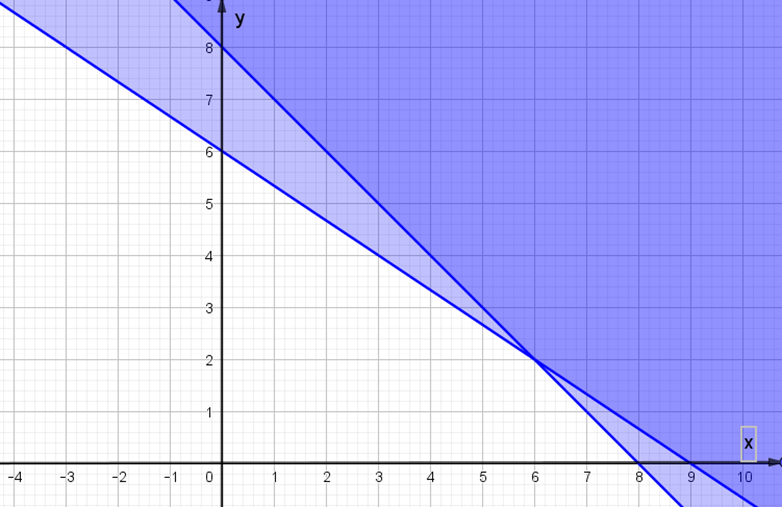
Bất phương trình x + y ≤ 8 hay x + y – 8 ≤ 0 có: Điểm (0; 0) không nằm trên đường thẳng x + y – 8 = 0 và 0 + 0 – 8 = –8 < 0 nên miền nghiệm của bất phương trình x + y ≤ 8 là nửa mặt phẳng có kể bờ x + y – 8 = 0 và chứa điểm (0; 0).

Bất phương trình 20x + 30y ≤ 180 hay 20x + 30y – 180 ≤ 0 có: Điểm (0; 0) không nằm trên đường thẳng 20x + 30y – 180 = 0 và 20.0 + 30.0 – 180 = –180 < 0 nên miền nghiệm của bất phương trình 20x + 30y ≤ 180 là nửa mặt phẳng có kể bờ 20x + 30y – 180 = 0 và chứa điểm (0; 0).

Miền màu trắng trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình $\{\begin{cases} x + y \leq 8 \\ 20 x + 30 y \leq 180 \end{cases}$ .

Miền nghiệm của hệ bất phương trình x + y < = 8 (ảnh 1)

Câu 10:

Miền nghiệm của hệ bất phương trình $\{\begin{cases} x \leq 0 \\ y \leq 0 \end{cases}$ là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?

A.

Miền nghiệm của hệ bất phương trình x < = 0; y < = 0 (ảnh 2)

B.

Miền nghiệm của hệ bất phương trình x < = 0; y < = 0 (ảnh 3)

C.

Miền nghiệm của hệ bất phương trình x < = 0; y < = 0 (ảnh 4)

D.

Miền nghiệm của hệ bất phương trình x < = 0; y < = 0 (ảnh 5)

Xem đáp án

Đáp án đúng là: C

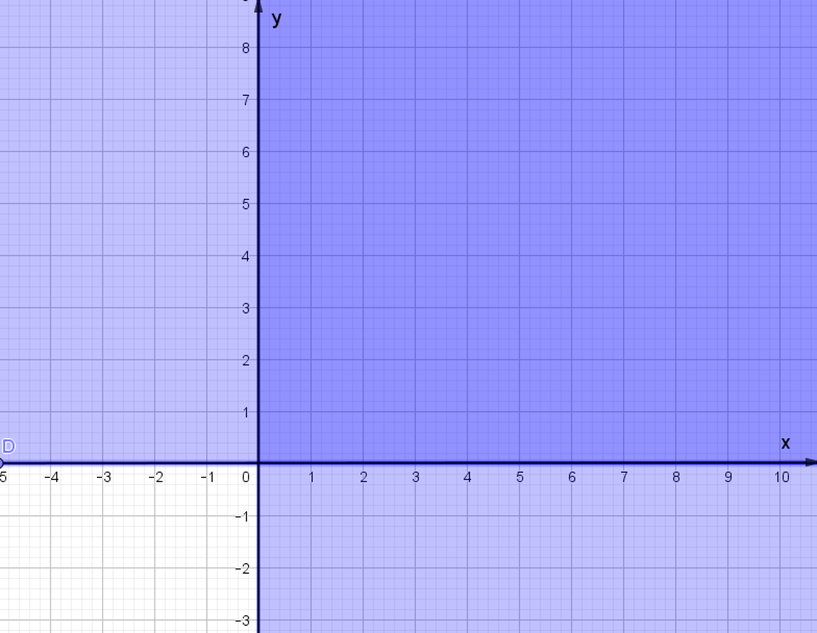
Bất phương trình x ≤ 0 có: Điểm (1; 0) không nằm trên đường thẳng x = 0 và 1 > 0 nên miền nghiệm của bất phương trình x ≤ 0 là nửa mặt phẳng có kể bờ x = 0 và không chứa điểm (1; 0).

Bất phương trình y ≤ 0 có: Điểm (0; 1) không nằm trên đường thẳng y = 0 và 1 > 0 nên miền nghiệm của bất phương trình y ≤ 0 là nửa mặt phẳng có kể bờ y = 0 và không chứa điểm (0; 1).

Miền màu trắng trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình $\{\begin{cases} x \leq 0 \\ y \leq 0 \end{cases}$ .