10 câu hỏi trắc nghiệm thuộc Dạng 2: So sánh hai mẫu số liệu tương đồng và xem xét mẫu nào ổn định hơn có đáp án

Câu 1:

Hai huyện A và B phát động phong trào hiến máu trong 7 ngày. Số lượng người đến hiến máu trong 7 ngày của 2 huyện được thống kê trong bảng dưới đây:

Ngày

Huyện

1

2

3

4

5

6

7

Huyện A

50

42

45

55

34

60

47

Huyện B

40

53

44

62

32

55

40

Sử dụng kiến thức về khoảng biến thiên và khoảng tứ phân vị, xác định xem số lượng người tham gia của huyện nào ổn định hơn?

A. Huyện A;

B. Huyện B;

C. Số người tham gia ở hai huyện đều ổn định như nhau;

D. Số người tham gia ở hai huyện đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

- Sắp xếp số lượng người tham gia hiến máu của huyện A trong 7 ngày theo thứ tự không giảm ta có:

34; 42; 45; 47; 50; 55; 60.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 34.

+ Giá trị lớn nhất của mẫu số liệu trên là 60.

Suy ra khoảng biến thiên R_A = 60 – 34 = 26.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 34; 42; 45.

Do đó Q_1A = 42.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 50; 55; 60.

Do đó Q_3A = 55.

Suy ra khoảng tứ phân vị ∆_QA = Q_3A – Q_1A = 55 – 42 = 13.

- Sắp xếp số lượng người tham gia hiến máu của huyện B trong 7 ngày theo thứ tự không giảm ta có:

32; 40; 40; 44; 53; 55; 62.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 32.

+ Giá trị lớn nhất của mẫu số liệu trên là 62.

Suy ra khoảng biến thiên R_B = 62 – 32 = 30.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 32; 40; 40.

Do đó Q_1B = 40.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 53; 55; 62.

Do đó Q_3B = 55.

Suy ra khoảng tứ phân vị ∆_QB = Q_3B – Q_1B = 55 – 40 = 15.

Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số lượng người tham gia hiến máu của huyện A bé hơn huyện B nên số lượng người tham gia của huyện A ổn định hơn.

Câu 2:

Hai huyện A và B phát động phong trào hiến máu trong 7 ngày. Số lượng người đến hiến máu trong 7 ngày của 2 huyện được thống kê trong bảng dưới đây:

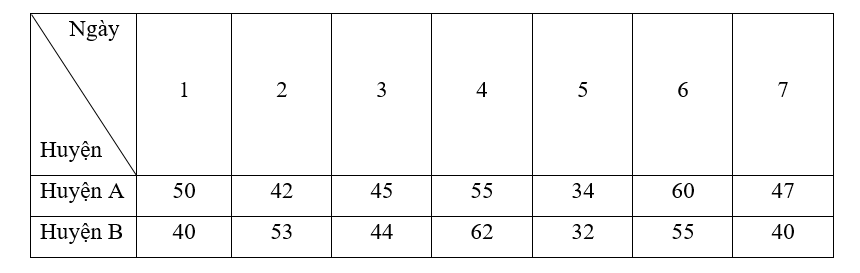
Hai huyện A và B phát động phong trào hiến máu trong 7 ngày. Số lượng người đến (ảnh 1)

Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem số lượng người tham gia của huyện nào ổn định hơn?

A. Huyện A;

B. Huyện B;

C. Số người tham gia ở hai huyện đều ổn định như nhau;

D. Số người tham gia ở hai huyện đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

- Số trung bình lượng người tham gia hiến máu trong 7 ngày của huyện A là:

$\bar{x_{A}} = \frac{50 + 42 + 45 + 55 + 34 + 60 + 47}{7} \approx 47, 57$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

= $\frac{1}{7}$ [(50 – 47,57)² + (42 – 47,57)² + (45 – 47,57)² + (55 – 47,57)² + (34 – 47,57)² + (60 – 47,57)² + (47 – 47,57)²] ≈ 62,53.

Do đó phương sai của mẫu số liệu trên là 62,53.

Độ lệch chuẩn của mẫu số liệu trên là S_A = $\sqrt{S_{A}^{2}}$ = $\sqrt{62, 53}$ ≈ 7,91.

- Số trung bình lượng người tham gia hiến máu trong 7 ngày của huyện B là:

${\bar{x}}_{B} = \frac{40 + 53 + 44 + 62 + 32 + 55 + 40}{7} \approx 46, 57$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

= $\frac{1}{7}$ [(40 – 46,57)² + (53 – 46,57)² + (44 – 46,57)² + (62 – 46,57)² + (32 – 46,57)² + (55 – 46,57)² + (40 – 46,57)²] ≈ 93,67.

Do đó phương sai của mẫu số liệu trên là 93,67.

Độ lệch chuẩn của mẫu số liệu trên là S_B = $\sqrt{S_{B}^{2}}$ = $\sqrt{93, 67}$ ≈ 9,68.

Ta thấy phương sai và độ lệch chuẩn trong số lượng người tham gia hiến máu của huyện A bé hơn huyện B nên số lượng người tham gia của huyện A ổn định hơn.

Câu 3:

Số giờ sử dụng Internet của hai bạn Nhung và Ngân trong 5 ngày được thống kê trong bảng dưới đây:

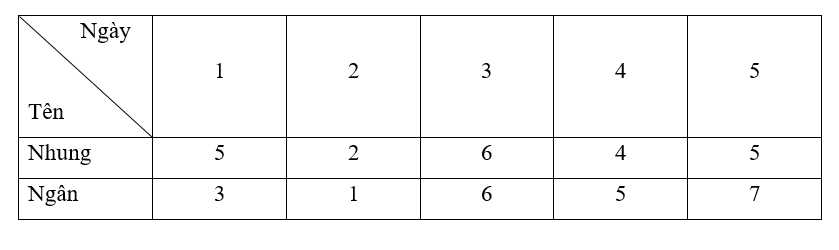
Số giờ sử dụng Internet của hai bạn Nhung và Ngân trong 5 ngày được thống kê (ảnh 1)

Sử dụng kiến thức về khoảng biến thiên và khoảng tứ phân vị, xác định xem số giờ sử dụng Internet của bạn nào ổn định hơn?

A. Ngân;

B. Nhung;

C. Số giờ sử dụng Internet của hai bạn đều ổn định như nhau;

D. Số giờ sử dụng Internet của hai bạn đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

- Sắp xếp số giờ sử dụng Internet của bạn Nhung theo thứ tự không giảm ta có:

2; 4; 5; 5; 6.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 2

+ Giá trị lớn nhất của mẫu số liệu trên là 6

Suy ra khoảng biến thiên R₁ = 6 – 2 = 4.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 2; 4.

Do đó Q₁ = $\frac{2 + 4}{2} = 3$

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 5; 6.

Do đó Q₃ = $\frac{5 + 6}{2} = 5, 5$

Suy ra khoảng tứ phân vị ∆_Q1 = Q₃ – Q₁ = 5,5 – 3 = 2,5.

- Sắp xếp số giờ sử dụng Internet của bạn Ngân theo thứ tự không giảm ta có:

1; 3; 5; 6; 7.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 1

+ Giá trị lớn nhất của mẫu số liệu trên là 7

Suy ra khoảng biến thiên R₂ = 7 – 1 = 6.

Do đó của mẫu số liệu trên là 6.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 1; 3.

Do đó Q_1' = $\frac{1 + 3}{2} = 2$

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 6; 7.

Do đó Q_3' = $\frac{6 + 7}{2} = 6, 5 .$

Suy ra khoảng tứ phân vị ∆_Q2 = Q_3' – Q_1' = 6,5 – 2 = 4,5

Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số giờ sử dụng Internet của bạn Nhung bé hơn Ngân nên số giờ sử dụng Internet của bạn Nhung ổn định hơn.

Câu 4:

Số giờ sử dụng Internet của hai bạn Nhung và Ngân trong 5 ngày được thống kê trong bảng dưới đây:

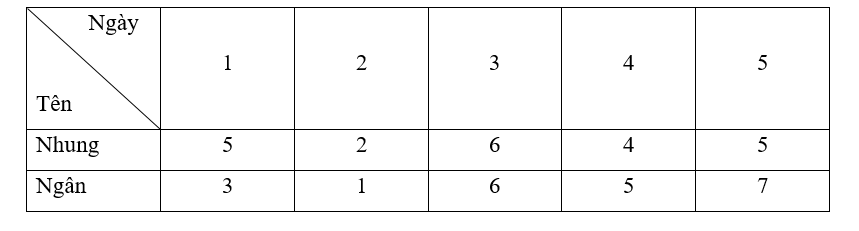
Số giờ sử dụng Internet của hai bạn Nhung và Ngân trong 5 ngày được thống kê trong (ảnh 1)

Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem số giờ sử dụng Internet của bạn nào ổn định hơn?

A. Ngân;

B. Nhung;

C. Số giờ sử dụng Internet của hai bạn đều ổn định như nhau;

D. Số giờ sử dụng Internet của hai bạn đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

- Số giờ trung bình sử dụng Internet của bạn Nhung là:

${\bar{x}}_{1} = \frac{5 + 2 + 6 + 4 + 5}{5} = 4, 4$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{2}^{2}$ = $\frac{1}{5}$ [(5 – 4,4)² + (2 – 4,4)² + (6 – 4,4)² + (4 – 4,4)² + (5 – 4,4)²] = 1,84.

Do đó phương sai của mẫu số liệu trên là 1,84.

Độ lệch chuẩn của mẫu số liệu trên là S₁ = $\sqrt{S_{1}^{2}}$ = $\sqrt{1, 84}$ ≈ 1,36.

- Số giờ trung bình sử dụng Internet của bạn Ngân là:

${\bar{x}}_{2} = \frac{3 + 1 + 6 + 5 + 7}{5} = 4, 4$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{2}^{2}$ = $\frac{1}{5}$ [(3 – 4,4)² + (1 – 4,4)² + (6 – 4,4)² + (5 – 4,4)² + (7 – 4,4)²] = 4,64.

Do đó phương sai của mẫu số liệu trên là 4,64.

Độ lệch chuẩn của mẫu số liệu trên là S₂ = $\sqrt{S_{2}^{2}} = \sqrt{4, 64}$ = ≈ 2,15.

Ta thấy phương sai và độ lệch chuẩn trong số giờ sử dụng Internet của bạn Nhung bé hơn Ngân nên số giờ sử dụng Internet của bạn Nhung ổn định hơn.

Câu 5:

Số lượng bệnh nhân khỏi bệnh của hai bệnh viện A và B trong 6 ngày được thống kê trong bảng dưới đây:

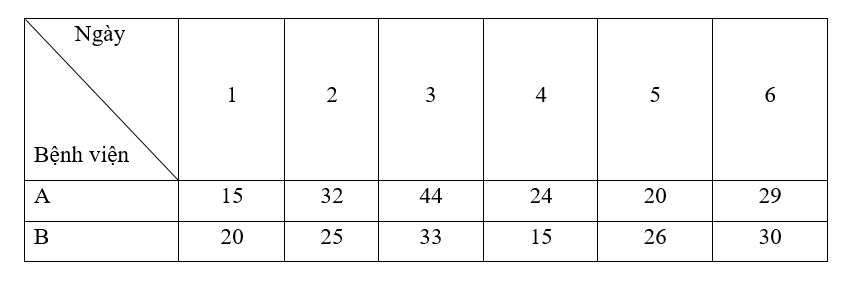
Số lượng bệnh nhân khỏi bệnh của hai bệnh viện A và B trong 6 ngày được (ảnh 1)

Sử dụng kiến thức về khoảng biến thiên và khoảng tứ phân vị, xác định xem số lượng bệnh nhân khỏi bệnh của bệnh viện nào ổn định hơn?

A. Bệnh viện A;

B. Bệnh viện B;

C. Số lượng bệnh nhân khỏi bệnh của cả hai bệnh viện đều ổn định như nhau;

D. Số lượng bệnh nhân khỏi bệnh của cả hai bệnh viện đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

- Sắp xếp số lượng bệnh nhân khỏi bệnh của bệnh viện A theo thứ tự không giảm ta có:

15; 20; 24; 29; 32; 44.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 15

+ Giá trị lớn nhất của mẫu số liệu trên là 44

Suy ra khoảng biến thiên R_A = 44 – 15 = 29.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 15; 20; 24.

Do đó Q_1A = 20.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 29; 32; 44.

Do đó Q_3A = 32.

Suy ra khoảng tứ phân vị ∆_QA = Q_3A – Q_1A = 32 – 20 = 12.

- Sắp xếp số lượng bệnh nhân khỏi bệnh của bệnh viện B theo thứ tự không giảm ta có:

15; 20; 25; 26; 30; 33.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 15

+ Giá trị lớn nhất của mẫu số liệu trên là 33

Suy ra khoảng biến thiên R_B = 33 – 15 = 18.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 15; 20; 25.

Do đó Q_1B = 20.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 26; 30; 33.

Do đó Q_3B = 30.

Suy ra ∆_QB = Q_3B – Q_1B = 30 – 20 = 10.

Do đó khoảng tứ phân vị của mẫu số liệu trên là 10.

Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số lượng bệnh nhân khỏi bệnh của bệnh viện B bé hơn bệnh viện A nên số lượng bệnh nhân khỏi bệnh của bệnh viện B ổn định hơn.

Câu 6:

Số lượng bệnh nhân khỏi bệnh của hai bệnh viện A và B trong 6 ngày được thống kê trong bảng dưới đây:

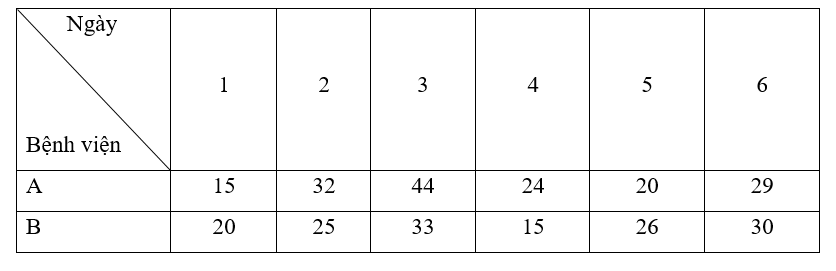
Số lượng bệnh nhân khỏi bệnh của hai bệnh viện A và B trong 6 ngày được thống kê (ảnh 1)

Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem số lượng bệnh nhân khỏi bệnh của bệnh viện nào ổn định hơn?

A. Bệnh viện A;

B. Bệnh viện B;

C. Số lượng bệnh nhân khỏi bệnh của cả hai bệnh viện đều ổn định như nhau;

D. Số lượng bệnh nhân khỏi bệnh của cả hai bệnh viện đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

- Số lượng bệnh nhân khỏi bệnh trung bình của bệnh viện A là:

${\bar{x}}_{A} = \frac{15 + 32 + 44 + 24 + 20 + 29}{6} \approx 27, 33$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{A}^{2}$ = $\frac{1}{6}$ [(15 – 27,33)² + (32 – 27,33)² + (44 – 27,33)² + (24 – 27,33)² + (20 – 27,33)² + (29 – 27,33)²] ≈ 86,56.

Do đó phương sai của mẫu số liệu trên là 86,56.

Độ lệch chuẩn của mẫu số liệu trên là S_A = $\sqrt{S_{A}^{2}}$ = $\sqrt{86, 56}$ ≈ 9,3.

- Số giờ trung bình sử dụng Internet của bạn Ngân là:

${\bar{x}}_{B} = \frac{20 + 25 + 33 + 15 + 26 + 30}{6} \approx 24, 83$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{B}^{2}$ = $\frac{1}{6}$ [(20 – 24,83)² + (25 – 24,83)² + (33 – 24,83)² + (15 – 24,83)² + (26 – 24,83)² + (30 – 24,83)² ] ≈ 35,81.

Do đó phương sai của mẫu số liệu trên là 35,81.

Độ lệch chuẩn của mẫu số liệu trên là S_B = $\sqrt{S_{B}^{2}} = \sqrt{35, 81}$ ≈ 5,98.

Ta thấy phương sai và độ lệch chuẩn trong số lượng bệnh nhân khỏi bệnh của bệnh viện B bé hơn bệnh viện A nên số lượng bệnh nhân khỏi bệnh của bệnh viện B ổn định hơn.

Câu 7:

Một đại lý bán mắt kính mở thêm 2 cơ sở để bán. Số lượng mắt kính bán được ở 2 cơ sở trong 10 ngày đầu khai trương được thống kê trong bảng dưới đây:

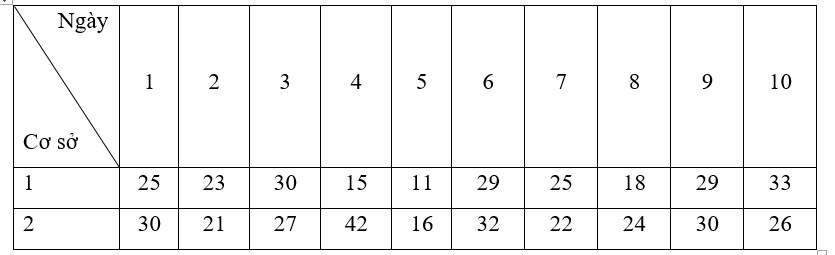
Một đại lý bán mắt kính mở thêm 2 cơ sở để bán. Số lượng mắt kính bán được ở 2 cơ sở (ảnh 1)

Sử dụng kiến thức về khoảng biến thiên và khoảng tứ phân vị, xác định xem số lượng mắt kính bán được của cơ sở nào ổn định hơn?

A. Cơ sở 1;

B. Cơ sở 2;

C. Số lượng mắt kính bán được của cả hai cơ sở đều ổn định như nhau;

D. Không kết luận được.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

- Sắp xếp số lượng mắt kính bán được của cơ sở 1 theo thứ tự không giảm ta có:

11; 15; 18; 23; 25; 25; 29; 29; 30; 33.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 11

+ Giá trị lớn nhất của mẫu số liệu trên là 33

Suy ra khoảng biến thiên R₁ = 33 – 11 = 22.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 11; 15; 18; 23; 25.

Do đó Q₁ = 18.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 25; 29; 29; 30; 33.

Do đó Q₃ = 29.

Suy ra khoảng tứ phân vị ∆_Q1 = Q₃ – Q₁ = 29 – 18 = 11.

- Sắp xếp số lượng mắt kính bán được của cơ sở 2 theo thứ tự không giảm ta có:

16; 21; 22; 24; 26; 27; 30; 30; 32; 42.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 16

+ Giá trị lớn nhất của mẫu số liệu trên là 42

Suy ra khoảng biến thiên R₂ = 42 – 16 = 26.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 16; 21; 22; 24; 26.

Do đó Q_1' = 22.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 27; 30; 30; 32; 42.

Do đó Q_3' = 30.

Suy ra khoảng tứ phân vị ∆_Q2 = Q_3' – Q_1' = 30 – 22 = 8.

Ta thấy:

+ Khoảng biến thiên trong số lượng mắt kính bán được của cơ sở 1 bé hơn cơ sở 2.

+ Khoảng tứ phân vị trong số lượng mắt kính bán được của cơ sở 1 lớn hơn cơ sở 2.

Do đó, với kiến thức về khoảng biến thiên và khoảng tứ phân vị, ta không kết luận được số lượng mắt kính bán được của cơ sở nào ổn định hơn.

Câu 8:

Một đại lý bán mắt kính mở thêm 2 cơ sở để bán. Số lượng mắt kính bán được ở 2 cơ sở trong 10 ngày đầu khai trương được thống kê trong bảng dưới đây:

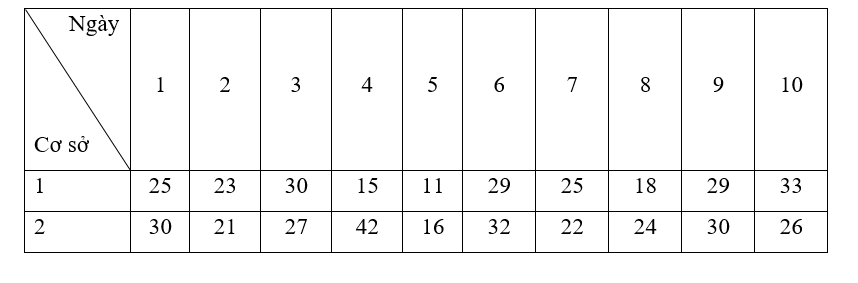
Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem số lượng mắt kính bán được của cơ sở nào ổn định hơn?

A. Cơ sở 1;

B. Cơ sở 2;

C. Số lượng mắt kính bán được của cả hai cơ sở đều ổn định như nhau;

D. Không kết luận được.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

- Số trung bình mắt kính bán được của cơ sở 1 là:

${\bar{x}}_{1} = \frac{25 + 23 + 30 + 15 + 11 + 29 + 25 + 18 + 29 + 23}{10} = 23, 8$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{1}^{2}$ = $\frac{1}{10}$ [(25 – 23,8)² + (23 – 23,8)² + (30 – 23,8)² + (15 – 23,8)² + (11 – 23,8)² + (29 – 23,8)² + (25 – 23,8)² + (18 – 23,8)² + (29 – 23,8)² + (23 – 23,8)² ] = 45,56.

Do đó phương sai của mẫu số liệu trên là 45,56.

Độ lệch chuẩn của mẫu số liệu trên là S₁ = $\sqrt{S_{1}^{2}}$ = $\sqrt{45, 56}$ ≈ 6,75.

- Số giờ trung bình sử dụng Internet của bạn Ngân là:

${\bar{x}}_{2} = \frac{30 + 21 + 27 + 42 + 16 + 32 + 22 + 24 + 30 + 26}{10} = 27$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{2}^{2}$ = $\frac{1}{10}$ [(30 – 27)² + (21 – 27)² + (27 – 27)² + (42 – 27)² + (16 – 27)² + (32 – 27)² + (22 – 27)² + (24 – 27)² + (30 – 27)² + (26 – 27)²] = 46.

Do đó phương sai của mẫu số liệu trên là 46.

Độ lệch chuẩn của mẫu số liệu trên là S₂ = $\sqrt{S_{2}^{2}}$ = $\sqrt{46}$ ≈ 6,78.

Ta thấy phương sai và độ lệch chuẩn trong số lượng mắt kính bán được của cơ sở 1 bé hơn cơ sở 2 nên số lượng mắt kính bán được của cơ sở 1 ổn định hơn.

Câu 9:

Số lượng học sinh đạt giải cuộc thi Học sinh giỏi tỉnh của 2 trường A và B từ năm 2016 – 2021 được thống kê trong bảng dưới đây:

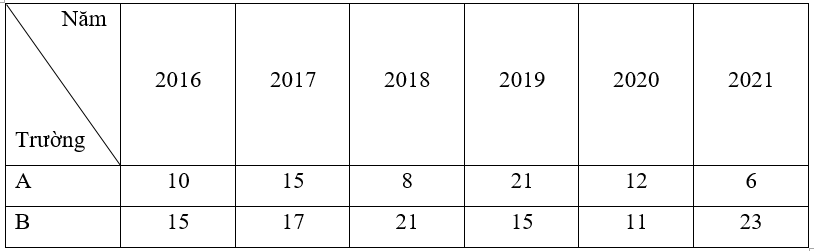
Số lượng học sinh đạt giải cuộc thi Học sinh giỏi tỉnh của 2 trường A và B từ năm 2016 – 2021 (ảnh 1)

Sử dụng kiến thức về khoảng biến thiên và khoảng tứ phân vị, xác định xem số lượng học sinh đạt giải của trường nào ổn định hơn?

A. Trường A;

B. Trường B;

C. Số lượng học sinh đạt giải của cả hai trường đều ổn định như nhau;

D. Số lượng học sinh đạt giải của cả hai trường đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

- Sắp xếp số lượng học sinh đạt giải của trường A theo thứ tự không giảm ta có:

6; 8; 10; 12; 15; 21.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 6.

+ Giá trị lớn nhất của mẫu số liệu trên là 21.

Suy ra khoảng biến thiên R_A = 21 – 6 = 15.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 6; 8; 10.

Do đó Q_1A = 8.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 12; 15; 21.

Do đó Q_3A = 15.

Suy ra khoảng tứ phân vị ∆_QA = Q_3A – Q_1A = 15 – 8 = 7.

- Sắp xếp số lượng học sinh đạt giải của trường B theo thứ tự không giảm ta có:

11; 15; 15; 17; 21; 23.

+ Giá trị nhỏ nhất của mẫu số liệu trên là 11

+ Giá trị lớn nhất của mẫu số liệu trên là 23

Suy ra khoảng biến thiên R_B = 23 – 11 = 12.

Ta lại có:

+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 11; 15; 15.

Do đó Q_1B = 15.

+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 17; 21; 23.

Do đó Q_3B = 21.

Suy ra khoảng tứ phân vị ∆_QB = Q_3B – Q_1B = 21 – 15 = 6

Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số lượng học sinh đạt giải của trường B bé hơn trường A nên số lượng đạt giải của trường B ổn định hơn.

Câu 10:

Số lượng học sinh đạt giải cuộc thi Học sinh giỏi tỉnh của 2 trường A và B từ năm 2016 – 2021 được thống kê trong bảng dưới đây:

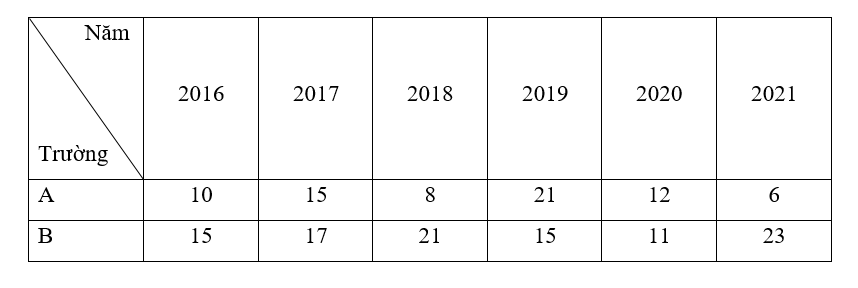
Số lượng học sinh đạt giải cuộc thi Học sinh giỏi tỉnh của 2 trường A và B từ năm (ảnh 1)

Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem số lượng học sinh đạt giải của trường nào ổn định hơn?

A. Trường A;

B. Trường B;

C. Số lượng học sinh đạt giải của cả hai trường đều ổn định như nhau;

D. Số lượng học sinh đạt giải của cả hai trường đều không ổn định.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

- Số trung bình học sinh đạt giải trong các năm 2016 – 2021 của trường A là:

${\bar{x}}_{A} = \frac{10 + 15 + 8 + 21 + 12 + 6}{6} = 12$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{A}^{2}$ = $\frac{1}{6}$ [(10 – 12)² + (15 – 12)² + (8 – 12)² + (21 – 12)² + (12 – 12)² + (6 – 12)²] ≈ 24,33.

Do đó phương sai của mẫu số liệu trên là 24,33.

Độ lệch chuẩn của mẫu số liệu trên là S_A = $\sqrt{S_{A}^{2}}$ = $\sqrt{24, 33}$ ≈ 4,93.

- Số giờ trung bình sử dụng Internet của bạn Ngân là:

$\bar{x_{B}} = \frac{15 + 17 + 21 + 15 + 11 + 23}{6} = 17$

Công thức tính phương sai của một mẫu số liệu là:

S² = $\frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ... + {(x_{n} - \bar{x})}^{2}]$

Thay số ta có:

$S_{B}^{2}$ = $\frac{1}{6}$ [(15 – 17)² + (17 – 17)² + (21 – 17)² + (15 – 17)² + (11 – 17)² + (23 – 17)² ] = 16.

Do đó phương sai của mẫu số liệu trên là 16.

Độ lệch chuẩn của mẫu số liệu trên là S_B = $\sqrt{S_{B}^{2}} = \sqrt{16}$ = 4.

Ta thấy phương sai và độ lệch chuẩn trong số lượng học sinh đạt giải của trường B bé hơn trường A nên số lượng đạt giải của trường B ổn định hơn.