10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 CTST Bài tập cuối chương 6 có đáp án (Phần 2) (Vận dụng)

Câu 1:

Cho số a = $\frac{2}{7}$ và các giá trị gần đúng của a là 0,28; 0,29; 0,286; 0,2861. Hỏi giá trị gần đúng nào là tốt nhất?

A. 0,28;

B. 0,29;

C. 0,286;

D. 0,2861.

Xem đáp án

Đáp án đúng là: D

Ta có các sai số tuyệt đối là:

$Δ_{1} = |\frac{2}{7} - 0,28| = \frac{1}{175}$ ;

$Δ_{2} = |\frac{2}{7} - 0,29| = \frac{3}{700}$ ;

$Δ_{3} = |\frac{2}{7} - 0,286| = \frac{1}{3500}$ ;

$Δ_{4} = |\frac{2}{7} - 0,2861| = \frac{27}{70000}$ .

Ta thấy ∆4 nhỏ nhất nên số 0,2861 là số gần đúng tốt nhất.

Câu 2:

Một tấm thép hình chữ nhật có chiều dài là: a = 20 m ± 0,01 m và chiều rộng b = 15 m ± 0,01 m. Chu vi P của tấm thép đó là:

A. P = 70 m ± 0,01 m;

B. P = 70 m ± 0,02 m;

C. P = 70 m ± 0,03 m;

D. P = 70 m ± 0,04 m.

Xem đáp án

Đáp án đúng là: D

Cách 1:

Nửa chu vi của tấm thép hình chữ nhật trên là:

(20 ± 0,01) + (15 ± 0,01) = (20 + 15) ± (0,01 + 0,01)

= 35 ± 0,02 (m).

Khi đó chu vi của tấm thép hình chữ nhật trên là:

2 . (35 ± 0,02) = 70 ± 0,04 (m).

Vậy P = 70 m ± 0,04 m.

Cách 2:

Gọi chiều dài và chiều rộng chính xác của tấm thép hình chữ nhật trên là x, y (x, y > 0) (m).

Khi đó ta có: x = 20 + i và y = 15 + j với – 0,01 ≤ i, j ≤ 0,01.

Chu vi là: P = 2 (x + y) = 2. [(20 + i) + (15 + j)] = 2. (35 + i + j)

P = 70 + 2. (i + j)

Ta có: – 0,01 ≤ i, j ≤ 0,01 suy ra –0,04 ≤ 2. (i + j) ≤ 0,04.

Vậy P = 70 m ± 0,04 m.

Câu 3:

Hình chữ nhật có các cạnh x = 2 m ± 1 cm, y = 5 m ± 2 cm. Sai số tương đối của diện tích hình chữ nhật đó là?

A. 0,5%;

B. 0,4%;

C. 0,9%;

D. 9%.

Xem đáp án

Đáp án đúng là: C

Diện tích gần đúng của hình chữ nhật là: S = 2 . 5 = 10 (m2).

Giá trị lớn nhất của diện tích hình chữ nhật là:

(2 + 0,01) . (5 + 0,02) = 10,0902 (m2).

Giá trị nhỏ nhất của diện tích hình chữ nhật là:

(2 – 0,01) . (5 – 0,02) = 9,9102 (m2).

Ta có: 9,9102 – S ≤ $\bar{S} - S$ ≤ 10,0902 – S

Hay 9,9102 – 10 ≤ $\bar{S} - 10$ ≤ 10,0902 – 10

Do đó 0,0898 ≤ $\bar{S} - S$ ≤ 0,0902 nên $|S - \bar{S}| \leq 0,0898$ .

Sai số tuyệt đối là: $Δ_{s} = |S - \bar{S}| \leq 0,0898$ .

Sai số tương đối là: $δ_{S} = \frac{Δ_{S}}{|S|} \leq \frac{0,0898}{10} \approx 0,9 %$ .

Vậy ta chọn C.

Câu 4:

Cho hai biểu đồ sau:

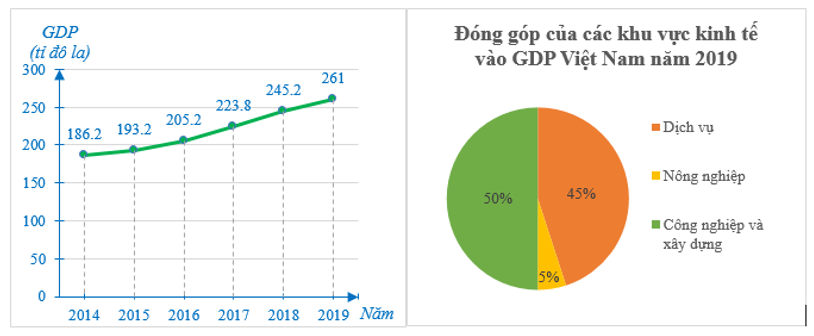
Năm 2019 khu vực Dịch vụ đóng góp vào GDP Việt Nam là bao nhiêu?

A. 117,44 tỉ đô la;

B. 117,45 tỉ đô la;

C. 117,46 tỉ đô la;

D. 117,8 tỉ đô la.

Xem đáp án

Đáp án đúng là: B

Dựa vào biểu đồ thứ nhất, ta biết được GDP Việt Nam năm 2019 là 261 tỉ đô la.

Năm 2019 khu vực Dịch vụ đóng góp vào GDP Việt Nam là: $\frac{261. 45}{100} = 117,45$ (tỉ đô la).

Vậy ta chọn phương án B.

Câu 5:

Một cửa hàng bán hoa vào ngày 8 tháng 3 (Quốc tế phụ nữ) thống kê được như sau:

Loại hoa	Hoa cúc họa mi	Hoa hồng vàng	Hoa hồng	Hoa voan
Số bông	15	29	30	11

Hỏi cửa hàng nên nhập loại hoa nào để bán trong những dịp lễ tương tự?

A. Hoa cúc họa mi;

B. Hoa hồng vàng;

C. Hoa hồng;

D. Hoa voan.

Xem đáp án

Đáp án đúng là: C

Ta thấy số hoa hồng bán được là nhiều nhất (30 > 29 > 15 > 11).

Do đó Mo là hoa hồng.

Vậy cửa hàng nên nhập loại hoa hồng để bán trong những dịp lễ tương tự.

Câu 6:

Số hạt của một số loại cây nảy mầm thành cây non trong 1 000 hạt được gieo trong 10 lần khác nhau thống kê như sau:

50

120

20

800

400

200

25

220

160

350

Trong trường hợp này, ta nên chọn số nào dưới đây làm giá trị đại diện là tốt nhất? Tính giá trị đại diện đó.

A. Số trung bình,

\bar{x}

= 235;

B. Trung vị, Me = 200;

C. Số trung bình,

\bar{x}

= 80;

D. Trung vị, Me = 180.

Xem đáp án

Đáp án đúng là: D

Ta nên chọn số trung vị làm đại diện là tốt nhất vì có sự chênh lệch lớn giữa các số liệu trong mẫu. Do đó ta có thể loại phương án A và C.

Sắp xếp mẫu dữ liệu trên theo thứ tự không giảm, ta được:

20; 25; 50; 120; 160; 200; 220; 350; 400; 800.

Vì cỡ mẫu n = 10 là số chẵn nên trung vị của mẫu là trung bình cộng của số liệu thứ 5 và thứ 6.

Do đó Me = (160 + 200) : 2 = 180.

Vậy ta chọn phương án D.

Câu 7:

Số lượng xe máy đi lại trên đường Phạm Ngũ Lão trong các khung giờ được thống kê lại như sau:

40	80	35	40	30	100	10
25	35	45	5	20	15	70

Hỏi mật độ số liệu tập trung chủ yếu ở đâu?

A. Bên trái Q2;

B. Bên phải Q2;

C. Số liệu dàn trải đều;

D. Không thể biết được mật độ số liệu tập trung chủ yếu ở đâu.

Xem đáp án

Đáp án đúng là: B

Sắp xếp lại mẫu số liệu theo thứ tự không giảm ta được:

5; 10; 15; 20; 25; 30; 35; 35; 40; 40; 45; 70; 80;100.

- Vì cỡ mẫu n = 14 là số chẵn, nên giá trị tứ phân vị thứ hai là trung bình cộng của số thứ 7 và thứ 8 tức là Q2 = (35 + 35) : 2 = 35.

- Tứ phân vị thứ nhất là trung vị của mẫu: 5; 10; 15; 20; 25; 30; 35. Do đó Q1 = 20.

- Tứ phân vị thứ ba là trung vị của mẫu: 35; 40; 40; 45; 70; 80; 100. Do đó Q3 = 45.

Ta có Q2 – Q1 = 35 – 20 = 15 và Q3 – Q2 = 45 – 35 = 10.

Vì 15 > 10 nên khoảng cách giữa Q1 và Q2 lớn hơn khoảng cách giữa Q2 và Q3.

Ta suy ra mật độ số liệu ở bên trái Q2 thấp hơn ở bên phải Q2.

Vậy ta chọn phương án B.

Câu 8:

Bạn An khi thi chứng chỉ Tiếng Anh đã đạt được IELTS 7.0, bạn đã thống kê điểm các số 4 kỹ năng như bảng dưới đây tuy nhiên lại không nhớ điểm kỹ năng Viết được bao nhiêu điểm.

Kỹ năng	Nghe	Nói	Đọc	Viết
Điểm	7,5	7,0	7,0	?

Biết rằng:

- Điểm các kỹ năng chỉ tính .5 và .0;

- Thang điểm của IELTS sẽ được tính dựa trên điểm trung bình cộng của 4 kỹ năng. Điểm tổng của 4 kỹ năng sẽ được làm tròn số theo quy ước chung như sau:

+ Nếu điểm trung bình cộng của 4 kỹ năng có số lẻ là .25, thì sẽ được làm tròn lên thành .5;

+ Nếu điểm trung bình cộng của 4 kỹ năng có số lẻ là .75 sẽ được làm tròn thành 1.0.

Em hãy giúp bạn An xác định điểm kỹ năng Viết của bạn ấy.

A. x ∈ {5,5; 6,0; 6,5; 7,0};

B. x ∈ {5,0; 5,5; 6,0; 6,5};

C. x ∈ {5,0; 5,5; 6,0; 6,5; 7,0};

D. x ∈ {4,5; 5,0; 5,5; 6,0; 6,5; 7,0}.

Xem đáp án

Đáp án đúng là: C

Gọi điểm kỹ năng Viết của bạn An là x.

Điểm IELTS của bạn An được tính như sau:

$\bar{x} = \frac{7,5 + 7,0 + 7,0 + x}{4} = \frac{x + 21,5}{4}$ .

Do điểm IELTS của bạn An đạt 7.0, nên theo quy ước làm tròn được nêu ở đề bài thì điểm trung bình 4 kỹ năng của bạn An phải thỏa mãn: $6,5 < \bar{x} < 7,5$

Do đó $6,5 < \frac{x + 21,5}{4} < 7,5$

Suy ra 26 < x + 21,5 < 30

Hay 4,5 < x < 8,5.

Mà điểm các kỹ năng chỉ tính .5 và .0

Nên x ∈ {5,0; 5,5; 6,0; 6,5; 7,0}.

Vậy ta chọn phương án C.

Câu 9:

Số lượng mũi tiêm trung bình được sử dụng trong 1 giờ của các ngày của bệnh viện Y Hà Nội được thống kê trong bảng sau:

Ngày	1	2	3	4	5	6	7
Số lượng	25	30	30	20	10	40	35

Ngày nào có số lượng mũi tiêm bất thường?

A. Ngày 1;

B. Ngày 5;

C. Ngày 6;

D. Không có ngày nào.

Xem đáp án

Đáp án đúng là: D

Sắp xếp mẫu số liệu số lượng mũi tiêm trung bình được sử dụng trong 1 giờ của các ngày của bệnh viện Y Hà Nội ta có: 10; 20; 25; 30; 30; 35; 40.

• Do mẫu có n = 7 là số lẻ nên có tứ phân vị thứ hai là số liệu thứ 4, tức là Q2 = 30.

• Tứ phân vị thứ nhất là trung vị của mẫu 10; 20; 25.

Do mẫu trên có cỡ mẫu là 3 (số lẻ) nên Q1 = 20.

• Tứ phân vị thứ ba là trung vị của mẫu 30; 35; 45.

Do mẫu trên có cỡ mẫu là 3 (số lẻ) nên Q3 = 35.

Khi đó khoảng tứ phân vị là: DQ = Q3 – Q1 = 35 – 20 = 15.

Ta có Q1 – $\frac{3}{2}$ DQ = ‒ 2,5 và Q3 + $\frac{3}{2}$ DQ = 57,5.

Vậy ta chọn phương án D.

Câu 10:

Cho bảng số liệu biểu diễn thời gian hoàn thành bài chạy 100 m (tính theo giây) của 3 bạn Minh, Bình, Đức trong 9 lần thi thử như dưới đây:

Bạn Minh	12	13	16	12	11	12	12	15	14
Bạn Bình	15	15	16	18	14	14	13	13	12
Bạn Đức	15	10	10	12	19	14	12	11	11

Bạn nào có “phong độ chạy ổn định” nhất?

A. Bạn Minh;

B. Bạn Bình;

C. Bạn Đức;

D. Không xác định được.

Xem đáp án

Đáp án đúng là: A

• Đối với bạn Minh:

${\bar{x}}_{1} = \frac{12 + 13 + 16 + 12 + 11 + 12 + 12 + 15 + 14}{9} = 13$

$S_{1}^{2} = \frac{1}{9} (12^{2} + 13^{2} + 16^{2} + 12^{2} + 11^{2} + 12^{2} + 12^{2} + 15^{2} + 14^{2}) - 13^{2} = \frac{22}{9} \approx 2,4$

• Đối với bạn Bình:

${\bar{x}}_{2} = \frac{15 + 15 + 16 + 18 + 14 + 14 + 13 + 13 + 12}{9} = \frac{130}{9}$

$S_{2}^{2} = \frac{1}{9} (15^{2} + 15^{2} + 16^{2} + 18^{2} + 14^{2} + 14^{2} + 13^{2} + 13^{2} + 12^{2}) - {(\frac{130}{9})}^{2} = \frac{236}{81} \approx 2,9$

• Đối với bạn Đức:

$\frac{15 + 10 + 10 + 12 + 19 + 14 + 12 + 11 + 11}{9} = \frac{38}{3}$

$S_{1}^{2} = \frac{1}{9} (15^{2} + 10^{2} + 10^{2} + 12^{2} + 19^{2} + 14^{2} + 12^{2} + 11^{2} + 11^{2}) - {(\frac{38}{3})}^{2} = \frac{68}{9} \approx 7,6$

Ta thấy phương sai mẫu số liệu của bạn Minh nhỏ nhất nên bạn Minh chạy ổn định nhất.