Đề thi Học kì 1 Toán 10 Cánh diều có đáp án - Đề 2
-
1707 lượt thi
-
28 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trục đối xứng của parabol y = x2 + 3x – 1 là đường thẳng:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Parabol y = x2 + 3x – 1 có trục đối xứng là đường thẳng .
Câu 2:
Cho α là góc nhọn. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Vì α là góc nhọn nên sinα > 0 và cosα > 0
⇒ cotα =
Vậy chọn đáp án B.
Câu 3:
Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là C
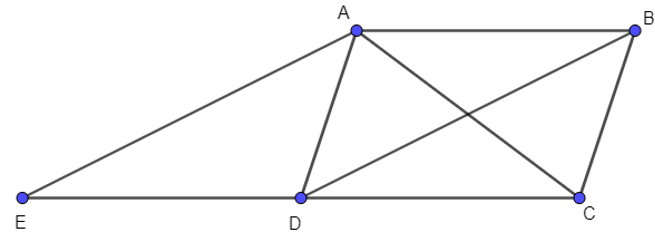
Lấy điểm E sao cho ABDE là hình bình hành, khi đó ,
Suy ra AB = ED mà AB = CD nên DE = DC hay D là trung điểm của EC.
Ta có: (quy tắc hình bình hành).Câu 4:
Cho tam giác ABC vuông tại A, AB = 2, . Độ dài của vectơ gần với giá trị nào nhất sau đây:.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
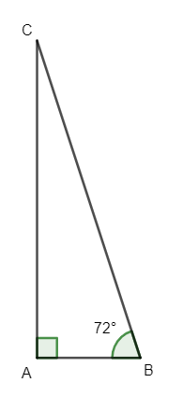
Ta có:
⇒
Xét tam giác ABC vuông tại A có:
cosB =
⇔ cos72° =
⇔ BC = .
Vậy độ dài của vectơ gần vớ 6,5.
Câu 5:
Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là:
A. ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0;
B. ∀x ∈ ℝ, x3 – 2x + 1 < 0”;
C. ∃x ∈ ℝ, x3 – 2x + 1 ≥ 0”;
D. ∀x ∈ ℝ, x3 – 2x + 1 > 0”.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0.
Câu 6:
Cho hai vectơ đều khác vectơ Tích vô hướng của và được xác định bởi công thức
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Tích vô hướng của và được xác định bởi công thức
Câu 7:
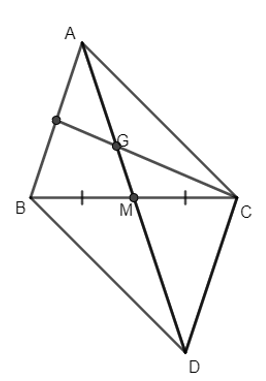
Cho hình bình hành ABCD, có M là trung điểm của BC, G là trọng tâm của tam giác ABC (tham khảo hình vẽ bên). Khi đó . Vậy k bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Vì G là trọng tâm tam giác ABC nên ta có: .
Mặt khác ABCD là hình bình hành, M là trung điểm của BC nên
⇒ hay .
Vậy k = 3.
Câu 8:
Cho hai tập hợp A = {– 3; – 1; 1; 2; 4; 5} và B = {– 2; – 1; 0; 2; 3; 5}. Tập hợp A\B:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có tập hợp A \ B là tập hợp các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B nên khi đó ta có: A \ B = {– 3; 1; 4}.
Câu 9:
Tập hợp A = {x ∈ ℝ| – 2 ≤ x < 0} viết lại dưới dạng khác là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta có: A = {x ∈ ℝ| – 2 ≤ x < 0} = [– 2; 0).
Câu 10:
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
Câu 11:
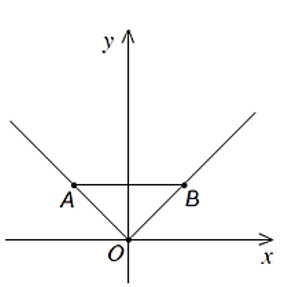
Hai điểm A, B nằm trên đồ thị hàm số y = |x| và đối xứng với nhau qua trục tung. Biết , diện tích S của tam giác OAB là (biết O là gốc tọa độ, tham khảo đồ thị hàm số y = |x| ở hình vẽ bên).
 Xem đáp án
Xem đáp án
Đáp án đúng là B
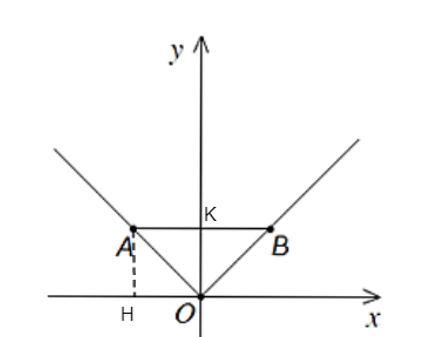
Vì A và B đối xứng với nhau qua Oy nên AB ⊥ Oy
Mà Ox ⊥ Oy nên AB // Ox
Kẻ AH vuông góc với Ox và gọi K là trung điểm của AB.
Ta có nên AK = KB = hay OH = . Suy ra xA = .
Mặt khác A thuộc vào đồ thị hàm số nên yA = |xA| = .
⇒ OK =
Diện tích tam giác OAB là: SOAB = (đvdt).
Vậy diện tích tam giác OAB là .
Câu 13:
Cho hình vuông ABCD. Có bao nhiêu vectơ cùng phương với vectơ :
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Các vectơ cùng phương là các vectơ có giá song song hoặc trùng nhau. Do đó các vectơ cùng phương với vectơ là: , , .
Vậy có 3 vec tơ cùng phương với vectơ .
Câu 14:
Giá trị nào dưới đây là nghiệm của phương trình ?
A. x = 0;
B. x = – 1;
C. x = 0 và x = – 1;
D. Không tồn tại x là nghiệm của phương trình.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Xét phương trình
⇔ = – 1 – x (điều kiện – 1 – x ≥ 0 ⇔ x ≤ – 1)
⇔ 1 – x2 = x2 + 2x + 1
⇔ 2x2 + 2x = 0
⇔ ⇔
Vậy x = – 1 là nghiệm của phương trình đã cho.
Câu 15:
Cho tam giác ABC vuông tại A, AB = 2, AC = 5, .Tính :
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có
.Câu 16:
Cho parabol (P):
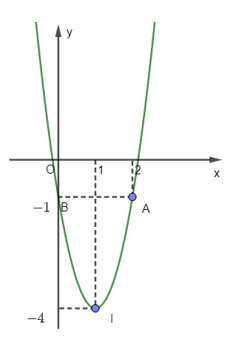
Hình vẽ trên là đồ thị của hàm số bậc hai nào dưới đây:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Gọi hàm số cần tìm có dạng y = ax2 + bx + c (a ≠ 0)
Quan sát hình vẽ ta có:
- Đồ thị hàm số cắt trục Oy tại điểm B(0; – 1) nên thay tọa độ điểm B vào hàm số ta được c = – 1.
- Tọa độ điểm đỉnh I(1; – 4)
Khi đó:
Và
Thay b = – 2a vào biểu thức trên ta được: 4a2 + 4a = 16a ⇔ 4a2 – 12a = 0 ⇔ a = 0 (không TM) hoặc a = 3 (TM).
⇒ b = – 2.3 = – 6 .
Vậy hàm số cần tìm là: y = 3x2 – 6x – 1.
Câu 17:
Hàm số nào sau đây là hàm số lẻ?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
+) Xét hàm số f(x) = x3 + 1
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = (– x)3 + 1 = – x3 + 1.
Do đó f(x) không chẵn cũng không lẻ.
+) Xét hàm số f(x) = 2x4 + 3
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = 2(– x)4 + 3 = 2x4 + 3 = f(x).
Do đó f(x) là hàm chẵn.
+) Xét hàm số f(x) = |x|
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = |– x| = |x| = f(x).
Do đó f(x) là hàm chẵn.
+) Xét hàm số f(x) = x3
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = (– x)3 = – x3 = – f(x).
Do đó f(x) là hàm lẻ.
Câu 18:
Trong các phát biểu sau, phát biểu nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Xét phương trình
Điều kiện xác định f(x) ≥ 0 hoặc g(x) ≥ 0
Bình phương hai vế của phương trình đã cho ta được: f(x) = g(x)
Vì vậy tập nghiệm của phương trình là tập hợp các nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).
Câu 19:
Cho tứ giác ABCD. Xác định điểm M thỏa mãn:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Gọi G là trọng tâm tam giác BCD, khi đó ta có:
Ta có:
⇔
⇔
⇔
⇔
Vậy M là trung điểm của GA.
Câu 20:
Cho tứ giác ABC có AB = 5, AC = 4, . Khi đó độ dài BC khoảng:
A. 42,4;
B. 6,5;
C. 3;
D. 3,2.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Xét tam giác ABC, có:
BC2 = AB2 + AC2 – 2AB.AC.cos
= 42 + 52 – 2.4.5.cos92°
≈ 42,4
⇒ BC = 6,5
Vậy BC = 6,5.
Câu 21:
Gọi S là tập nghiệm của bất phương trình – x2 + 2x – 4 ≤ 0. Khi đó S bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Xét bất phương trình – x2 + 2x – 4 ≤ 0 có a = – 1 < 0 và ∆’ = (– 1)2 – (– 1)(– 4) = – 3 < 0.
Dựa vào định lí dấu tam thức bậc hai ta có – x2 + 2x – 4 ≤ 0 ∀x
Vậy tập nghiệm của bất phương trình là S = ℝ.
Câu 22:
Cho hệ bất phương trình . Điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Xét hệ bất phương trình
Thay lần lượt tọa độ các điểm M, N, P, Q vào hệ bất phương trình ta có:
Tọa độ điểm M không thỏa mãn BPT (3);
Tọa độ điểm N không thỏa mãn BPT (2);
Tọa độ điểm P không thỏa mãn BPT (3);
Tọa độ điểm Q thỏa mãn tất cả các BPT của hệ nên thuộc vào miền nghiệm.
Vậy chọn D.
Câu 23:
Với giá trị nào của tham số m thì tam thức f(x) = – x2 – 3x + m – 5 không dương với mọi x:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Xét tam thức f(x) = – x2 – 3x + m – 5 có a = – 1 và ∆ = (– 3)2 – 4.(– 1).(m – 5) = 9 + 4m – 20 = 4m – 11.
Để tam thức f(x) = – x2 – 3x + m – 5 không dương với mọi x thì ∆ ≤ 0
⇔ 4m – 11 ≤ 0
⇔ m ≤
Vậy m = 2 thỏa mãn điều kiện bài toán.
Câu 24:
Dựa vào đồ thị hàm số bậc hai y = f(x) (như hình vẽ) hãy tìm tập nghiệm của bất phương trình f(x) > 0:
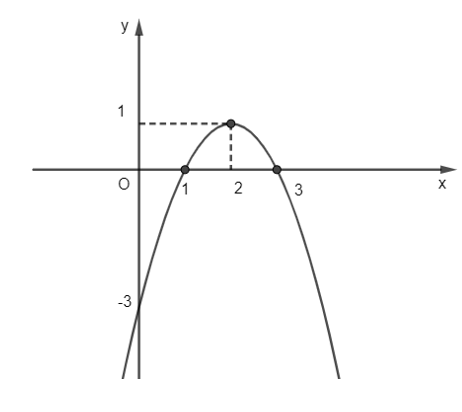
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Quan sát hình vẽ ta thấy với x ∈ (1; 3) thì đồ thị hàm số nằm phía trên trục hoành.
Hay f(x) > 0 khi x ∈ (1; 3).
Vậy tập nghiệm của bất phương trình f(x) > 0 là S = (1; 3).
Câu 25:
Nếu hai điểm M và N thỏa mãn: thì độ dài đoạn MN bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có:
Suy ra – MN2 = – 16 ⇔ MN =
Vậy MN = 4.
Câu 26:
a) Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 – 5x.
 Xem đáp án
Xem đáp án
a) Xét hàm số y = x2 – 5x, có: a = 1, b = – 5, c = 0 và ∆ = (– 5)2 – 4.1.0 = 25
Khi đó, ta có:
- Điểm đỉnh I có xI = ; yI = ;
- a = 1 > 0 .
Do đó ta có bảng biến thiên sau:
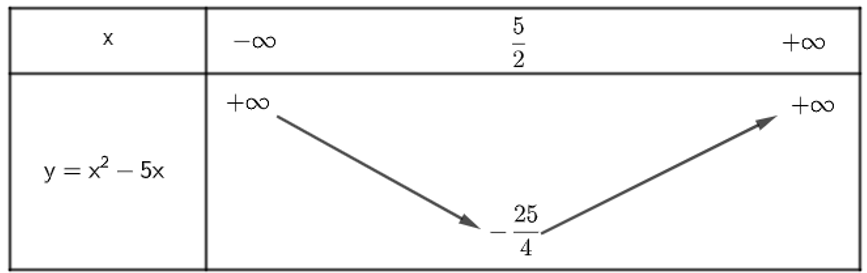
Vậy hàm số sẽ đồng biến trên khoảng , hàm số sẽ nghịch biến trên khoảng .
Câu 27:
b) Tìm các giá trị của tham số m để phương trình có một nghiệm duy nhất.
 Xem đáp án
Xem đáp án
b) Xét phương trình (*)
Điều kiện x + 1 ≥ 0 ⇔ x ≥ – 1
(*) ⇔ x2 – (2m – 1)x – m2 + 5m + = x2 + 2x + 1
⇔ (2m + 1)x + m2 – 5m – = 0
+) TH1: 2m + 1 = 0 ⇔ m = . Khi đó ta có:
= 0
⇔ 0.x + 0 = 0 (luôn đúng) với mọi x ≥ – 1
Do đó m = thỏa mãn.
+) TH1: 2m + 1 ≠ 0 ⇔ m ≠ . Khi đó ta có:
(2m + 1)x + m2 – 5m – = 0
⇔ x =
Để phương trình có nghiệm thì
⇔ m2 – 5m – ≥ – 2m – 1
⇔ m2 – 3m – ≥ 0
Xét tam thức bậc hai f(m) = m2 – 3m – , có a = 1 và ∆ = (– 3)2 – 4.1. = 16 > 0 suy ra f(m) có hai nghiệm m1 = và m2 = .
Dựa vào định lí dấu tam thức bậc hai ta có:
f(m) ≥ 0 ⇔ m ≤ hoặc m ≥ .
Suy ra m < hoặc m ≥ .
Vậy với m ≤ hoặc m ≥ thì phương trình có nghiệm.
Câu 28:
Bác Nam muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 42 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông sao cho độ cao hai thành rãnh bằng nhau. Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 160 cm2. Bác Nam cần làm rãnh nước có độ cao ít nhất là bao nhiêu xăng – ti – mét để đảm bảo kĩ thuật?
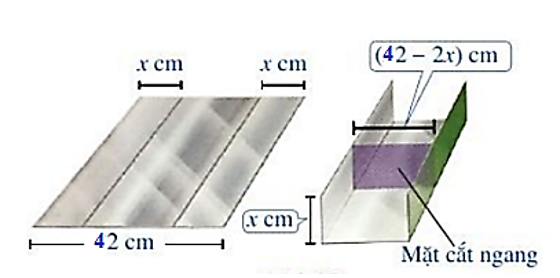
 Xem đáp án
Xem đáp án
Chia tấm tôn đó thành ba phần theo các kích thước x (cm), 42 – x (cm) và x (cm).
Khi gấp hai bên lại ta được rãnh dẫn nước có mặt cắt ngang có kích thước là x (cm) và 42 – x (cm).
Diện tích của mặt cắt ngang là x.(42 – x) = – x2 + 42x (cm2).
Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 160 cm2 nên ta có:
– x2 + 42x ≥ 160
⇔ – x2 + 42x – 160 ≥ 0
Xét tam thức bậc hai f(x) = – x2 + 42x – 160 có a = – 1, b = 42, c = – 160 và ∆ = 422 – 4.(– 1).(– 160) = 1124 > 0.
Suy ra f(x) có hai nghiệm x1 = và x2 = .
Áp dụng định lí dấu của tam thức bậc hai ta được:
f(x) ≥ 0 khi 2,12 ≤ x ≤ 18,88
Vậy rãnh nước phải có độ cao ít nhất khoảng 2,12 cm.
