Đề thi Học kì 1 Toán 10 Chân trời sáng tạo có đáp án- Đề 2
-
1054 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Câu nào sau đây không là mệnh đề?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Câu “Bạn học giỏi quá!” là câu cảm thán không xác định được tính đúng sai nên câu này không phải mệnh đề. Do đó A đúngCâu 2:
Tập xác định D của hàm số là
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Hàm số xác định khi và chỉ khi .
Do đó tập xác định của hàm số là: D = [– 2; 2] \ {0}.
Vậy đáp án đúng là A.
Câu 3:
Cho A = (– 1; 5] và B = (2; 7). Tập hợp A ∩ B bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có:
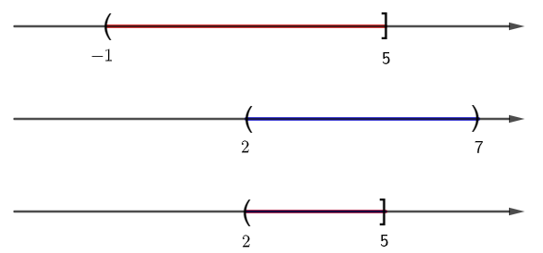
Khi đó A ∩ B = (2; 5].
Câu 4:
Cho tập hợp , . Tất cả giá trị của m để là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Để thì m – 1 > 1 ⇔ m > 2.
Câu 5:
Miền nghiệm của hệ bất phương trình là
 Xem đáp án
Xem đáp án
Miền nghiệm của hệ bất phương trình là miền trong tam giác không tô màu trong hình.
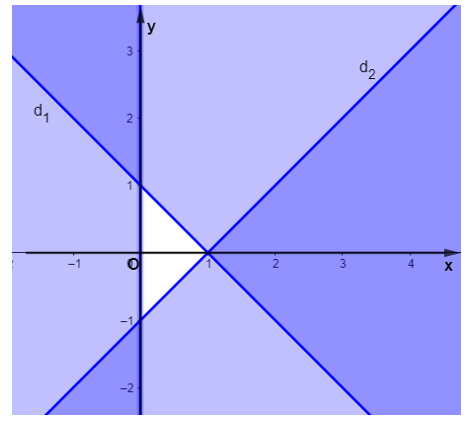
Câu 6:
Giá trị cos113° + cos45° + cos67° bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
cos113° + cos45° + cos67°
= cos(180° – 67°) + cos67° + cos45°
= – cos67° + cos67° + cos45°
= 0 +
= .
Câu 7:
Cho tam giác ABC có AC = 2, BC = 5 và . Số đo của góc A là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Áp dụng định lí sin trong tam giác ABC, ta được:
.
⇒ .
Câu 8:
Trong tam giácABC, khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Áp dụng định lí cosin trong tam giác ABC ta có:
.
Câu 9:
Cho hai vectơ và thỏa mãn và . Góc giữa hai vectơ và bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
.
Câu 10:
Cho hình vuông ABCD tâm O cạnh a Tính ta được :
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: BO =, BC = a và
Khi đó: .
Câu 11:
Cho = 12,096384. Số gần đúng của với độ chính xác d = 0,0004 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Hàng của chữ số khác 0 đầu tiên của độ chính xác là hàng phần chục nghìn. Quy tròn số đến hàng phần chục nghìn ta được số gần đúng của là: 12,0964.
Câu 12:
Cho hình vuông ABCD. Vectơ bằng vectơ nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vectơ cùng hướng với .
Câu 13:
Cho hình thang ABCD . Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hai vectơ cùng phương nhưng ngược hướng. Do đó C đúng và B sai.
Hai vectơ cùng hướng. Do đó D sai.
Hai vectơ không cùng phương. Do đó A sai.
Câu 14:
Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng x = 1 làm trục đối xứng là
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có:
Hàm số bậc hai y = – 2x2 + 4x + 1 có a = – 2, b = 4, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 + 4x + 3 có a = 2, b = 4, c = 3. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 – 2x + 1 có a = 2, b = – 2, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = x2 – x + 5 có a = 1, b = –1, c = 5. Khi đó trục đối xứng là x = .
Câu 15:
Cho hình bình hành ABCD . Đẳng thức vectơ nào sau đây đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Áp dụng quy tắc hình bình hành ta được: .
Câu 16:
Cho tam giác ABC vuông tại A, , M là trung điểm của BC và có . Tính cạnh AB, AC:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét tam giác ABC vuông tại A, có:
AM = BC = .
Ta có:
Xét tam giác ABM:
Áp dụng định lí cosin trong tam giác ABM, có:
AB2 = AM2 + BM2 – 2.AM.BM.
⇔ AB2 =
⇔ AB2 = a2
⇔ AB = a
Áp dụng định lí Pythagore trong tam giác ABC, ta được:
AC2 = BC2 – AB2 = 3a2 – a2 = 2a2
⇔ AC = a.
Vậy AB = a và AC = a.
Câu 17:
Cho số gần đúng là a = 1,2357 với độ chính xác là d = 0,01. Số quy tròn của số a là:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Hàng lớn nhất của độ chính xác là hàng phần trăm thì ta cần làm tròn đến hàng phần mười. Khi đó ta có số quy tròn của số gần đúng a là 1,2.
Câu 18:
Hàm số nào dưới đây là hàm nghịch biến với mọi x ∈ ℝ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hàm số y = ax + b nghịch biến trên ℝ khi a < 0. Do đó D đúng và A sai.
Hàm số y = – |x| vừa đồng biến và nghịch biến trên ℝ.
Hàm số y = x2 + 2x vừa đồng biến và nghịch biến trên ℝ.
Câu 19:
Cho các hàm số: f(x) = , g(x) = và h(x) = x2 – x. Trong các hàm số đã cho, số hàm chẵn là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
+) Xét hàm số: f(x) = , có TXĐ: D = [ – 1; +∞).
Lấy x ∈ D và – x ∈ D
Khi đó f(– x) = ≠ f(x).
Do đó hàm số không chẵn cũng không lẻ.
+) Xét hàm số g(x) = có TXĐ D = ℝ
Lấy x ∈ D và – x ∈ D
Khi đó: g( – x) = = – g(x).
Do đó hàm số đã cho là hàm lẻ.
+) Xét hàm số h(x) = x2 – x
Lấy x ∈ D và – x ∈ D
Khi đó: h( – x) = (– x)2 – (– x) = x2 + x ≠ h(x).
Do đó hàm số đã cho là hàm không chẵn cũng không lẻ.
Vậy không có hàm số nào chẵn.
Câu 20:
Cho hàm số y = (m – 2021)x + m – 2. Điều kiện để hàm số đồng biến trên ℝ là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là B
Để hàm số y = (m – 2021)x + m – 2 đồng biến trên ℝ khi m – 2021 > 0 ⇔ m > 2021.
Vậy với m > 2021 thì hàm số đồng biến trên ℝ.
Câu 21:
Cho bảng biến thiên sau:
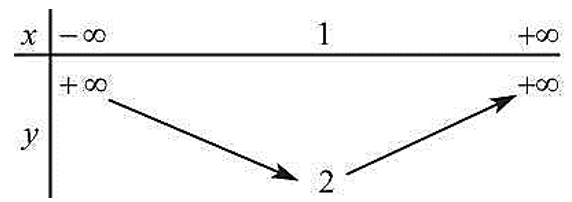
Đồ thị hàm số bậc hai tương ứng với bảng biến thiên trên là :
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Gọi hàm số bậc hai cần tìm là: y = ax2 + bx + c (với a, b, c ∈ ℝ, a ≠ 0)
Dựa vào bảng biến thiên ta thấy a > 0 nên đáp án D sai.
Ta có: xI = ⇔ b = – 2a. Do đó A sai.
Ta lại có: yI = ⇔ ∆ = – 8a ⇔ b2 – 4ac = – 8a ⇔ 4a2 – 4ac = – 8a ⇔ a – c = – 2 ⇔ c = a + 2
+) Nếu a = 1 thì b = – 2 và c = 3. Do đó B sai.
+) Nếu a = 2 thì b = – 4 và c = 4. Do đó C đúng.
Câu 22:
Cho hình chữ nhật ABCD tâm O. Gọi E, F lần lượt là trung điểm của OA và CD. Biết . Tính giá trị biểu thức a + b:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
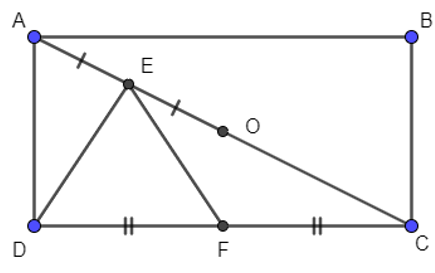
Ta có: (quy tắc hình bình hành)
.
Câu 23:
Giá trị ngoại lệ trong mẫu là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Giá trị ngoại lệ là giá trị quá nhỏ hoặc quá lớn so với các giá trị khác trong mẫu số liệu.
Câu 24:
Số liệu xuất hiện nhiều nhất trong mẫu số liệu được gọi là:
A. Số trung bình cộng;
B. Trung vị;
C. Tứ phân vị;
D. Mốt.
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Số liệu xuất hiện nhiều nhất trong mẫu số liệu được gọi là mốt của số liệu, kí hiệu là M0.
Câu 25:
Hàm số bậc hai có bảng biến thiên như hình vẽ có tọa độ điểm đỉnh là
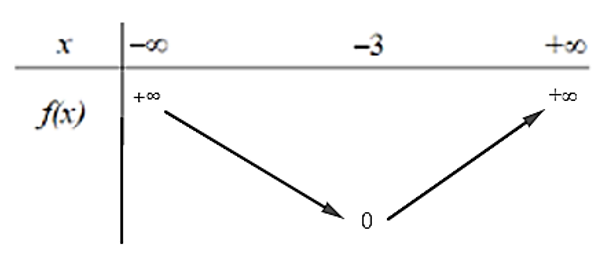
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Dựa vào bảng biến thiên ta có điểm đỉnh I có tọa độ I(– 3; 0).
Câu 26:
Cho điểm I là trung điểm của đoạn thẳng AB. Hỏi đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì I là trung điểm của đoạn thẳng AB nên ta có: .
Câu 27:
Tìm m để hàm số y = (2m – 3)x + m + 1 đồng biến trên R.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Để hàm số đã cho đồng biến trên ℝ thì 2m – 3 > 0 ⇔ m > .
Câu 28:
Cho hình thoi ABCD có cạnh bằng a và . Độ dài bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là B
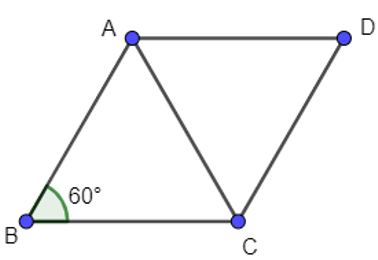
Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B mà . Do đó tam giác ABC đều
Suy ra AB = BC = AC = a.
Ta có:
.
Câu 29:
Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
+) Vì ABCD là hình vuông nên AC ⊥ BD hay OA ⊥ OB nên . Do đó A đúng.
+) Ta có:
Mà (tính chất hình vuông) nên . Do đó B đúng.
+) Ta có: . Do đó C đúng.
+) . Do đó D sai.
Câu 30:
Cho hàm số y = f(x) có bảng biến thiên như sau. Hàm số đã cho đồng biến trên khoảng:
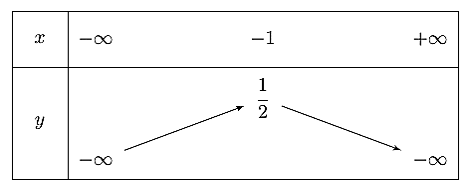
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hàm số đồng biến (đi lên) trên khoảng .
Câu 31:
Chu vi của hình chữ nhật có chiều rộng là x = 3,456 ± 0,01 và chiều dài là y = 12,732 ± 0,015 và ước lượng sai số tuyệt đối mắc phải là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: 3,446 ≤ x ≤ 3,466 và 12,717 ≤ y ≤ 12,747
Khi đó chu vi C = 2(x + y) của hình chữ nhật nằm trong khoảng: 32,326 ≤ C ≤ 32,426
Suy ra 32,376 – 0,05 ≤ C ≤ 32,376 + 0,05 hay C = 32,376 ± 0,05.
Ta có độ chính xác là d = 0,05
Suy ra sai số tuyệt đối của C là: ∆C ≤ 0,05.
Câu 32:
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng ở vị trí C. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 25° và 42°. Biết khoảng cách giữa hai vị trí A và B là 80 m. Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
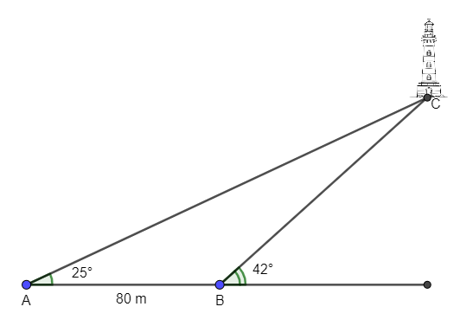
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Kẻ CH vuông góc với bờ AB.
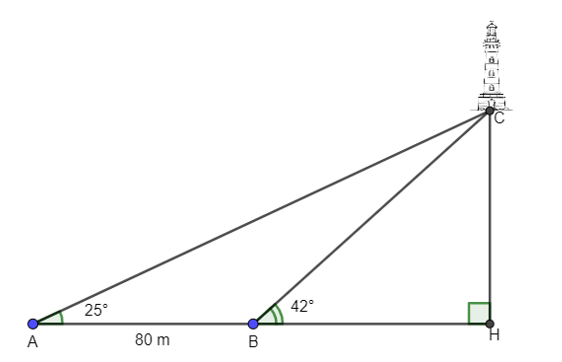
Xét tam giác ABC, có:
(tính chất góc ngoài của tam giác)
Áp dụng định lí sin trong tam giác ABC, ta được:
.
Xét tam giác CHB vuông tại H, có:
.
Vậy khoảng cách từ ngọn hải đăng tới bờ là khoảng 78 m.
Câu 33:
Kết quả điều tra số con của 30 hộ gia đình thuộc một thôn được ghi lại trong bảng sau:

Số trung vị của dãy số liệu trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có bảng tần số sau:
|
Số con (x) |
0 |
1 |
2 |
3 |
4 |
|
Tần số (n) |
2 |
4 |
17 |
5 |
2 |
Dựa vào bảng tần số trên ta có số trung vị của dãy số liệu là trung bình cộng của số liệu thứ 15 và số liệu thứ 16 là: Q2 = .
Câu 34:
Biểu đồ dưới đây thể hiện diện tích lúa cả năm của hai tỉnh An Giang và Kiên Giang từ năm 2010 đến năm 2019 (đơn vị: nghìn hecta):
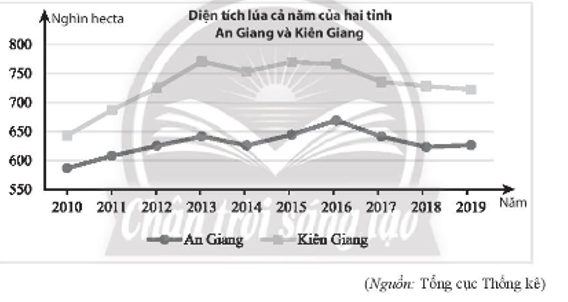
Trong khoảng từ năm 2010 đến 2013 năm mà diện tích lúa tỉnh Kiên Giang gần gấp 1,2 lần diện tích lúa của tỉnh An Giang nhất là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Năm 2010: Diện tích lúa của Kiên Giang là 640 (hecta), của An Giang là 590 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 640 : 590 ≈ 1,08 (lần) diện tích lúa của An Giang.
Năm 2011: Diện tích lúa của Kiên Giang là 690 (hecta), của An Giang là 610 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 690 : 610 ≈ 1,13 (lần) diện tích lúa của An Giang.
Năm 2012: Diện tích lúa của Kiên Giang là 720 (hecta), của An Giang là 620 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 720 : 620 ≈ 1,16 (lần) diện tích lúa của An Giang.
Năm 2013: Diện tích lúa của Kiên Giang là 760 (hecta), của An Giang là 649 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 760 : 649 ≈ 1,17 (lần) diện tích lúa của An Giang.
Câu 35:
Cho tam giác ABC có các góc . Tỉ số bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABC, có:
Áp dụng định lí sin trong tam giác ta được:
.
Câu 36:
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua một chiếc là 27 triệu đồng và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải bán với giá bao nhiêu sau khi giảm giá để lợi nhuận thu được là cao nhất.
 Xem đáp án
Xem đáp án
Gọi số tiền mà doanh nghiệp A dự định giảm giá là x ( triệu đồng) (0 ≤ x ≤ 4).
Tiền lãi khi bán được một xe là: 31 – x – 27 = 4 – x (triệu đồng).
Số lượng xe bán được khi đã giảm giá là: 600 + 200x (xe).
Lợi nhuận cửa hàng thu được là: (600 + 200x)(4 – x) = – 200x2 + 200x + 2 400 (triệu đồng).
Xét hàm số bậc hai y = – 200x2 + 200x + 2 400, có:
Đỉnh I có tọa độ: xI = ; yS = .
Hay
Ta có bảng biến thiên:
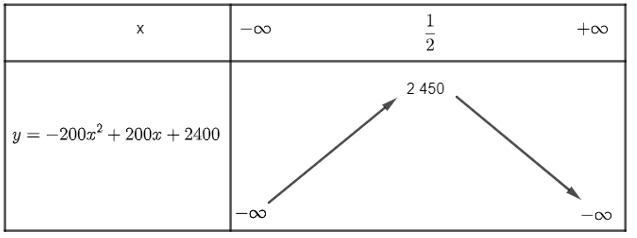
Dựa vào bảng biến thiên ta thấy, hàm số đạt giá trị lớn nhất là 2 450 khi x = .
Vậy doanh nghiệp phải bán với giá 30,5 triệu đồng để lợi nhuận thu được là cao nhất.
Câu 37:
Cho tam giác ABC có G là trọng tâm. Gọi D và E lần lượt là các điểm thỏa mãn đẳng thức .
a) Phân tích vectơ theo hai vectơ và .
 Xem đáp án
Xem đáp án
a) Gọi M là trung điểm của BC
Xét tam giác ABC, có:
.
Cho tam giác ABC có G là trọng tâm. Gọi D và E lần lượt là các điểm thỏa mãn đẳng thức .
a) Phân tích vectơ theo hai vectơ và .
Câu 38:
b) Tìm x để ba điểm D, G, E thẳng hàng. Với giá trị tìm được của x, hãy tính tỉ số .
 Xem đáp án
Xem đáp án
b) Ta có: .
Để D, G, E thẳng hàng thì tồn tại số thực k thỏa mãn:
.
Vậy và khi đó .
Câu 39:
Người ta tiến hành phỏng vấn một số người về chất lượng của một sản phẩm mới, người điều tra yêu cầu cho điểm sản phẩm (thang điểm 100) kết quả như sau:
|
80 |
65 |
51 |
58 |
77 |
12 |
75 |
58 |
|
73 |
79 |
42 |
62 |
84 |
56 |
51 |
82 |
a) Tìm phương sai và độ lệch chuẩn. Nhận xét về các kết quả nhận được.
 Xem đáp án
Xem đáp án
Ta có bảng tần số sau:
|
Điểm |
12 |
42 |
51 |
56 |
58 |
62 |
65 |
73 |
75 |
77 |
79 |
80 |
82 |
84 |
|
Tần số |
1 |
1 |
2 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Số trung bình cộng:
Phương sai:
≈ 326.
Độ lệch chuẩn:
.
Nhận xét: Mức độ chênh lệch giữa các điểm là khá lớn.
Câu 40:
b) Tìm giá trị bất thường.
 Xem đáp án
Xem đáp án
b) Dãy số liệu có tất cả 16 số liệu, nên số trung vị là trung bình cộng của dãy số liệu ở vị trí 8 và vị trí thứ 9 ta được: .
Nửa số liệu bên trái gồm: 12; 42; 51; 51; 56; 58; 58; 62 gồm 8 giá trị. Do đó tứ phân vị thứ nhất là .
Nửa số liệu bên trái gồm: 65; 73; 75; 77; 79; 80; 82; 84 gồm 8 giá trị. Do đó tứ phân vị thứ ba là .
Suy ra khoảng tứ phân vị là: ∆Q = Q3 – Q1 = 78 – 53,5 ≈ 24,5.
Ta có: Q3 + 1,5.∆Q = 114,75 và Q1 – 1,5.∆Q = 16,75.
Ta thấy 12 < 16,75 nên 12 là giá trị ngoại lệ.
