5 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 3. Bất phương trình bậc nhất hai ẩn (Vận dụng) có đáp án

Trắc nghiệm Toán 10 Bài 3. Bất phương trình bậc nhất hai ẩn (phần 2) có đáp án

Trắc nghiệm Toán 10 Bài 3. Bất phương trình bậc nhất hai ẩn (Vận dụng) có đáp án

906 lượt thi
5 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình ax + by > c. Tính giá trị của biểu thức P = a² + b² – 2c ?

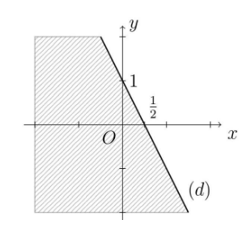
Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm (ảnh 1)

A. P = 3;

B. P = 5;

C. P = 7;

D. P = 4.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:

y = a’x + b’. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là $(\frac{1}{2}; 0)$ và (0; 1). Ta có hệ phương trình

$\{\begin{cases} 0 = \frac{1}{2} . a' + b' \\ 1 = a' .0 + b' \end{cases} \Leftrightarrow \{\begin{cases} a' = - 2 \\ b' = 1 \end{cases} \Rightarrow$ y = – 2x + 1

Vậy đường thẳng có phương trình 2x + y = 1.

Xét điểm O(0; 0), có: 2.0 + 0 = 0 < 1.

Vì O(0; 0) không thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2x + y > 1

Suy ra: a = 2; b = 1; c = 1

⇒ P = a² + b² – 2c = 2² + 1² – 2.1 = 3.

Vậy P = 3.

Câu 2:

Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình (a – 1)x + (2b + 3)y > – 2. Giá trị của a, b là?

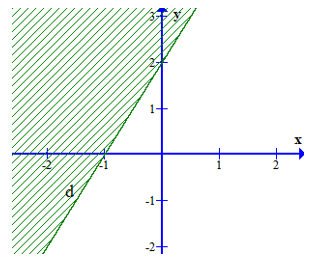
Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây (ảnh 1)

A. a = – 2; b = 1;

B. a = 2; b = – 1;

C. a = 3; b = – 2;

D. a = – 1; b = – 1.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:

y = a’x + b’. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (– 1; 0) và (0; 2). Ta có hệ phương trình

$\{\begin{cases} 0 = - 1. a' + b' \\ 2 = a' .0 + b' \end{cases} \Leftrightarrow \{\begin{cases} a' = 2 \\ b' = 2 \end{cases} \Rightarrow$ y = 2x + 2

Suy ra đường thẳng có phương trình – 2x + y = 2.

Xét điểm O(0; 0), có: – 2.0 + 0 = 0 < 2.

Vì O(0; 0) thuộc miền nghiệm của bất phương trình. Do đó phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình – 2x + y < 2 2x – y > – 2

Ta có a – 1 = 2 a = 3; 2b + 3 = – 1 b = – 2

Vậy a = 3 và b = – 2.

Câu 3:

Phần nửa mặt phẳng tô đậm (không kể đường thẳng ∆) trong hình vẽ dưới đây biểu diễn miền nghiệm của bất phương trình ax + by > c. Hệ số a, c là nghiệm của hệ phương trình?

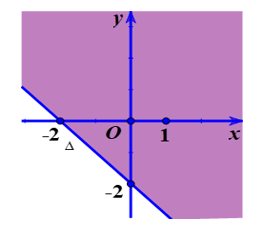
Phần nửa mặt phẳng tô đậm (không kể đường thẳng tam giác) trong hình vẽ dưới đây biểu diễn miền nghiệm (ảnh 1)

A. $\{\begin{cases} 2 a + 5 c = - 8 \\ a - c = 3 \end{cases}$

B. $\{\begin{cases} 2 a + c = 0 \\ a - c = - 1 \end{cases}$

C. $\{\begin{cases} 2 a + 5 c = 12 \\ a - c = - 1 \end{cases}$

D. $\{\begin{cases} 2 a + c = 4 \\ a + c = 3 \end{cases}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Giả sử đường thẳng (∆) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:

y = a’x + b’. Dễ dàng nhận thấy đường thẳng (∆) đi qua hai điểm có tọa độ là (– 2; 0) và (0; – 2). Ta có hệ phương trình

$\{\begin{cases} 0 = a' . (- 2) + b' \\ - 2 = a' .0 + b' \end{cases} \Leftrightarrow \{\begin{cases} a' = - 1 \\ b' = - 2 \end{cases} \Rightarrow$ y = – x – 2

Vậy đường thẳng có phương trình x + y = – 2

Xét điểm O(0; 0), có: 0 + 0 = 0 > – 2.

Vì O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy phần tô đậm biểu diễn miền nghiệm của bất phương trình x + y > – 2 (không kề đường thẳng ∆)

Ta có a = 1; b = 1; c = – 2

Xét hệ phương trình A: $\{\begin{cases} 2 a + 5 c = - 8 \\ a - c = 3 \end{cases} \Leftrightarrow \Leftrightarrow \{\begin{cases} a = 1 \\ c = - 2 \end{cases}$ .

Xét hệ phương trình B: $\{\begin{cases} 2 a + c = 0 \\ a - c = - 1 \end{cases} \Leftrightarrow \{\begin{cases} a = - \frac{1}{3} \\ c = \frac{2}{3} \end{cases}$

Xét hệ phương trình C: $\{\begin{cases} 2 a + 5 c = 12 \\ a - c = - 1 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ c = 2 \end{cases}$

Xét hệ phương trình D: $\{\begin{cases} 2 a + c = 4 \\ a + c = 3 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ c = 2 \end{cases}$

Vậy chọn đáp án A.

Câu 4:

Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình ax + by ≥ c. Kết luận nào sau đây đúng?

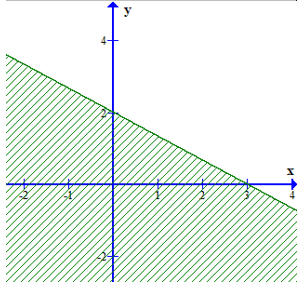
Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) ở hình dưới đây là miền nghiệm của (ảnh 1)

A. a > b > c;

B. a < b < c;

C. b < a < c;

D. a < c < b.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:

y = a’x + b’. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (3; 0) và (0; 2). Ta có hệ phương trình

$\{\begin{cases} 0 = 3. a' + b' \\ 2 = a' .0 + b' \end{cases} \Leftrightarrow \{\begin{cases} a' = - \frac{2}{3} \\ b' = 2 \end{cases}$ $\Leftrightarrow$ y = x + 2 ⇔ 2x + 3y = 6

Suy ra đường thẳng d có phương trình 2x + 3y = 6.

Xét điểm O(0; 0), ta có: 2.0 + 3.0 = 0 < 6.

Vì O(0; 0) không thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2x + 3y ≥ 6

Ta có a = 2; b = 3; c = 6

Suy ra a < b < c.

Vậy chọn đáp án B.

Câu 5:

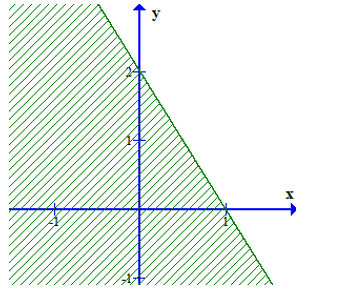
Có bao nhiêu giá trị của m để phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình (m² – 3m + 2)x – y < – 2.

Có bao nhiêu giá trị của m để phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) (ảnh 1)

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:

y = ax + b. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (1; 0) và (0; 2). Ta có hệ phương trình

y = – 2x + 2

Vậy đường thẳng có phương trình 2x + y = 2.

Xét điểm O(0; 0), ta có: 2.0 + 0 = 0 < 2.

Vì O(0; 0) không thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2x + y > 2 – 2x – y < – 2

Suy ra: m² – 3m + 2 = – 2 ⇔ m² – 3m + 4 = 0 có ∆ = (– 3)² – 4.4 = – 7 < 0. Do đó phương trình vô nghiệm.

Vậy không có giá trị của m thoả mãn

Bắt đầu thi ngay