5 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài ôn tập cuối chương 1 (Vận dụng) có đáp án

Trắc nghiệm Toán 10 Bài ôn tập cuối chương 1 (phần 2) có đáp án

Trắc nghiệm Toán 10 Bài ôn tập cuối chương 1 (Vận dụng) có đáp án

991 lượt thi
5 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho A = {x ∈ ℝ | |x – m| ≤ 25}; B = {x ∈ ℝ | |x| ≥ 2020}.

Có bao nhiêu giá trị nguyên m thỏa mãn A ∩ B = ∅.

A. 3987;

B. 3988;

C. 3989;

D. 2020.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có:

A = {x ∈ ℝ | |x – m| ≤ 25} ⟹ A = [m – 25; m + 25]

B = {x ∈ ℝ | |x| ≥ 2020} ⟹ B = (-∞; -2020] ∪ [2020; +∞)

Để A ∩ B = ∅ thì -2020 < m – 25 và m + 25 < 2020 (1)

Khi đó (1) ⟺ $\{\begin{matrix} m - 25 > - 2020 \\ m + 25 < 2020 \end{matrix} \Leftrightarrow \{\begin{matrix} m > - 1995 \\ m < 1995 \end{matrix}$ ⟹ -1995 < m < 1995.

Vậy có 3989 giá trị nguyên m thỏa mãn.

Câu 2:

Cho mệnh đề chứa biến P(x) = {x ∈ ℤ : |x² – 2x – 3| = x² + |2x + 3|}. Trong đoạn [-2020; 2021] có bao nhiêu giá trị của x để mệnh đề chứa biến P(x) là mệnh đề đúng?

A. 2020;

B. 2021;

C. 2022;

C. 2023

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Số giá trị nguyên để mệnh đề P(x) là mệnh đề đúng chính là số nghiệm nguyên của phương trình |x² – 2x – 3| = x² + |2x + 3| (1).

+ Nếu x ≥ $- \frac{3}{2}$ thì ta có:

(1) ⟺ |x² – 2x – 3| = x² + |2x + 3| ⇔ $[\begin{matrix} x^{2} - 2 x - 3 = x^{2} + 2 x + 3 \\ - x^{2} + 2 x + 3 = x^{2} + 2 x + 3 \end{matrix} \Leftrightarrow [\begin{matrix} x = - \frac{3}{2} \\ x = 0 \end{matrix}$ .Mà x ∈ ℤ và x ∈ [-2020; 2021] nên x = 0 thỏa mãn.

+ Nếu x < $- \frac{3}{2}$ thì ta có (1) ⟺ |x² – 2x – 3| = x² – 2x – 3. Sử dụng định nghĩa giá trị tuyệt đối, kết hợp với điều kiện, ta có nghiệm của (1) trong trường hợp này:

(1) ⇔ $\{\begin{matrix} x^{2} - 2 x - 3 \geq 0 \\ x < - \frac{3}{2} \end{matrix} \Leftrightarrow \{\begin{matrix} [\begin{matrix} x \leq - 1 \\ x \geq 3 \end{matrix} \\ x < - \frac{3}{2} \end{matrix} \Leftrightarrow x < - \frac{3}{2}$

Mà x ∈ [-2020;2021] nên x ∈ {-2; -3; …; -2020}.

Do đó tập nghiệm của phương trình là S = {0; -2; -3; …; -2020}.

Vậy có 2020 số nguyên thỏa mãn yêu cầu bài toán.

Câu 3:

Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?

A. 20;

B. 45;

C. 38;

D. 21.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

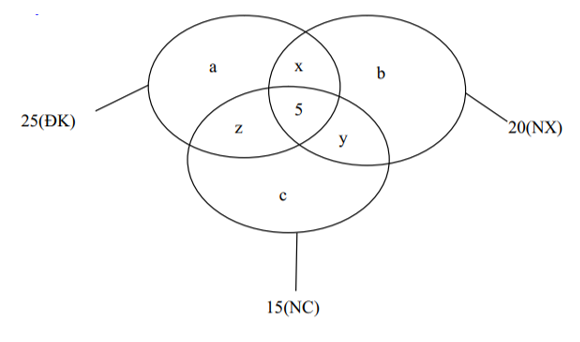
Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền (ảnh 1)

Gọi a, b, c theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
x là số học sinh chỉ thi hai môn điền kinh và nhảy xa.
y là số học sinh chỉ thi hai môn nhảy xa và nhảy cao.
z là số học sinh chỉ thi hai môn điền kinh và nhảy cao.
Số em thi ít nhất một môn là: 45 – 7 = 38
Dựa vào biểu đồ ven ta có hệ phương trình sau:

$\{\begin{matrix} a + x + z + 5 = 25 (1) \\ b + x + y + 5 = 20 (2) \\ c + y + z + 5 = 15 (3) \\ x + y + z + a + b + c + 5 = 38 (4) \end{matrix}$

Cộng vế với vế của (1), (2), (3) ta có: a + b + c + 2(x + y + z) + 15 = 60 (5)

Từ (4) và (5) ta có: a + b + c + 2(38 – 5 – a – b – c) + 15 = 60

⟺ a + b + c = 21.

Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.

Câu 4:

Cho hai tập hợp P = [3m – 6; 4] và Q = (-2; m + 1), m ∈ ℝ. Tìm m để

P\Q = ∅.

A. 3 ≤ m < $\frac{10}{3}$ ;

B. 3 < m <

\frac{10}{3}

;

C. m ≥ 3;

\frac{4}{3}

< m ≤ 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Vì P, Q là hai tập hợp khác rỗng nên ta có điều kiện:

$\{\begin{matrix} 3 m - 6 \leq 4 \\ m + 1 > - 2 \end{matrix} \Leftrightarrow \{\begin{matrix} m \leq \frac{10}{3} \\ m > - 3 \end{matrix}$ $\Leftrightarrow$ -3 < m ≤ $\frac{10}{3}$

Để P\Q = ∅ ⟺ P ⊂ Q

⟺ $\{\begin{matrix} 3 m - 6 > - 2 \\ m + 1 \geq 4 \end{matrix} \Leftrightarrow \{\begin{matrix} m > \frac{4}{3} \\ m \geq 3 \end{matrix}$ m ≥ 3

Kết hợp với điều kiện ta có 3 ≤ m ≤ $\frac{10}{3}$ .

Câu 5:

Mệnh đề nào sau đây đúng?

A. "∀n ∈ ℕ, n(n + 1) là số chính phương";

B. "∀n ∈ ℕ, n(n + 1) là số lẻ";

C. "∃n ∈ ℕ, n(n + 1)(n + 2) là số lẻ";

D. "∀n ∈ ℕ, n(n + 1)(n + 2) chia hết cho 6".

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có:

+ Với n = 1 ⇒ n(n + 1) = 2 không phải là số chính phương ⇒ A sai.

+ Với n = 1 ⇒ n(n + 1) = 2 là số chẵn ⇒ B sai.

Đặt P = n(n + 1)(n + 2)

TH1: n chẵn ⇒ P chẵn

TH2: n lẻ ⇒ (n + 1) chẵn ⇒ P chẵn

Vậy P chẵn ∀n ∈ ℕ ⇒ C sai.

Ta có một số chia hết cho 6 khi và chỉ khi số đó chia hết cho cả 2 và 3.

⟹ P ⋮ 6 ⟺ $\{\begin{matrix} P ⋮ 2 (*) \\ P ⋮ 3 (* *) \end{matrix}$

(*) Ở trên ta đã chứng minh P luôn chẵn ⇒ P ⋮ 2

(**) P ⋮ 3

TH1: n ⋮ 3 ⇒ P ⋮ 3

TH2: n chia 3 dư 1 ⇒ (n + 2) ⋮ 3 ⇒ P ⋮ 3

TH3: n chia 3 dư 2 ⇒ (n + 1) ⋮ 3 ⇒ P ⋮ 3

Vậy P ⋮ 3, ∀n ∈ ℕ.

⇒ P ⋮ 6.

Do đó mệnh đề ở câu D đúng.

Bắt đầu thi ngay