Trắc nghiệm Toán 10 Bài ôn tập cuối chương 1 (Thông hiểu) có đáp án
-
1049 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong các tập hợp sau đây, tập hợp nào là tập hợp rỗng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
A. Ta có:
x2 – 9 = 0 ⟺ x2 = 9 ⟺
Vì x ∈ ℤ nên hai nghiệm trên đều thỏa mãn.
⟹ A = {-3; 3}.
B. Ta có:
x2 – 6 = 0 ⟺ x2 = 6 ⟺
Vì x ∈ ℝ nên hai nghiệm trên đều thỏa mãn.
⟹ B = { }.
C. Ta có:
Phương trình x2 + 1 = 0 vô nghiệm.
⟹ Tập hợp C không có phần tử nào thỏa mãn.
⟹ C = ∅.
D. Ta có:
x2 – 4x + 3 = 0 ⟺ .
Vì x ∈ ℝ nên hai nghiệm trên đều thỏa mãn.
⟹ B = {1; 3}.
Vậy C là tập hợp rỗng.
Câu 2:
Tập hợp X = {x ∈ ℤ | 2 < 2x – 4 < 10} bằng tập hợp nào sau đây?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
2 < 2x – 4 < 10
⟺ 2 + 4 < 2x < 10 + 4
⟺ 6 < 2x < 14
⟺ 3 < x < 7.
Vì x ∈ ℤ nên x nhận các giá trị là 4; 5; 6.
⟹ X = {4; 5; 6}.
Đối chiếu các đáp án trên ta thấy các phần tử trong tập hợp X cũng là các phần tử trong tập hợp D nên A = D.
Câu 3:
Cho mệnh đề chứa biến P(x): x ∈ ℝ: x2 + 2 > 12. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét bất phương trình (*): x2 + 2 > 12.
A. Thay x = 2 vào phương trình (*) ta có: 22 + 2 = 6 > 12 (vô lý)
Suy ra mệnh đề trên sai.
B. Thay x = 1 vào phương trình (*) ta có: 12 + 2 = 3 > 12 (vô lý).
Suy ra mệnh đề trên sai.
C. Thay x = 3 vào phương trình (*) ta có: 32 + 2 = 11 > 12 (vô lý).
Suy ra mệnh đề trên sai.
D. Thay x = 4 vào phương trình (*) ta có: 42 + 2 = 18 > 12 (đúng).
Suy ra mệnh đề trên đúng.
Câu 4:
Mệnh đề phủ định của mệnh đề “Có ít nhất một số thực x thỏa mãn điều kiện bình phương của nó là 1 số không dương” là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Theo giả thiết, ta có mệnh đề P: "∃x ∈ ℝ: x2 ≤ 0".
Ta có:
- Phủ định của ∃ phải là ∀.
- Phủ định của quan hệ ≤ là quan hệ >.
Vậy mệnh đề phủ định của mệnh đề P là: ∀x ∈ ℝ: x2 > 0.
Câu 5:
Cho tập hợp B = {x ∈ ℕ| 3 < 2x – 1 < m}.
Tìm giá trị của m để B là tập hợp rỗng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Xét bất phương trình 3 < 2x – 1 < m (*).
A. Thay m = 7 vào bất phương trình (*) ta có:
3 < 2x – 1 < 7
⟺ 3 + 1 < 2x < 7 + 1
⟺ 4 < 2x < 8
⟺ 2 < x < 4.
Vì x ∈ ℕ nên ta nhận giá trị x = 3.
⟹ m = 7 thì A = {3}.
B. Thay m = 5 vào bất phương trình (*) ta có:
3 < 2x – 1 < 5
⟺ 3 + 1 < 2x < 5 + 1
⟺ 4 < 2x < 6
⟺ 2 < x < 3.
Vì x ∈ ℕ nên không có giá trị của x nào thỏa mãn.
⟹ m = 5 thì B = ∅.
C. Thay m = 9 vào bất phương trình (*) ta có:
3 < 2x – 1 < 9
⟺ 3 + 1 < 2x < 9 + 1
⟺ 4 < 2x < 10
⟺ 2 < x < 5.
Vì x ∈ ℕ nên ta nhận giá trị x = 3 và x = 4.
⟹ m = 7 thì A = {3; 4}.
D. Thay m = 8 vào bất phương trình (*) ta có:
3 < 2x – 1 < 8
⟺ 3 + 1 < 2x < 8 + 1
⟺ 4 < 2x < 9
⟺ 2 < x < .
Vì x ∈ ℕ nên ta nhận giá trị x = 3 và x = 4.
⟹ m = 7 thì A = {3; 4}.
Vậy m = 5 thì B là tập hợp rỗng.
Câu 6:
Câu nào sau đây không phải là mệnh đề chứa biến?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
A. Câu trên là mệnh đề chứa biến vì câu trên phụ thuộc vào biến x.
B. Câu B là mệnh đề vì đó là câu khẳng định tính đúng sai.
Nên câu trên không phải là mệnh đề chứa biến.
C. Câu trên là mệnh đề chứa biến vì câu trên phụ thuộc vào biến và ta có tập D của các biến x để câu trên đúng hoặc sai.
D. Câu trên là mệnh đề chứa biến vì câu trên phụ thuộc vào biến và ta có tập D của các biến x để câu trên đúng hoặc sai.
Câu 7:
Trong các tập hợp sau, tập hợp nào không phải là tập hợp rỗng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
A. Ta có:
Phương trình x2 + x + 3 = 0 vô nghiệm.
⟹ Tập hợp A không có phần tử nào thỏa mãn.
⟹ C = ∅.
B. Ta có:
x2 + 6x + 5 = 0 ⟺
Vì x ∈ ℕ* nên không có phần tử nào thỏa mãn tập hợp trên.
⟹ B = ∅.
C. Ta có:
x(x2 – 5) = 0 ⟺ .
Vì x ∈ ℕ nên không có phần tử nào thỏa mãn tập hợp trên.
⟹ C = ∅.
D. Ta có:
x2 – 9x + 20 = 0 ⟺ .
Vì x ∈ ℕ* nên hai nghiệm x = 4 và x = 5 đều thỏa mãn.
Do đó tập hợp D có hai phần tử.
⟹ D = {4; 5}.
Vậy chỉ có tập hợp D không phải là tập hợp rỗng.
Câu 8:
Cho mệnh đề sau:
Cho tứ giác ABCD, ta có các mệnh đề sau:
P: “x là số nguyên dương”.
Q: “x2 là số nguyên dương”.
Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
A. Xét mệnh đề P ⟹ Q: “Nếu x là số nguyên dương thì x2 là số nguyên dương”.
Mệnh đề này đúng vì bình phương của một số nguyên dương là một số nguyên dương. (1)
Xét mệnh đề đảo Q ⇒ P: “Nếu x2 là số nguyên dương thì x là số nguyên dương”.
Mệnh đề này sai do nếu x2 là số nguyên dương thì x có thể là số thực dương hoặc số thực âm. (2)
Từ (1) và (2) nên mệnh đề ở đây A sai.
B. Mệnh đề Q ⇒ P được phát biểu như sau: “Nếu x2 là số nguyên dương thì x là số nguyên dương”.
Mệnh đề này sai do nếu x2 là số nguyên dương thì x có thể là số thực dương hoặc số thực âm.
C. Ta có mệnh đề : “x2 không phải là số nguyên dương”.
Mệnh đề P ⇒ được phát biểu như sau: “Nếu x là số nguyên dương thì x2 không phải là số nguyên dương”.
Vì với x nguyên dương thì x2 luôn luôn dương nên mệnh đề trên sai.
D. Mệnh đề P ⇒ Q được phát biểu như sau: “Nếu x là số nguyên dương thì x2 là số nguyên dương”.
Mệnh đề này đúng vì bình phương của một số nguyên dương là một số nguyên dương.
Câu 9:
Lớp 10B1 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10B1 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta dùng biểu đồ Ven để giải:
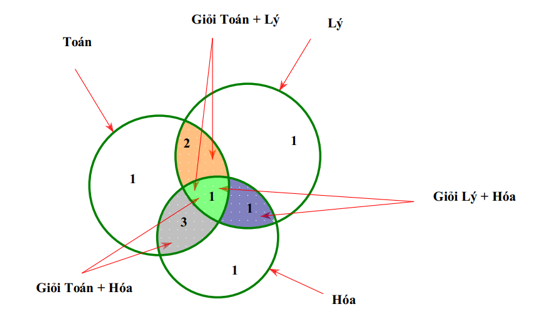
Nhìn vào biểu đồ, số học sinh giỏi ít nhất 1 trong 3 môn là: 1+ 2 + 1 + 3 + 1 + 1 + 1 = 10.
Câu 10:
Mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Mệnh đề kéo theo “ P suy ra Q” chỉ sai khi P đúng Q sai.
A. Xét mệnh đề “Nếu (-3) > (-2) thì (-3)2 > (-2)2” có mệnh đề P : “(-3) > (-2)” là mệnh đề sai, mệnh đề Q : “(-3)2 > (-2)2” là mệnh đề đúng. Do đó mệnh đề kéo theo P ⇒ Q là mệnh đề đúng.
B. Xét mệnh đề “Nếu 3 là số lẻ thì 3 chia hết cho 2”;
Mệnh đề “3 là số lẻ” là đúng, tuy nhiên mệnh đề “3 chia hết cho 2” sai.
Theo lý thuyết “Mệnh đề P ⇒ Q sai khi P đúng và Q sai”
Nên mệnh đề ở câu B sai.
C. Xét mệnh đề “Nếu 15 chia hết cho 9 thì 18 chia hết cho 3”
Mệnh đề P: “15 chia hết cho 9” là sai.
Mệnh đề Q: “18 chia hết cho 3” là mệnh đề đúng.
Do đó mệnh đề C là mệnh đề đúng.
D. Xét mệnh đề: “Nếu 3 chia hết cho 1 và chính nó thì 3 là số nguyên tố”.
Mệnh đề P: “3 chia hết cho 1 và chính nó” là mệnh đề đúng;
Mệnh đề Q: “3 là số nguyên tố” là mệnh đề đúng.
Do đó mệnh đề P ⇒ Q đúng.
Câu 11:
Tập hợp C = {x ∈ ℤ | (x2 – 5x + 4)(x2 x + 3) = 0} có bao nhiêu phần tử?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
(x2 – 5x + 4)(x2 x + 3) = 0
⟺
Vì x ∈ ℤ nên ta loại nghiệm .
⟹ C = {1; 2; 4}.
⟹ n(C) = 3.
Câu 12:
Cho ba tập hợp sau:
A = {m + 1; 2}
B = {1; n – 3}
C = {t; 2}
Hỏi m, n, t nhận giá trị nào sau đây thì A = B = C?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta thấy tập hợp A có 2 phần tử là m + 1 và 2.
Mà tập hợp B có 2 phần tử là 1 và n – 3.
Do đó để A = B thì .
Ta lại có tập hợp C có 2 phần tử là t và 2.
Do đó để B = C thì t = 1.
Vậy để A = B = C thì m = 0, n = 5, t = 1.
Câu 13:
Kí hiệu X là tập hợp tất cả các bạn học sinh x trong lớp 10A1, P(x) là mệnh đề chứa biến “x đạt học sinh giỏi”. Mệnh đề “∃x ∈ X, P(x)” khẳng định rằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có mệnh đề “∃x ∈ X, P(x)” được phát biểu như sau:
“Có một số bạn học lớp 10A1 đạt học sinh giỏi”.
Đối chiếu các đáp án, ta thấy đáp án C là phù hợp nhất.
Câu 14:
Cho mệnh đề sau: “Trong một mặt phẳng, nếu hai đường thẳng cùng song song với đường thẳng thứ 3 thì hai đường thẳng đó song song với nhau”.
Đáp án nào dưới đây là cách viết khác với mệnh đề đã cho?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét mệnh đề “Trong một mặt phẳng, nếu hai đường thẳng cùng song song với đường thẳng thứ 3 thì hai đường thẳng đó song song với nhau” ta có:
P: “Trong một mặt phẳng, hai đường thẳng cùng song song với đường thẳng thứ 3”.
Q: “Hai đường thẳng đó song song với nhau”.
Ta thấy mệnh đề trên có dạng P ⇒ Q có thể được phát biểu dưới dạng điều kiện cần, điều kiện đủ như sau:
+ P là điều kiện đủ để có Q.
+ Q là điều kiện cần để có P.
Do đó định lý đã cho được phát biểu dưới dạng điều kiện cần, điều kiện đủ lần lượt là:
+ Trong một mặt phẳng, hai đường thẳng cùng song song với đường thẳng thứ 3 là điều kiện đủ để hai đường thẳng đó song song với nhau.
+ Trong một mặt phẳng, hai đường thẳng song song với nhau là điều kiện cần để hai đường thẳng đó cùng song song với đường thẳng thứ 3.
Đối chiếu với các đáp án trên, ta thấy mệnh đề ở đáp án D là một cách viết khác của mệnh đề đã cho.
Câu 15:
Cho các tập hợp:
A = {x ∈ ℤ | -4 ≤ x ≤ 5};
B = {x ∈ ℤ | -2 ≤ x ≤ 6};
C = {x ∈ ℤ | 0 ≤ x ≤ 1}.
Xác định tập hợp X = (A ∩ B)\C. Câu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có:
+ Các phần tử của tập hợp A là -4; -3; -2; -1; 0; 1; 2; 3; 4; 5.
⟹ A = {-4; -3; -2; -1; 0; 1; 2; 3; 4; 5}.
+ Các phần tử của tập hợp B là -2; -1; 0; 1; 2; 3; 4; 5; 6.
⟹ B = {-2; -1; 0; 1; 2; 3; 4; 5; 6}.
+ Các phần tử của tập hợp C là 0; 1.
⟹ C = {0; 1}.
- Giao của hai tập hợp A và B là tập hợp các phần tử thuộc tập hợp A cũng thuộc tập hợp B, do đó các phần tử thuộc tập hợp A ∩ B là -2; -1; 0; 1; 2; 3; 4; 5.
⟹ A ∩ B = {-2; -1; 0; 1; 2; 3; 4; 5}.
- Các phần tử thuộc tập hợp A ∩ B mà không thuộc tập hợp C là -2; -1; 2; 3; 4; 5.
⟹ X = (A ∩ B)\C = {-2; -1; 2; 3; 4; 5}.
