7 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 CTST Bài tập cuối chương 9 (Vận dụng) có đáp án

Câu 1:

Viết phương trình tham số của đường thẳng d đi qua M(2; 6) và song song với đường thẳng x + 3y – 10 = 0.

A. $\{\begin{cases} x = 2 + t \\ y = 6 + 3 t \end{cases}$

B. $\{\begin{cases} x = 2 + 3 t \\ y = 6 + t \end{cases}$

C. $\{\begin{cases} x = 5 - t \\ y = 5 + 3 t \end{cases}$

D. $\{\begin{cases} x = 5 + 3 t \\ y = 5 - t \end{cases}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Đường thẳng x + 3y – 10 = 0 có vectơ pháp tuyến là: $\vec{n} = (1; 3)$ .

Do đường thẳng d song song với đường thẳng x + 3y – 10 = 0 nên $\vec{n} = (1; 3)$ cũng là vectơ pháp tuyến của đường thẳng d.

Khi đó đường thẳng d có vectơ chỉ phương là $\vec{u} = (3; - 1)$ .

Đường thẳng d có vectơ chỉ phương $\vec{u} = (3; - 1)$ và đi qua M(2; 6) có phương trình tham số là: $\{\begin{cases} x = 2 + 3 t \\ y = 6 - t \end{cases}$ .

Với t = 1 ta có $\{\begin{cases} x = 2 + 3.1 = 5 \\ y = 6 - 1 = 5 \end{cases}$ , khi đó điểm A(5; 5) thuộc đường thẳng d.

Do đó ta có phương trình tham số của đường thẳng d là $\{\begin{cases} x = 5 + 3 t \\ y = 5 - t \end{cases}$ .

Vậy ta chọn phương án D.

Câu 2:

Đường thẳng d tạo với đường thẳng $∆$ : x + 2y – 6 = 0 một góc 45°. Hệ số góc k của đường thẳng d là:

A. k = $\frac{1}{3}$ hoặc k = – 3;

B. k = $\frac{1}{3}$ hoặc k = 3;

C. k = $- \frac{1}{3}$ hoặc k = – 3;

D. k =

- \frac{1}{3}

hoặc k = 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Đường thẳng D: x + 2y – 6 = 0 có vectơ pháp tuyến là ${\vec{n}}_{Δ} = (1; 2)$ .

Gọi ${\vec{n}}_{d} = (a; b)$ là vectơ pháp tuyến của đường thẳng d.

Khi đó hệ số góc của đường thẳng d là $k = - \frac{a}{b}$ .

Góc giữa hai đường thẳng d và $∆$ là 45° nên ta có:

$cos (d, Δ) = |cos ({\vec{n}}_{d}, {\vec{n}}_{Δ})| = c os45 °$

Hay $\frac{|1. a + 2. b|}{\sqrt{1^{2} + 2^{2}} . \sqrt{a^{2} + b^{2}}} = \frac{1}{\sqrt{2}}$

$\Leftrightarrow \sqrt{5} . \sqrt{a^{2} + b^{2}} = \sqrt{2} . |a + 2 b|$

$\Leftrightarrow$ 5(a² + b²) = 2(a + 2b)²

$\Leftrightarrow$ 5a² + 5b² = 2a² + 8ab + 8b²

$\Leftrightarrow$ 3a² – 8ab – 3b² = 0

$\Leftrightarrow [\begin{array}{l} a = 3 b \\ a = - \frac{1}{3} b \end{array} \Leftrightarrow [\begin{array}{l} \frac{a}{b} = 3 \\ \frac{a}{b} = - \frac{1}{3} \end{array} \Leftrightarrow [\begin{array}{l} k = - \frac{a}{b} = - 3 \\ k = - \frac{a}{b} = \frac{1}{3} \end{array}$ .

Vậy ta chọn phương án A.

Câu 3:

Cho phương trình x² + y² – 2(m + 1)x + 4y – 1 = 0 (1). Với giá trị nào của m thì (1) là phương trình đường tròn có bán kính nhỏ nhất?

A. m = 2;

B. m = – 1;

C. m = 1;

D. m = –2.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có x² + y² – 2(m + 1)x + 4y – 1 = 0 có a = m + 1; b = –2 và c = –1.

Để (1) là phương trình đường tròn thì a² + b² – c > 0

$\Leftrightarrow$ (m + 1)² + (–2)² – (–1) > 0

$\Leftrightarrow$ (m + 1)² + 5 > 0 (luôn đúng với mọi m).

Khi đó bán kính của đường tròn này là $R = \sqrt{a^{2} + b^{2} - c}$

Hay R² = (m + 1)² + 5 ≥ 5, với mọi m.

Dấu “=” xảy ra khi và chỉ khi m + 1 = 0 $\Leftrightarrow$ m = –1.

Vậy đường tròn có bán kính nhỏ nhất bằng $R = \sqrt{5}$ khi m = –1.

Câu 4:

Hai con tàu cùng rời cảng và đi theo hai hướng khác nhau. Chọn hệ trục tọa độ sao cho bến cảng là gốc tọa độ. Khi đó quãng đường đi được và hướng của tàu thứ nhất và thứ hai được biểu thị bởi hai vectơ ${\vec{s}}_{1}, {\vec{s}}_{2}$ như hình dưới đây (độ dài một đơn vị trên trục tương ứng với 100 m trên thực tế).

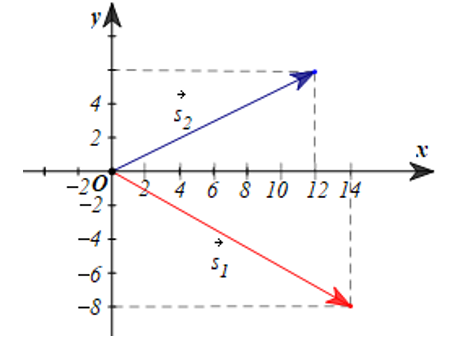
Hai con tàu cùng rời cảng và đi theo hai hướng khác nhau. Chọn hệ trục tọa độ sao (ảnh 1)

Hỏi quãng đường tàu thứ nhất đi được dài hơn tàu thứ hai bao nhiêu mét? Khoảng cách giữa hai tàu là bao nhiêu mét? (kết quả làm tròn đến hàng phần trăm).

A. 347,54 m và 1 216,55 m;

B. 1 216,55 m và 347,50 m;

C. 347,54 m và 2 877,36 m;

D. 2 877,36 m và 347,54 m.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Khoảng cách mà mỗi tàu đi được so với cảng chính là $100 |{\vec{s}}_{1}|$ và $100 |{\vec{s}}_{2}|$ .

Do đó, quãng đường tàu thứ nhất đi được dài hơn tàu thứ hai là hiệu $100 |{\vec{s}}_{1}| - 100 |{\vec{s}}_{2}|$ và khoảng cách giữa hai tàu là $100 |{\vec{s}}_{1} - {\vec{s}}_{2}|$ .

Ta có ${\vec{s}}_{1} = (14; - 8), {\vec{s}}_{2} = (12; 4)$ và ${\vec{s}}_{1} - {\vec{s}}_{2} = (2; - 12)$

Suy ra $|{\vec{s}}_{1}| = \sqrt{14^{2} + {(- 8)}^{2}} = 2 \sqrt{65}$ (m);

$|{\vec{s}}_{2}| = \sqrt{12^{2} + 4^{2}} = 4 \sqrt{10}$ (m);

$|{\vec{s}}_{1} - {\vec{s}}_{2}| = \sqrt{2^{2} + {(- 12)}^{2}} = 2 \sqrt{37}$ (m).

Vậy quãng đường tàu thứ nhất đi được dài hơn tàu thứ hai là:

$100.2 \sqrt{65} - 100.4 \sqrt{10} \approx 347, 54$ (m).

Khoảng cách giữa hai tàu là: $100.2 \sqrt{37} \approx 1 216, 55$ (m).

Vậy ta chọn phương án A.

Câu 5:

Một tòa tháp có mặt cắt hình hypebol có phương trình $\frac{x^{2}}{36} - \frac{y^{2}}{49} = 1$ . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp khoảng:

A. 43,28 m;

B. 22,25 m;

C. 28,31 m;

D. 57,91 m.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

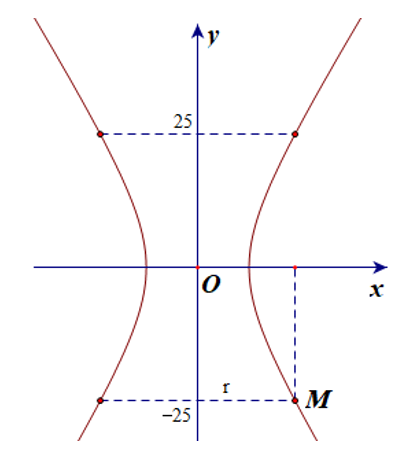
Một tòa tháp có mặt cắt hình hypebol có phương trình x^2/36- y^2/49=1. Biết khoảng (ảnh 1)

Gọi r là bán kính đáy của tháp (r > 0).

Do khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp và do tính đối xứng của hypebol nên ta có hai bán kính của nóc và đáy tháp đều bằng nhau.

Chọn điểm M(r; –25) nằm trên hypebol.

Ta suy ra $\frac{r^{2}}{36} - \frac{{(- 25)}^{2}}{49} = 1$ .

$\Leftrightarrow \frac{r^{2}}{36} = 1 + \frac{{(- 25)}^{2}}{49} = \frac{674}{49}$ .

$\Leftrightarrow r^{2} = \frac{674}{49} .36 = \frac{24264}{49}$ .

Suy ra $r = \frac{6 \sqrt{674}}{7} \approx 22, 25$ (m).

Vậy bán kính đáy của tháp bằng khoảng 22,25 m.

Ta chọn phương án B.

Câu 6:

Một cổng của một trường đại học hình Parabol cao 20 m và bề rộng của cổng tại chân cổng là 20 m. Bề rộng của cổng tại chỗ cách đỉnh cổng 4 m là:

Một cổng của một trường đại học hình Parabol cao 20 m và bề rộng của cổng tại chân (ảnh 1)

A. $2 \sqrt{5}$ m;

B. 2 m;

C. 4 m;

D.

\sqrt{5}

m.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

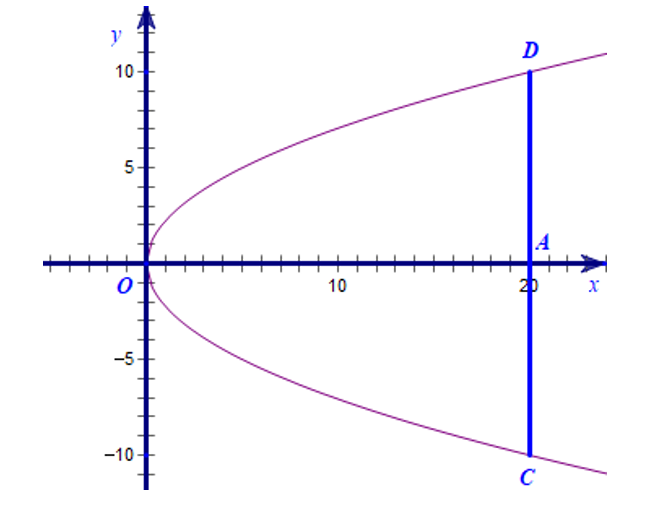
Một cổng của một trường đại học hình Parabol cao 20 m và bề rộng của cổng tại chân (ảnh 2)

Chọn hệ trục tọa độ Oxy như hình vẽ.

Gọi O là đỉnh cổng, A là chân cổng và C, D lần lượt là hai bên trái, phải chân cổng.

Theo bài ra ta có: OA = 20 m, CD = 20 m.

Gọi phương trình Parabol của cổng là y² =2px.

Ta có: AC = AD = CD : 2 = 10 (m)

Do đó điểm D có tung độ là 10.

OA = 20 nên điểm D có hoành độ là 20.

Thay D(20; 10) vào phương trình (P) ta có: $10^{2} = 2 p .20 \Rightarrow p = \frac{5}{2}$

Suy ra y² = 5x.

Thay tọa độ điểm E cách đỉnh 4 m (x = 4) vào (P) ta có:

y² = 5x = 5 . 4 = 20 $\Rightarrow y = \sqrt{20} = 2 \sqrt{5} (m)$

Vậy bề rộng của cổng tại chỗ cách đỉnh 4 m là $2 \sqrt{5}$ m.

Câu 7:

Cho hình vẽ sau:

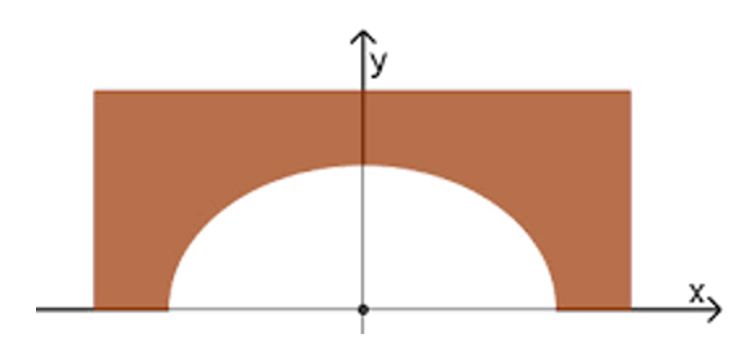
Một cổng hầm hình Elip có dạng như hình trên. Chiều cao của cả hầm là 10 m, chiều rộng là 20 m. Mỗi bên tường dày 2 m và tính từ đỉnh cổng hầm đến đỉnh hầm là 4 m. Phương trình chính tắc của Elip trên là:

A. $\frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$

B. $\frac{x^{2}}{400} + \frac{y^{2}}{100} = 1$

C. $\frac{x^{2}}{64} + \frac{y^{2}}{36} = 1$

D. $\frac{x^{2}}{100} + \frac{y^{2}}{64} = 1$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta thấy chiều cao của cổng hầm là: b = 10 – 4 = 6 (m).

Chiều rộng của cổng hầm là: 2a = 20 – 2.2 = 16 (m).

Suy ra a = 8 (m).

Khi đó ta có phương trình chính tắc của (E) là: $\frac{x^{2}}{64} + \frac{y^{2}}{36} = 1$ .