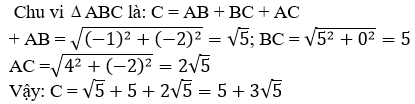25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P3)

Câu 1:

Cho tam giác ABC có a = 3; b = 4 và c = 5. Diện tích S của tam giác trên là:

A. 4

B. 6

C. 8

D. 12

Xem đáp án

Chọn B.

Ta có: Nửa chu vi tam giác là: (3 + 4 + 5) : 2 = 6.

Áp dụng công thức Hê rông:

Câu 2:

Trong mặt phẳng tọa độ; cho 2 điểm A(1; 2) và B(4; 6). Tính khoảng cách giữa hai điểm đó.

A. 4

B. 2

C. 3

D. 5

Xem đáp án

Chọn D.

Câu 3:

Cho tam giác ABC có $S = 10 \sqrt{5}$ , nửa chu vi p = 10. Độ dài bán kính đường tròn nội tiếp của tam giác trên là:

A. 4

B. 3

C. $\sqrt{5}$

D. $\sqrt{3}$

Xem đáp án

Chọn C.

Ta có:

Câu 4:

Cho tam giác ABC có a = 4; c = 5; B = 150⁰. Diện tích của tam giác là:

A. $5 \sqrt{3}$

B. 5

C. 10

D. $10 \sqrt{3}$

Xem đáp án

Chọn B.

Ta có:

Câu 5:

Tam giác ABC có AB = 6 ; AC = 8 và BC = 10. Độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác bằng:

A. 3

B. 6

C. 7

D. 5

Xem đáp án

Chọn D.

Cách 1: Áp dụng công thức đường trung tuyến ta được:

Suy ra m_a= 5

Cách 2: nhận xét đây là tam giác vuông tại A nên m_a= 1/2. BC = 5.

Câu 6:

Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.

A. BM = a.

B. $B M = a \sqrt{2}$

C. $B M = a \sqrt{3}$

D. $B M = \frac{a \sqrt{5}}{2}$

Xem đáp án

Chọn D.

Gọi M là trung điểm của AC suy ra

.

Do tam giác BAM vuông tại A

Câu 7:

Tam giác ABC có AB = 9; AC = 12 và BC = 15cm. Tính độ dài đường trung tuyến AM của tam giác đã cho.

A. 7,5

B. 10.

C. 15.

D. 8,5

Xem đáp án

Chọn A.

Áp dụng hệ thức đường trung tuyến ta được:

Suy ra : m_a= 7,5.

Câu 8:

Tam giác ABC có AB = 5; BC = 7 và CA = 8. Số đo góc A bằng:

A. 45⁰

B. 60⁰

C. 120⁰

D. 30⁰

Xem đáp án

Chọn B.

Theo định lí hàm cosin, ta có

Do đó

Câu 9:

Trong mặt phẳng tọa độ Oxy cho hai vectơ $\vec{u} (3; 4); \vec{v} (- 8; 6)$ . Khẳng định nào sau đây đúng?

A. hai vecto có cùng độ dài.

B. hai vecto cùng phương.

C. Hai vecto vuông góc với nhau.

D. hai vecto ngược hướng.

Xem đáp án

Chọn C.

Ta có

suy ra hai vecto vuông góc với nhau.

Câu 10:

Rút gọn biểu thức sau A = (tanx + cotx)²- ( tanx - cotx)²

A. 3

B. 4

C. 2

D. 1

Xem đáp án

Chọn B.

Ta có: A = (tanx + cotx)²- ( tanx - cotx)²

= tan²x + 2tanx.cot x + cot²x - ( tan²x - 2tanx.cotx + cot²x)

= 4tanx.cotx = 4.

Câu 11:

Đơn giản biểu thức C = (1- sin²x) cot²x + 1 - cot²x.

A. sin²x

B. tan²x

C. cot²x

D. cos²x

Xem đáp án

Chọn A.

Ta có C = (1-sin²x) cot²x + 1 - cot²x.

= (1 - sin²x - 1) cot²x + 1

= -sin²x.cot²x + 1 = -cos²x + 1 = sin²x.

Câu 12:

Câu nào sau đây là phương tích của điểm M(1;2) đối với đường tròn (C) có tâm I(-2;1), bán kính R = 2:

A. 7

B. 6

C. 4

D. 3

Xem đáp án

Chọn B.

Ta có:

Phương tích của điểm M đối với đường tròn (C) tâm I là:

MI²- R²= 10 – 4 = 6

Câu 13:

Một tam giác có ba cạnh là 30; 26; 28. Bán kính đường tròn nội tiếp là:

A. 18

B. 8

C. 6

D. $4 \sqrt{2}$

Xem đáp án

Chọn B.

Ta có nửa chu vi của tam giác đã cho là:

P = (30 + 26 +28) : 2 = 42

Câu 14:

Cho tam giác ABC có a = 4; b = 6; c = 8. Khi đó diện tích của tam giác là:

A. $9 \sqrt{15}$

B. $3 \sqrt{15}$

C. 105

D. $\frac{2}{3} \sqrt{15}$

Xem đáp án

Chọn B.

Nửa chu vi của tam giác là p = (4 + 6 + 8) : 2 = 9

Áp dụng công thức Hê-rông

Suy ra:

Câu 15:

Tam giác với ba cạnh là 5; 12; 13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ?

A. 2

B. $2 \sqrt{2}$

C. 4

D. 3

Xem đáp án

Chọn A.

Ta có nửa chu vi của tam giác đã cho là:

(5 + 12 + 13) : 2 = 15

Mà 5²+ 12²= 13² nên tam giác đã cho là tam giác vuông có diện tích là:

S = 1/2 .5.12 = 30

Mặt khác S = pr nên

Câu 16:

Cho tam giác ABC, biết a = 24; b = 13 và c = 15. Tính góc A?

A. 33⁰34’

B. 112⁰

C. 37⁰28’

D. Tất cả sai

Xem đáp án

Chọn D.

Áp dụng định lí cosin trong tam giác ta có:

Suy ra: A = 117⁰49’

Câu 17:

Tam giác ABC có A = 68⁰12’; B = 34⁰44’, AB =117. Hỏi AC gần với giá trị nào nhất.

A. 68

B. 69

C. 70

D. 92

Xem đáp án

Chọn A

Trong tam giác ABC:

Theo định lí sin trong tam giác ta có:

Câu 18:

Cho tam giác ABC có AB = 10; AC = 4 và góc A bằng 60⁰. Tính chu vi của tam giác.

A. 22,2

B. 22,72

C. 22,61

D. 22,48

Xem đáp án

Chọn B.

Theo định lí côsin ta có

BC²= AB²+ AC²- 2.AB.AC.cos A = 10²+ 4²- 2.10.4.cos 60 = 76

Suy ra BC ≈ 8,72

Suy ra chu vi tam giác là 10 + 4 + 8,72 = 22,72

Câu 19:

Cho tam giác ABC, Tìm mệnh đề đúng.

A. sinA = sin(B - C)

B. sinA = cos( A + B)

C. sinA = cosA + cosB

D. sinA = sin(B + C)

Xem đáp án

Chọn D.

Ta có: A + B + C = 180⁰ ⇒ A = 180⁰ – (B + C)

Khi đó: sinA = sin(180⁰ – (B + C)) = sin(B + C)

Câu 20:

Cho góc x, với cosx = 2/3. Tính giá trị của biểu thức: P = 5sin²x + 2cos²x.

A. 22/9

B. 8/3

C. 33/9

D. 1

Xem đáp án

Chọn C.

Ta có: sin²x + cos²x = 1 ⇒ sin²x = 1 – cos²x = 1 – 4/9 = 5/9

Vậy:

Câu 21:

Tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ , biết $\vec{a} (1; - 2); \vec{b} (- 1; - 3)$

A. 30⁰

B. 45⁰

C. 60⁰

D. 90⁰

Xem đáp án

Chọn B.

Ta có:

Suy ra

Câu 22:

Tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ , biết: $\vec{a} (2; - 2); \vec{b} (2; 2)$

A. 30⁰

B. 45⁰

C. 60⁰

D. 90⁰

Xem đáp án

Chọn D.

Ta có:

Suy ra

Câu 23:

Tìm m để góc giữa 2 vecto $\vec{a} (m; 2)$ và $\vec{b} (2; - 1)$ bằng 180⁰

A. m = -4

B. m = -3

C. m = -2

D. m = 0

Xem đáp án

Chọn A.

Để góc giữa 2 vecto bằng 180⁰ thì 2 vecto ban đầu là ngược hướng

Do đó; m = -4.

Câu 24:

Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2). Hỏi tam giác ABC là tam giác gì?

A. tam giác cân

B. tam giác đều

C. tam giác nhọn

D. tam giác vuông

Xem đáp án

Chọn D.

Ta có:

suy ra

do đó; 2 vecto AB và AC vuông góc với nhau

suy ra tam giác ABC vuông tại A.

Câu 25:

Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2).Tính chu vi tam giác ABC.

A. 5

B. $5 + 2 \sqrt{5}$

C. $5 + 3 \sqrt{5}$

D. Đáp án khác

Xem đáp án

Chọn C.