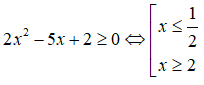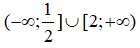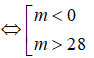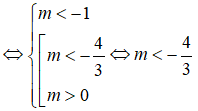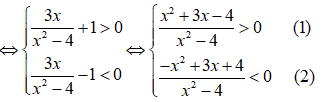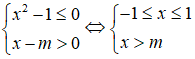8 câu hỏi trắc nghiệm thuộc Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 4)

Top 4 Đề kiểm tra 15 phút Toán 10 Chương 4 Đại Số có đáp án

Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 4)

2854 lượt thi
8 câu hỏi
15 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tập xác định của hàm số $y = \sqrt{2 x^{2} - 5 x + 2}$

A. (- $\infty$ ; $\frac{1}{2}$ ]

B. [2;+ $\infty$ )

C. (- $\infty$ ; $\frac{1}{2}$ ] $\cup$ [2;+ $\infty$ )

D. [ $\frac{1}{2}$ ;2]

Xem đáp án

Đáp án C

Hàm số 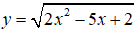xác định khi và chỉ khi:

Vậy tập xác định của hàm số là:

Câu 2:

Các giá trị m để tam thức f(x) = $x^{2}$ - (m + 2)x + 8m + 1 đổi dấu 2 lần là:

A. m ≤ 0 hoặc m ≥ 28

B. m < 0 hoặc m > 28

C. 0 < m < 28

D. m > 0

Xem đáp án

Đáp án: B

Tam thức f(x) = $x^{2}$ - (m + 2)x + 8m + 1 đổi dấu hai lần khi và chỉ khi f(x) có hai nghiệm phân biệt

Ta có: Δ = [-(m + 2) $]^{2}$ - 4.(8m + 1) = $m^{2}$ - 28m

f(x) có hai nghiệm phân biệt khi và chỉ khi

Δ > 0 ⇔ $m^{2}$ - 28m > 0

Câu 3:

Cho bảng xét dấu:

Bảng xét dấu trên là của tam thức bậc hai nào sau đây?

A. f(x) = - $x^{2}$ - x + 6

B. f(x) = $x^{2}$ + x - 6

C. f(x) = - $x^{2}$ + x + 6

D. f(x) = $x^{2}$ - x + 6

Xem đáp án

Đáp án: A

Từ bảng xét dấu ta thấy phương trình f(x) = 0 có 2 nghiệm là -3 và 2. Do đó, ta loại được đáp án C và D

Dựa vào bảng xét dấu, f(x) > 0 trong khoảng (-3;2) do đó hệ số a < 0

Câu 4:

Tìm m để (m + 1) $x^{2}$ + mx + m < 0, ∀x ∈ R?

A. m < -1

B. m > -1

C. m < - $\frac{4}{3}$

D. m > $\frac{4}{3}$

Xem đáp án

Đáp án C

Bất phương trình (m + 1) $x^{2}$ + mx + m < 0, ∀x ∈ R khi và chỉ khi:

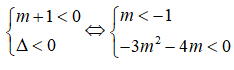
Câu 5:

Tập nghiệm của bất phương trình $|\frac{3 x}{x^{2} - 4}| < 1$ là:

A. (- $\infty$ ;-4) ∪ (-1;1) ∪ (4;+ $\infty$ )

B. (- $\infty$ ;-4)

C. (-1;1)

D. (4;+ $\infty$ )

Xem đáp án

Đáp án A.

Ta có:

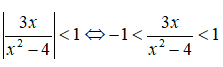
Bảng xét dấu bất phương trình (1):

Dựa vào bảng xét dấu ta thấy tập nghiệm của bất phương trình (1) là: (- $\infty$ ;-4) ∪ (-2;1) ∪ (2;+ $\infty$ )

Bảng xét dấu bất phương trình (2):

Dựa vào bảng xét dấu ta thấy tập nghiệm của bất phương trình (2) là: (- $\infty$ ;-2) ∪ (-1;2) ∪ (4;+ $\infty$ )

Vậy tập nghiệm của hệ bất phương trình là: (- $\infty$ ;-4) ∪ (-1;1) ∪ (4;+ $\infty$ )

Câu 6:

Tập nghiệm của hệ bất phương trình $\{\begin{cases} x^{2} - 4 x + 3 > 0 \\ x^{2} - 6 x + 8 > 0 \end{cases}$ là:

A. (- $\infty$ ;1) ∪ (4;+ $\infty$ )

B. (- $\infty$ ;1) ∪ (3;+ $\infty$ )

C. (- $\infty$ ;2) ∪ (3;+ $\infty$ )

D. (1;4)

Xem đáp án

Đáp án: A

Ta có bảng xét dấu:

Dựa vào bảng xét dấu ta thấy tập nghiệm của bất phương trình là: (- $\infty$ ;1) ∪ (4;+ $\infty$ )

Câu 7:

Hệ bất phương trình $\{\begin{cases} x^{2} - 1 \leq 0 \\ x - m > 0 \end{cases}$ có nghiệm khi:

A. m > 1

B. m < 1

C. m = 1

D. m ≠ 1

Xem đáp án

Đáp án: B

Ta có:

Vậy hệ bất phương trình có nghiệm khi và chỉ khi m < 1

Câu 8:

Xét dấu biểu thức $f (x) = \frac{x^{2} + 4 x - 21}{x^{2} - 1}$ ta có:

A. f(x) > 0 khi -7 < x < -1 hoặc 1 < x < 3

B. f(x) > 0 khi x < -7 hoặc -1 < x < 1 hoặc x > 3

C. f(x) > 0 khi -1 < x < 0 hoặc x > 1

D. f(x) > 0 khi x > -1

Xem đáp án

Đáp án: B

Ta có bảng xét dấu:

Dựa vào bảng xét dấu ta thấy: f(x) > 0 khi x < -7 hoặc -1 < x < 1 hoặc x > 3

Bắt đầu thi ngay