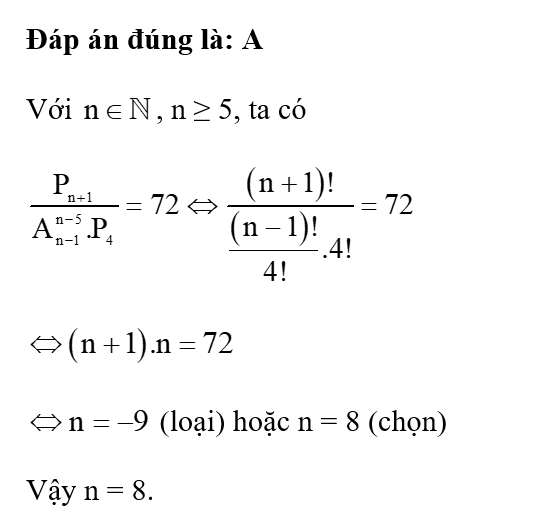10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 KNTT Bài 109. Chỉnh hợp có đáp án

Trắc nghiệm Toán 10 KNTT Bài 109. Chỉnh hợp có đáp án

Đề số 1

Trắc nghiệm Toán 10 KNTT Bài 109. Chỉnh hợp có đáp án

95 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giá trị của $A_{6}^{3}$ là

A. 720;

B. 480;

C. 360;

D. 120.

Xem đáp án

Đáp án đúng là: D

$A_{6}^{3} = \frac{6!}{(6 - 3)!} = \frac{5!}{3!} = 120$ .

Câu 2:

Giá trị của n trong phương trình $2 A_{n}^{2} + A_{n + 2}^{2} = 54$ là

A. 2;

B. 3;

C. 4;

D. 5.

Xem đáp án

Đáp án đúng là: C

Với $n \in ℕ$ , n ≥ 2, ta có

$2 A_{n}^{2} + A_{n + 2}^{2} = 54 \Leftrightarrow 2 n (n - 1) + (n + 2) (n + 1) = 54$

$\Leftrightarrow 3 n^{2} + n - 52 = 0$

$\Leftrightarrow n = - \frac{13}{3}$ (loại) hoặc n = 4 (chọn).

Vậy n = 4.

Câu 3:

Giá trị n thỏa mãn phương trình $\frac{P_{n + 1}}{A_{n - 1}^{n - 5} . P_{4}} = 72$ là

A. 8;

B. 9;

C. 10;

D. 11.

Xem đáp án

Giá trị n thỏa mãn phương trình Pn+1 / A n-5 n -1 . P4= 72 là (ảnh 1)

Câu 4:

Giá trị n thỏa mãn $A_{n}^{8} + A_{n}^{7} = 16 A_{n}^{6}$ là

A. 2;

B. 6;

C. 10;

D. 14.

Xem đáp án

Giá trị n thỏa mãn 8A n+ 7A n= 16 6A n là (ảnh 1)

Câu 5:

Mội giải bóng đá có 20 đội tham dự. Các đội thi đấu với nhau theo thể thức vòng tròn lượt đi và lượt về. Hỏi có bao nhiêu trận đấu diễn ra?

A. 190;

B. 230;

C. 350;

D. 380.

Xem đáp án

Đáp án đúng là: D

Số trận đấu diễn ra là: $A_{20}^{2} = 380$ (trận).

Câu 6:

Trong trận chung kết World Cup 2022, hai đội bóng Argentina và Pháp bước vào loạt đá luân lưu sau 120 phút thi đấu. Mỗi đội cần chọn 5 cầu thủ trong số 11 cầu thủ để lần lượt thực hiện cú sút. Hỏi mỗi đội có bao nhiêu cách chọn để thực hiện loại sút luân lưu?

A. 55 440;

B. 44 330;

C. 33 220;

D. 22 110.

Xem đáp án

Đáp án đúng là: A

Số cách chọn của mỗi đội là $A_{11}^{5} = 55 440$ (cách).

Câu 7:

Tổ 1 gồm 7 bạn nam và 5 bạn nữ xếp thành 1 hàng ngang sao cho đầu hàng và cuối hàng là 2 bạn nữ. Tổ 1 có bao nhiêu cách xếp hàng?

A. 604 800;

B. 479 001 600;

C. 7 257 600;

D. 72 576 000.

Xem đáp án

Đáp án đúng là: D

Số cách chọn 2 bạn nữ đứng đầu hàng là $A_{5}^{2} = 20$ (cách).

Số bạn còn lại là:

7 + 5 – 2 = 10 (bạn).

Số cách xếp 10 bạn còn lại là:

10! = 3 628 800 (cách).

Vậy số cách xếp hàng của tổ 1 là:

20 . 3 628 800 = 72 576 000 (cách).

Câu 8:

Có 4 bạn nam và 3 bạn nữ xếp thành 1 hàng. Có bao nhiêu cách xếp để 2 đầu hàng cùng là bạn nam hoặc bạn nữ?

A. 5040;

B. 2160;

C. 1440;

D. 720.

Xem đáp án

Đáp án đúng là: B

- Trường hợp 1: 2 bạn đầu hàng đều là nam

Số cách chọn 2 bạn nam đầu hàng là $A_{4}^{2} = 12$ (cách).

Số cách xếp các bạn còn lại là 5! = 120 (cách)

Số cách xếp của trường hợp 1 là 12 . 120 = 1440 (cách).

- Trường hợp 2: 2 bạn đầu hàng đều là nữ

Số cách chọn 2 bạn nữ đầu hàng là $A_{3}^{2} = 6$ (cách).

Số cách xếp các bạn còn lại là 5! = 120 (cách)

Số cách xếp của trường hợp 1 là 6 . 120 = 720 (cách).

Vậy tổng số cách xếp thỏa mãn đề bài là 1440 + 720 = 2160 (cách).

Câu 9:

Từ 6 chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số có 3 chữ số khác nhau?

A. 216;

B. 125;

C. 120;

D. 100.

Xem đáp án

Đáp án đúng là: D

Số cách chọn chữ số hàng trăm là 5 cách (trừ chữ số 0).

Số cách chọn 2 chữ số còn lại là $A_{5}^{2} = 20$ (cách).

Vậy số các số có 3 chữ số khác nhau có thể lập được là 5 . 20 = 100 (số).

Câu 10:

Có bao nhiêu số tự nhiên có 4 chữ số khác nhau chia hết cho 5?

A. 1440;

B. 1008;

C. 952;

D. 938.

Xem đáp án

Đáp án đúng là: C

Chữ số hàng đơn vị là 0 hoặc 5.

- Trường hợp 1: Chữ số hàng đơn vị là 0:

Số cách chọn chữ số hàng nghìn là 9 cách (trừ chữ số 0).

Số cách chọn chữ số hàng trăm và hàng chục là $A_{8}^{2} = 56$ (cách).

Số các số trong trường hợp 1 là 1 . 9 . 56 = 504 (cách).

- Trường hợp 2: Chữ số hàng đơn vị là 5:

Số cách chọn chữ số hàng nghìn là 8 cách (trừ chữ số 0 và 5).

Số cách chọn chữ số hàng trăm và hàng chục là $A_{8}^{2} = 56$ (cách).

Số các số trong trường hợp 2 là 1 . 8 . 56 = 448 (cách).

Vậy số các số tự nhiên có 4 chữ số khác nhau và chia hết cho 5 là 504 + 448 = 952 (số).

Bắt đầu thi ngay