14 câu hỏi trắc nghiệm thuộc Ôn tập chương II

Câu 1:

Tập xác định của hàm số $y = \sqrt{3 x + 2} + \frac{1}{3 |x| - 2}$ là:

A. $[- \frac{2}{3}; + \infty)$

B. $(- \frac{2}{3}; + \infty)$

C. $(- \frac{2}{3}; + \infty) \ \{\frac{2}{3}\}$

D. $ℝ \ \{\pm \frac{2}{3}\}$

Hàm số được xác định khi $\{\begin{cases} 3 x + 2 \geq 0 \\ 3 |x| - 2 \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \geq - \frac{2}{3} \\ x \neq \pm \frac{2}{3} \end{cases} \Leftrightarrow \{\begin{cases} x > - \frac{2}{3} \\ x \neq \frac{2}{3} \end{cases}$ .

Vậy tập xác định của hàm số là: $(\frac{- 2}{3}; + \infty) \ \{\frac{2}{3}\}$

Câu 2:

Hàm số $y = |x + 2| - |x - 2|$ là hàm số:

A. chẵn trên $ℝ$

B. lẻ trên $ℝ$

C. không chẵn và không lẻ

D. nghịch biến trên $ℝ$

Xem đáp án

Đặt $f (x) = |x + 2| - |x - 2|$ thì tập xác định của f(x) là $ℝ$ . Ta có:

$f (- x) = |- x + 2| - |- x - 2| = |x - 2| - |x + 2| = - f (x)$ .

Vậy f(x) là một hàm số lẻ.

Câu 3:

Khẳng định nào sau đây đúng nhất?

A. Hàm số $y = |x - 3|$ đồng biến trên $(3; + \infty)$

B. Hàm số C nghịch biến trên $(- \infty; 3)$

C. Hàm số $y = |x - 3|$ đồng biến trên $(- \infty; 3)$

D. Cả hai khẳng định A và B đều đúng

Xem đáp án

Ta có $y = |x - 3| = \{\begin{cases} x - 3 k h i x \geq 3 \\ - x + 3 k h i x < 3 \end{cases}$ .

Trên khoảng $(3; + \infty)$ thì y = x – 3 có hệ số a= 1 >0 nên hàm số đồng biến trên khoảng này.

Trên khoảng $(- \infty; 3)$ thì y = - x + 3 có hệ số a= -1 < 0 nên hàm số nghịch biến trên khoảng này.

Câu 4:

Đường thẳng nào trong các đường thẳng sau đây song song với đường thẳng y = -2x?

A. $y + 2 x - 1 = 0$

B. $y = 2 x - 1$

C. $y - 4 x + 1 = 0$

D. $y = 2 x$

Xem đáp án

Hai đường thẳng song song với nhau nếu chúng có cùng hệ số góc và tung độ gốc khác nhau.

Ta có: y + 2x – 1 = 0 $\Leftrightarrow$ y = -2x + 1

Suy ra; đường thẳng y = - 2x + 1 song song với đường thẳng y = -2 x.

Chọn A.

Câu 5:

Đường thẳng đi qua điểm M (2;-1) và vuông góc với đường thẳng $y = \frac{1}{2} x - 3$ có phương trình là:

A. $2 x + y - 3 = 0$

B. $2 x + y - 1 = 0$

C. $2 x - y - 3 = 0$

D. $y = - 2 x + 2$

Xem đáp án

Gọi phương trình đường thẳng (d) cần tìm là: y = ax + b.

Vì đường thẳng này vuông góc với đường thẳng $y = \frac{1}{2} x - 3$ nên:

$a . \frac{1}{2} = - 1 \Leftrightarrow a = - 2$ ( hai đường thẳng vuông góc với nhau có tích hai hệ số góc bằng -1).

Vậy đường thẳng d: y = - 2x + b

Đường thẳng này đi qua M(2; -1) nên -1 = - 2.2+ b nên b = 3.

Vậy phương trình đường thẳng d: y = -2x + 3 hay 2x + y – 3 = 0

Câu 6:

Đường thẳng (d) với hệ số góc dương, cắt trục hoành tại P(-3;0) và cắt trục tung tại Q sao cho diện tích tam giác OPQ bằng 3 (đvdt) có phương trình là:

A. $y = - \frac{2}{3} x - 2$

B. $y = \frac{2}{3} x + 2$

C. $y = \frac{3}{2} x + \frac{9}{2}$

D. $y = - \frac{3}{2} x - \frac{9}{2}$

Xem đáp án

Do hệ số góc dương nên ta loại phương án A và D, chỉ còn lại phương án B và C.

Gọi (d) cắt trục tung tại Q(0; b) với b > 0 .

Ta có OP = 3; OQ = b nên diện tích tam giác OPQ là:

$S_{∆ O P Q} = \frac{O P . O Q}{2} = \frac{3 . b}{2} = 3 \Rightarrow b = 2$ .

Vậy đường thẳng d cần tìm là: $y = \frac{2}{3} x + 2$

Chú ý: cả hai đường thẳng $y = \frac{2}{3} x + 2$ và $y = \frac{3}{2} x + \frac{9}{2}$ đều cắt trục hoành tại P(-3;0) nên dấu hiệu này không phân biệt được hai đáp án B và C.

Câu 7:

Hàm số $y = x^{2} - 6 x + 3$ đồng biến trên:

A. $ℝ$

B. $(- \infty; 3)$

C. $(3; + \infty)$

D. $(- \infty; 5)$

Xem đáp án

Ta có: $\frac{- b}{2 a} = \frac{6}{2.1} = 3$

Suy ra, hàm số y = x² – 6x + 3 đồng biến trên khoảng $(3; + \infty)$ .

Câu 8:

Parabol có đỉnh I(0,-1) và đi qua điểm M(2;3) có phương trình là:

A. $y = x^{2} - 4 x - 1$

B. $y = {(x - 1)}^{2} + 2$

C. $y = {(x + 1)}^{2} - 1$

D. $y = x^{2} - 1$

Xem đáp án

Gọi phương trình của parabol cần tìm là : y = ax² + bx + c.

Vì Parabol có đỉnh I(0 ; -1) và đi qua điểm M(2 ; 3) nên :

$\{\begin{cases} - 1 = a . 0^{2} + b . 0 + c \\ \frac{- b}{2 a} = 0 \\ 3 = a . 2^{2} + b . 2 + c \end{cases} \Leftrightarrow \{\begin{array}{l} c = - 1 \\ b = 0 \\ 4 a + 2 b + c = 3 \end{array} \Leftrightarrow \{\begin{cases} c = - 1 \\ b = 0 \\ a = 1 \end{cases}$

Vậy phương trình của parabol cần tìm là: y = x² – 1

Câu 9:

Tọa độ giao điểm của parabol $y = x^{2} - 2 x - 1$ và đường thẳng $y = 2 x + 4$ là:

A. $(- 1; 2) v à (5; 14)$

B. $(2; 1) v à (5; 14)$

C. $(1; 2) v à (5; 14)$

D. $(- 1; 2) v à (- 5; 14)$

Xem đáp án

Phương trình hoành độ giao điểm: x² – 2x – 1 = 2x + 4

$\Leftrightarrow x^{2} - 2 x - 1 - 2 x - 4 = 0 \Leftrightarrow x^{2} - 4 x - 5 = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \Rightarrow y = 2 \\ x = 5 \Leftrightarrow y = 14 \end{array}$

Vậy tọa độ giao điểm của hai đồ thị là (-1; 2) và ( 5; 14).

Câu 10:

Tìm m để đồ thị hàm số $y = x^{2} - 9 |x|$ cắt đường thẳng y = m tại bốn điểm phân biệt.

A. m > 0

B. m > $- \frac{81}{4}$

C. $- \frac{81}{4}$ < m < 0

D. m < -3

Xem đáp án

Đồ thị hàm số $y = x^{2} - 9 |x|$ cắt đường thẳng $y = m$ tại bốn điểm phân biệt khi và chỉ khi phương trình $x^{2} - 9 |x| = m$ (1) có bốn nghiệm phân biệt.

Đặt $t = |x| \Rightarrow t^{2} = x^{2}$ phương trình (1) trở thành: t² – 9t = m hay t² – 9t - m= 0 (2)

Để phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (2) có 2 nghiệm dương phân biệt:

$\Leftrightarrow \{\begin{cases} ∆ = 81 + 4 m > 0 \\ \frac{c}{a} = - m > 0 \\ - \frac{b}{a} = 9 > 0 \end{cases} \Leftrightarrow \{\begin{cases} m > - \frac{81}{4} \\ m < 0 \end{cases} \Leftrightarrow - \frac{81}{4} < m < 0$ .

Câu 11:

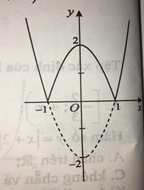
Hình vẽ bên là đồ thị của hàm số:

A. $y = 2 x^{2} - 2$

B. $y = - 2 x^{2} + 2$

C. $y = |2 x^{2} - 2|$

D. $y = |2 x^{2} + 2|$

Xem đáp án

Đồ thị hàm số không phải là parabol nên loại phương án A và B.

Đồ thị đi qua hai điểm có tọa độ là (-1;0) và (1;0). Nhận thấy với $x = \pm 1$ và y = 0 chỉ thỏa mãn $y = |2 x^{2} - 2|$ mà không thỏa mãn $y = |2 x^{2} + 2|$ .

Suy ra; hình vẽ đã cho là của đồ thị hàm số $y = |2 x^{2} - 2|$ .

Chọn C.

Câu 12:

Cho các hình vẽ sau:

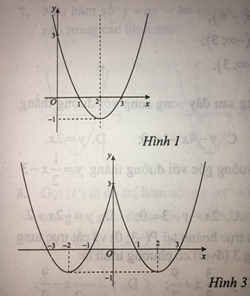
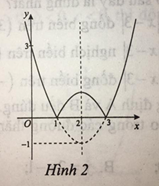
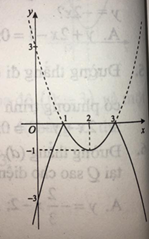
a) Hình vẽ nào là đồ thị của hàm số $y = x^{2} - 4 x + 3$ ?

A. Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

Xem đáp án

Đồ thị của hàm số y = x² – 4x + 3 là đường cong parabol nên chọn A.

Câu 13:

Cho các hình vẽ sau:

b) Hình vẽ nào là đồ thị hàm số $y = x^{2} - 4 |x| + 3$ ?

A. Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

Xem đáp án

Hàm số $y = x^{2} - 4 |x| + 3$ là hàm số chẵn nhận trục Oy làm trục đối xứng nên chỉ có hình 3 thỏa mãn .

Câu 14:

Cho các hình vẽ sau:

c) Hình vẽ nào là đồ thị của hàm số $y = |x^{2} - 4 x + 3|$ ?

A. Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

Xem đáp án

Ta có: $y = |x^{2} - 4 x + 3| = \{\begin{cases} x^{2} - 4 x + 3 k h i x^{2} - 4 x + 3 \geq 0 \\ - (x^{2} - 4 x + 3) k h i x^{2} - 4 x + 3 < 0 \end{cases}$

Cách vẽ đồ thị $y = |x^{2} - 4 x + 3|$

+ Vẽ đồ thị hàm số y = x² – 4x + 3 (C).

+ Giữ nguyên phần đồ thị (C) phía trên trục hoành

Lấy đối xứng phần dưới trục hoành qua trục hoành; xóa phần đồ thị (C) dưới trục hoành.

Khi đó, ta được đồ thị hàm số $y = |x^{2} - 4 x + 3|$ .

Chọn B