10 câu hỏi trắc nghiệm thuộc Dạng 4. Lập phương trình chính tắc của parabol

Câu 1:

Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình đường chuẩn $x + \frac{1}{2} = 0$ . Phương trình chính tắc của parabol (P) là

A.y² = 4x;

B. y² = x ;

C. $y^{2} = \frac{1}{2} x$ ;

D. y² = 2x.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Parabol (P) có phương trình đường chuẩn $x + \frac{1}{2} = 0$ hay $x = - \frac{1}{2} .$

Do đó $\frac{p}{2} = \frac{1}{2}$ nên p = 1.

Vậy phương trình chính tắc của parabol (P) là y² = 2x.

Câu 2:

Trong mặt phẳng tọa độ Oxy, cho parabol (P): y² = 2px (p > 0) có tiêu điểm F(5; 0). Phương trình chính tắc của (P) là

A.y² = 5x;

B. $y^{2} = \frac{5}{2} x$ ;

C. y² = 20x;

D. y = 20x².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Do tọa độ tiêu điểm của (P) là F(5; 0) nên ta có $\frac{p}{2} = 5,$ suy ra p = 10 nên 2p = 20.

Vậy phương trình chính tắc của parabol (P) là : y² = 20x.

Câu 3:

Trong mặt phẳng tọa độ Oxy, cho parabol (P): y² = 2px (p > 0). Biết rằng khoảng cách từ tiêu điểm F đến đường thẳng Δ: x + y – 12 = 0 bằng $2 \sqrt{2} .$ Phương trình chính tắc của (P) là

A. y² = 16x hoặc y² = 32x;

B. y² = –16x hoặc y² = 32x;

C. y² = 32x hoặc y² = 64x;

D. y² = –32x hoặc y² = 64x.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Gọi tọa độ tiêu điểm của (P) là $F (\frac{p}{2}; 0) .$

Khoảng cách từ F đến Δ là $2 \sqrt{2}$ nên ta có: $d (F, Δ) = \frac{|\frac{p}{2} - 12|}{\sqrt{1^{2} + 1^{2}}} = 2 \sqrt{2}$

$\Leftrightarrow |\frac{p}{2} - 12| = 4 \Leftrightarrow [\begin{matrix} p = 16 \\ p = 32 \end{matrix}$ .

Vậy phương trình chính tắc của (P) là: y² = 32x hoặc y² = 64x.

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho parabol (P): y² = 2px (p > 0) có khoảng cách từ đỉnh tới tiêu điểm bằng $\frac{3}{4} .$ Phương trình chính tắc của (P) là

A. y² = 3x;

B. y² = 6x;

C. $y^{2} = \frac{3}{4} x;$

D.

y^{2} = \frac{3}{2} x;

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Khoảng cách từ đỉnh O đến tiêu điểm $F (\frac{p}{2}; 0)$ là $\frac{p}{2}$

Theo bài, ta có $\frac{p}{2} = \frac{3}{4},$ suy ra $p = \frac{3}{2}$ nên 2p = 3.

Vậy phương trình chính tắc của (P) là y² = 3x.

Câu 5:

Trong mặt phẳng tọa độ Oxy, cho parabol (P): y² = 2px (p > 0). Parabol (P) cắt đường thẳng Δ: 3x – y = 0 tại hai điểm phân biệt A, B sao cho Phương trình chính tắc của (P) là

A. y² = –18x;

B. y² = 81x;

C. y² = 9x;

D. y² = 18x.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Đường thẳng Δ: 3x – y = 0 hay y = 3x.

Phương trình hoành độ của (P) và Δ là: (3x)² = 2px ⇔ x(9x – 2p) = 0

⇔ x = 0 hoặc $x = \frac{2 p}{9} .$

Tọa độ hai giao điểm của (P) và Δ là $A (0; 0), B (\frac{2 p}{9}; \frac{2 p}{3}) .$

Khi đó ta có $A B = \sqrt{{(\frac{2 p}{9})}^{2} + {(\frac{2 p}{3})}^{2}} = \frac{2 p \sqrt{10}}{9} .$

Mà theo bài, $A B = 2 \sqrt{10} .$ Do đó $\frac{2 p \sqrt{10}}{9} = 2 \sqrt{10} \Leftrightarrow p = 9.$

Vậy phương trình chính tắc của (P) là y² = 18x.

Câu 6:

Trong mặt phẳng tọa độ Oxy, cho parabol (P) biết một dây cung của (P) vuông góc với trục Ox có độ dài bằng 8 và khoảng cách từ đỉnh O của (P) đến dây cung này bằng 1. Phương trình chính tắc của (P) là

A. y² = 16x;

B. y² = 32x;

C. y² = 24x;

D. y² = 12x.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

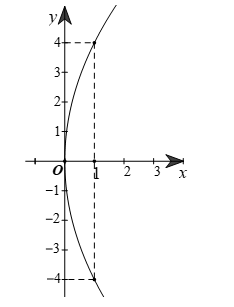
Trong mặt phẳng tọa độ Oxy, cho parabol (P) biết một dây cung của (P) vuông góc với trục Ox có độ (ảnh 1)

Gọi phương trình chính tắc của parabol (P) là: y² = 2px (p > 0).

Vì một dây cung của (P) vuông góc với trục Ox có độ dài bằng 8 và khoảng cách từ đỉnh O của (P) đến dây cung này bằng 1 nên điểm A(1; 4) thuộc vào (P) suy ra 16 = 2.p.1 nên p = 8.

Vậy (P): y² = 16x.

Câu 7:

Trong mặt phẳng tọa độ Oxy, cho parabol (P) cắt elip (E): 4x² + 6y² = 24 tại 2 điểm A, B sao cho AB = 2. Phương trình chính tắc của parabol (P) là

A. $y^{2} = \frac{\sqrt{2}}{6} x$ ;

B. $y^{2} = \frac{\sqrt{2}}{3} x$ ;

C. $y^{2} = \frac{\sqrt{2}}{12} x$ ;

D.

y^{2} = \frac{\sqrt{2}}{2} x

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Gọi phương trình chính tắc của parabol (P) là: y² = 2px (p > 0).

Ta có (E): 4x² + 6y² = 24 $\Leftrightarrow \frac{x^{2}}{6} + \frac{y^{2}}{4} = 1.$

Do (E) và (P) có đồ thị đối xứng qua trục Ox và AB = 2 suy ra A(t; 1), B(t; –1) là hai giao điểm nằm bên phải Oy nên t > 0.

Vì A(t; 1) ∈ (E) nên ta có 4t² + 6.1² = 24 $\Leftrightarrow t^{2} = \frac{9}{2} \Leftrightarrow t = \frac{3}{\sqrt{2}} .$

Do đó $A (\frac{3}{\sqrt{2}}; 1) \in (P)$ nên ta có $1^{2} = 2 p \cdot \frac{3}{\sqrt{2}},$ do đó $p = \frac{\sqrt{2}}{6} .$

Vậy $(P) : y^{2} = \frac{\sqrt{2}}{3} x .$

Câu 8:

Đường thẳng d: y = kx (k ≠ 0) đi qua gốc O, cắt (P): y² = 16x tại A (A khác O). Tập hợp trung điểm của đoạn OA là đồ thị có phương trình là

A. y² = 2x;

B. y² = 8x;

C. $y^{2} = \frac{1}{2} x$ ;

D. y² = 4x.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Phương trình tung độ giao điểm của d và (P) là: $y^{2} = \frac{16 y}{k} \Rightarrow [\begin{array}{l} y = 0 \\ y = \frac{16}{k} \end{array}$ .

Suy ra tọa độ điểm $A (\frac{16}{k^{2}}; \frac{16}{k})$ . Tọa độ trung điểm M của OA là $M (\frac{8}{k^{2}}; \frac{8}{k})$ .

Do đó ta có $x_{M} = \frac{8}{k^{2}}$ và $y_{M} = \frac{8}{k}$

Suy ra $y_{M}^{2} = \frac{64}{k^{2}}$ nên $y_{M}^{2} = 8 x_{M}$

Vậy tập hợp điểm M là parabol (P) có phương trình y² = 8x.

Câu 9:

Phương trình chính tắc của parabol đi qua điểm A(4; 9) là

A. y² = 2x;

B. y² = 8x;

C. $y^{2} = \frac{81}{4} x$ ;

D. y² = 4x.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Gọi phương trình chính tắc của parabol cần tìm có dạng y² = 2px (p > 0).

Parabol đi qua điểm A(4; 9) nên ta có: 9² = 2p.4 suy ra $p = \frac{81}{8}$

Vậy phương trình chính tắc của parabol cần tìm là $y^{2} = \frac{81}{4} x$ .

Câu 10:

Trong mặt phẳng tọa độ Oxy, cho parabol (P) đi qua điểm M có hoành độ bằng 2 và khoảng cách từ M đến tiêu điểm bằng $\frac{5}{2} .$ Phương trình chính tắc của parabol (P) là

A. y² = 8x;

B. y² = 4x;

C. y² = 2x;

D. y² = x.

Xem đáp án