Trắc nghiệm Toán 10 CTST Bài 3: Đường tròn trong mặt phẳng tọa độ (Phần 2) có đáp án
Trắc nghiệm Toán 10 CTST Bài 3: Đường tròn trong mặt phẳng tọa độ (Vận dụng) có đáp án
-
1428 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1: và d2: . Gọi (C) là đường tròn tiếp xúc với d1 tại điểm A có hoành độ dương, (C) cắt d2 tại hai điểm B, C sao cho tam giác ABC vuông tại B và có diện tích bằng . Phương trình của đường tròn (C) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
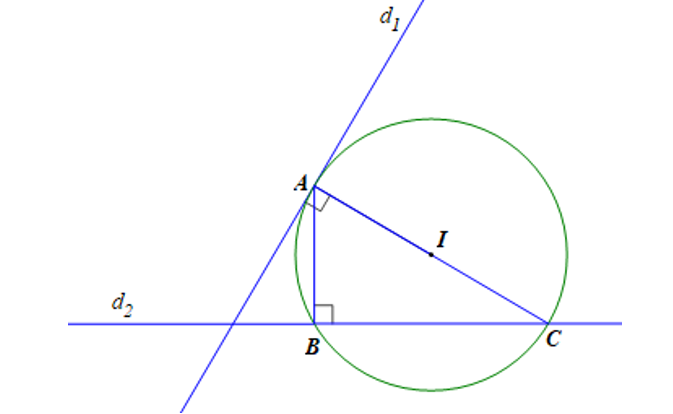
Vì A ∈ d1 nên
B, C ∈ d2 nên .
Suy ra
Đường thẳng d1: có vectơ pháp tuyến là nên có vectơ chỉ phương là .
Đường thẳng d2: có vectơ pháp tuyến là nên có vectơ chỉ phương là .
Ba điểm A, B, C đều nằm trên đường tròn mà tam giác ABC vuông tại B
Do đó AC là đường kính của đường tròn (C).
AC ⊥ d1
c – a – 3c – 3a = 0 Û 2a + c = 0 (1).
Lại có tam giác ABC vuông tại B nên AB ⊥ d2
b – a + 3b + 3a = 0 a + 2b = 0 (2).
Mặt khác
(do a > 0)
2a|c – b| = 1 (3)
Từ (1) và (2) suy ra 2(2a + c) – (a + 2b) = 2 Û 2c – 2b = –3a
Thay vào (2) ta được a.|–3a| = 1 Û 3a2 = 1 (do a > 0)
(do a > 0).
Khi đó
và
Đường tròn (C) có AC là đường kính nên nhận trung điểm của AC làm tâm và bán kính .
Vậy phương trình đường tròn cần tìm là
Câu 2:
Phương trình tiếp tuyến đi qua điểm A(5; –2) của đường tròn (C): (x – 1)2 + (y + 2)2 = 8 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Đường tròn (C) có tâm I(1; –2) và bán kính R = .
Giả sử tiếp tuyến có vectơ pháp tuyến là (a2 + b2 ≠ 0).
Phương trình tiếp tuyến d đi qua điểm A(5; –2) và nhận làm vectơ pháp tuyến là:
a(x – 5) + b(y + 2) = 0 hay ax + by – 5a + 2b = 0.
Ta có:
|a – 2b – 5a + 2b| =
(– 4a)2 = 8(a2 + b2)
16a2 – 8a2 = 8b2
a2 = b2
a = b hoặc a = – b.
Với a = b, chọn b = 1 thì a = 1.
Khi đó phương trình d là x + y – 3 = 0.
Với a = – b, chọn b = – 1 thì a = 1.
Khi đó phương trình d là x – y – 7 = 0.
Vậy ta chọn phương án B.
Câu 3:
Cho phương trình x2 + y2 – 2(m + 1)x + 4y – 1 = 0 (1). Với giá trị nào của m thì (1) là phương trình đường tròn có bán kính nhỏ nhất?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có x2 + y2 – 2(m + 1)x + 4y – 1 = 0 có a = m + 1; b = –2 và c = –1.
Để (1) là phương trình đường tròn thì a2 + b2 – c > 0
(m + 1)2 + (–2)2 – (–1) > 0
(m + 1)2 + 5 > 0 (luôn đúng với mọi m).
Khi đó bán kính của đường tròn này là
Hay R2 = (m + 1)2 + 5 ≥ 5, với mọi m.
Dấu “=” xảy ra khi và chỉ khi m + 1 = 0 m = –1.
Vậy đường tròn có bán kính nhỏ nhất bằng khi m = –1.
Câu 4:
Cho tiếp tuyến d của một đường tròn có phương trình: x – y = 0. Biết bán kính của đường tròn này bằng 2 và điểm O(0;0) thuộc đường tròn. Hỏi có bao nhiêu phương trình đường tròn tâm I có tiếp tuyến trên?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Gọi M là tiếp điểm của tiếp tuyến với đường tròn.
Khi đó IM vuông góc với tiếp tuyến.
Phương trình tiếp tuyến của đường tròn là: x – y = 0 có vectơ pháp tuyến .
Đường thẳng IM có vectơ pháp tuyến nên phương trình có dạng: x + y + c = 0.
Điểm I nằm trên đường thẳng IM nên ta có I(t; – c – t)
O nằm trên đường tròn nên OI = R = 2
Do đó t2 + (– c – t)2 = 4.
Mặt khác, IM vuông góc với tiếp tuyến nên khoảng cách từ I đến tiếp tuyến d bằng 2.
Hay
Khi thì ta có:
Với 2 giá trị của t, suy ra có 2 điểm I.
Khi thì ta có:
Với 2 giá trị của t, suy ra có 2 điểm I.
Vậy có 4 phương trình đường tròn thỏa mãn.
Câu 5:
Cho đường tròn (C): (x + 1)2 + (y – 1)2 = 25 và điểm M(9; – 4). Gọi d là tiếp tuyến của (C), biết d đi qua M và không song song với các trục toạ độ. Khi đó khoảng cách từ điểm P(6; 5) đến d bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Đường tròn (C) có tâm I(–1; 1) và R = 5.
Ta có
Giả sử tiếp tuyến d có vectơ pháp tuyến là (với a, b ≠ 0 do d không song song với các trục toạ độ).
Khi đó tiếp tuyến d đi qua điểm M(9; – 4) nên có phương trình:
a(x – 9) + b(y + 4) = 0 ax + by – 9a + 4b = 0.
Đường thẳng d là tiếp tuyến của đường tròn nên d(I, d) = R
52 . (b – 2a)2 = 52 . (a2 + b2) b2 – 4ab + 4a2 = a2 + b2
3a2 – 4ab = 0 Û a(3a – 4b) = 0
3a = 4b.
Chọn b = 3 thì a = 4.
Khi đó d có phương trình là:
4x + 3y – 36 + 12 = 0 hay 4x + 3y – 24 = 0.
Do đó d(P; d) =
