25 câu hỏi trắc nghiệm thuộc 160 câu trắc nghiệm Phương pháp tọa độ trong mặt phẳng (P4)

Câu 1:

Phương trình nào sau đây là phương trình của đường tròn?

(I) x²+ y² – 4x +15y -12= 0.

(II) x²+ y² – 3x +4y +20= 0.

(III) 2x²+ 2y²- 4x + 6y +1= 0 .

A. Chỉ (I).

B. Chỉ (II).

C. Chỉ (III).

D. Chỉ (I) và (III).

Xem đáp án

Ta xét các phương án:

(I) có:

(II) có:

(III) tương đương : x²+ y² – 2x - 3y + 0,5= 0.

phương trình này có:

Vậy chỉ (I) và (III) là phương trình đường tròn.

Chọn D.

Câu 2:

Mệnh đề nào sau đây đúng?

(1) Đường tròn (C₁) : x²+ y² – 2x +4y - 4= 0 có tâm I( 1; -2) bán kính R= 3.

(2) Đường tròn (C₂) x²+ y² – 5x +3y – 0,5= 0 có tâm bán $I (\frac{5}{2}; - \frac{3}{2})$ kính R= 3.

A. Chỉ (1).

B. Chỉ (2).

C.cả hai

D. Không có.

Xem đáp án

Ta có: đường tròn (C₁) :

Vậy (1) đúng

Đường tròn ( C₂):

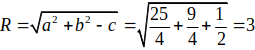
Vậy (2) đúng.

Chọn C.

Câu 3:

Cho đường tròn (C) : x²+ y²- 4x + 3= 0 . Hỏi mệnh đề nào sau đây sai?

A. tâm I( 2; 0)

B. bán kính R= 1

C. (C) cắt trục 0x tại 2 điểm.

D. (C) cắt trục Oy tại 2 điểm.

Xem đáp án

Cho x= 0 ta được: y²+ 3= 0 phương trình vô nghiệm.

Vậy (C) không có điểm chung nào với trục tung.

Chọn D.

Câu 4:

Cho đường tròn (C) : x²+ y²+ 8x+ 6y+ 9= 0. Mệnh đề nào sau đây sai?

A. (C) không đi qua điểm O.

B. tâm I( -4; -3).

C.bán kính R= 4.

D. (C) đi qua điểm M(-1; 0) .

Xem đáp án

+Ta có a= -4; b= -3 ; c= 9 và a²+ b²- c= 16+ 9 - 9 = 16> 0

Suy ra (C) là đường tròn tâm I( -4; -3) và R= 4

Vậy B; C đúng.

+Thay O vào (C) ta có: 0²+ 0²+ 8.0+ 6.0 + 9= 0 vô lí . Vậy A đúng.

+Thay M( -1; 0) vào (C) ta có: (-1) ²+ 0²+ 8.(-1) + 6.0 + 9= 0 ( vô lý). Vậy D sai.

Chọn D.

Câu 5:

Đường tròn x²+ y²- 10x -11= 0 có bán kính bằng bao nhiêu?

A.6

B.2

C. 4

D. $\sqrt{6}$

Xem đáp án

Ta có hệ số a= 5; b= 0 và c= -11 nên bán kính là R= $\sqrt{a^{2} + b^{2} - c} = 6$

Chọn A.

Câu 6:

Cho hai điểm A( 5; -1) ; B( -3; 7) . Đường tròn có đường kính AB có phương trình là

A.x²+ y²+ 2x- 6y - 22= 0.

B. .x²+ y²- 2x- 6y - 22= 0.

C. .x²+ y²- 2x- y + 1= 0.

D. Tất cả sai

Xem đáp án

Tâm I của đường tròn là trung điểm AB nên I( 1; 3) .

Bán kính

Vậy phương trình đường tròn là: (x-1)²+ (y-3) ²= 32

Hay x²+ y²- 2x- 6y - 22= 0.

Chọn B.

Câu 7:

Cho hai điểm A( -4; 2) và B(2; -3). Tập hợp điểm M thỏa mãn $M A^{2} + M B^{2} = 31$ có phương trình là

A. x²+ y² + 2x + 6 y + 1= 0.

B. x²+ y²- 6x- y + 1= 0.

C. x²+ y²- 2x- 6y – 10 = 0.

D. x²+ y² + 2x + y + 1 = 0.

Xem đáp án

Ta có: $\vec{M A} (x + 4; y - 2); \vec{M B} (x - 2; y + 3)$

Theo giả thiết: MA²+ MB²= 31

Tương đương : ( x+ 4) ²+ (y-2) ²+ (x-2) ²+ (y+3) ²= 31

Hay x²+ y²+ 2x + y+= 0

Chọn D.

Câu 8:

Đường tròn (C) tâm I( -4; 3) và tiếp xúc với trục tung có phương trình là

A. x²+ y² - 4x + 3y + 1 = 0.

B. (x+ 4) ²+ (y- 3) ²= 16.

C.(x-4) ²+ (y+ 3) ²= 9.

D. x²+ y² + 8x -6 y + 1 = 0.

Xem đáp án

Do đường tròn (C) tiếp xúc với trục tung Oy và có tâm I( -4; 3) nên:

a= - 4; b= 3 và R= |a| =4.

Do đó, (C) có phương trình: (x+ 4) ²+ (y- 3) ²= 16.

Chọn B.

Câu 9:

Đường tròn (C) tâm I( 4;3) và tiếp xúc với đườngthẳng ∆: 3x - 4y + 5= 0 có phương trình là

A.(x-4) ²+ (y-3) ²= 2.

B.(x-4) ²+ (y-3) ²= 1.

C. (x-4) ²+ (y-3) ²= 4.

D. (x-4) ²+ (y-3) ²= 3

Xem đáp án

Đường tròn (C) có bán kính

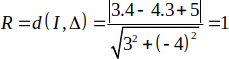
Do đó, (C) có phương trình : (x-4) ²+ (y-3) ²= 1.

Chọn B.

Câu 10:

Đường tròn 2x²+ 2y²-8x +4y- 4 = 0 có tâm là điểm nào trong các điểm sau đây ?

A. (8; -4)

B.( 4; -2)

C.( -4;2)

D.(2; -1 )

Xem đáp án

Ta viết lại phương trình đường tròn: x²+ y²- 4x + 2y- 2= 0

Ta có: $\{\begin{cases} 4 = 2 a \\ - 2 = 2 b \end{cases} \to \{\begin{cases} a = 2 \\ b = - 1 \end{cases}$ nên tâm I( 2; -1) .

Chọn D.

Câu 11:

Đường tròn 3x²+ 3y²-6x +9y – 9= 0 có bán kính bằng bao nhiêu ?

A. 2,5

B.3

C.2

D. 4

Xem đáp án

Ta viết lại phương trình đường tròn: x²+ y²-2x + 3y -3= 0

_{Suy ra a= 1; b= -1,5 và c= -3 và bán kính R= $\sqrt{1^{2} + 1, 5^{2} + 3^{2}} = \frac{5}{2}$}

_{Chọn A.}

Câu 12:

Cho đường cong (C): x²+ y²- 8x +10y +m= 0. Với giá trị nào của m thì (C) là đường tròn có bán kính bằng 7 ?

A.m= 4

B.m= 8

C.m= -8

D.m= -2

Xem đáp án

Ta có hệ số a= 4; b= -5 và c= m.

Để C là đường tròn có bán kính R= 7 thì:

$R = \sqrt{4^{2} + 5^{2} - m} = 7 \Leftrightarrow m = - 8$

Chọn C.

Câu 13:

Đường tròn tâm I( 3; -2) và bán kính R= 2 có phương trình là

A.( x+ 3) ²+ (y+2) ²= 2

B.(x-3)²+ (y+ 2)²= 4

C. ( x+ 3) ²+(y-2) ²=4

D.(x-3)²+ (y-2) ²= 4

Xem đáp án

Phương trình đường tròn có tâm (3; -2) , bán kính R= 2 là:

(x-3)²+ (y+ 2)²= 4

Chọn B.

Câu 14:

Đường tròn tâm I( -1; 2) và đi qua điểm M( 2;1) có phương trình là

A.x²+ y²+ 2x+ 4y - 5= 0.

B x²+ y²+ 2x - 4y - 5= 0.

C. x²+ y²+ 2x+ 4y + 5= 0.

D. x²+ y²- 2x+ 4y - 5= 0.

Xem đáp án

Đường tròn có tâm I( -1; 2) và đi qua M( 2; 1) thì. có bán kính là:

R= IM = $\sqrt{3^{2} + {(- 1)}^{2}}$ = $\sqrt{10}$

Khi đó có phương trình là: (x+ 1) ²+ ( y-2) ²=10

Hay x²+ y²+ 2x - 4y - 5= 0.

Chọn B.

Câu 15:

Cho hai điểm A( 5; -1) và B( -3; 7). Đường tròn có đường kính AB có phương trình là

A. x²+y²-2x+6y-3= 0.

B. x²+y²-2x- 6y- 22 = 0

C. x²+y² + 2x+6y-3= 0

D. x²+y²+ 2x+6y- 15= 0

Xem đáp án

Tâm I của đường tròn là trung điểm của AB nên I( 1;3) .

Bán kính

Vậy phương trình đường tròn là:

(x-1) ²+ (y-3) ²= 32 hay . x²+y²-2x- 6y- 22 = 0

Chọn B.

Câu 16:

Cho đường thẳng $∆ : \{\begin{cases} x = 2 - 3 t \\ y = 1 + 2 t \end{cases}$ . Hoành độ hình chiếu của M( 4; 5) trên $∆$ gần nhất với số nào sau đây ?

A. (1,1)

B. (1,2)

C. (1,4)

D. (1,5)

Xem đáp án

Gọi H là hình chiếu của M trên ∆

Ta có: H thuộc ∆ nên H( 2-3t ; 1+ 2t) MH =(-2-3t; -4+2t)

Đường thẳng $∆$ có vectơ chỉ phương là $\vec{u}$ = ( 3; -2)

Ta có $\vec{M H} ⊥ \vec{u} \Leftrightarrow \vec{M H} . \vec{u} = 0$

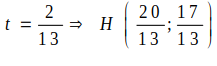
Chọn D

Câu 17:

Cho hai đường thẳng d: x + 2y + 3= 0 và d’: 2x+ y + 3= 0. Phương trình các đường phân giác của các góc tạo bởi d

và d’ là:

A.x+ y= 0 và x – y + 4= 0 .

B. x-y+ 4= 0 và x+ y-2= 0 .

C. x+ y+ 2= 0 và x- y= 0

D. x+ y+ 1= 0 và x-y- 3= 0 .

Xem đáp án

Phương trình các đường phân giác của các góc tạo bởi d và d’ là:

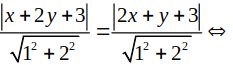
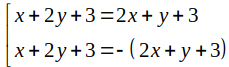
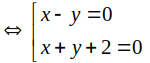
Chọn C.

Câu 18:

Tính góc giữa hai đường thẳng: 3x+ y- 1= 0 và 4x- 2y – 4= 0.

A. 30⁰

B. 45⁰

C. 60⁰

D. 90⁰

Xem đáp án

Đường thẳng: 3x + y- 1= 0 có vtpt $n_{1}$ =(3;1)

Đường thẳng: 4x -2y -4= 0 có vtpt $n_{2}$ =(4;-2)

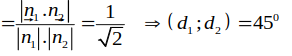
Chọn B.

Câu 19:

Tìm côsin góc giữa 2 đường thẳng d₁: x+ 2y -7= 0 và d₂: 2x- 4y+ 9= 0.

A. $- \frac{3}{5}$

B. $\frac{2}{\sqrt{5}}$

C. $\frac{1}{5}$

D. $\frac{3}{\sqrt{5}}$

Xem đáp án

Vectơ pháp tuyến của đường thẳng d₁ là n1=(1;2)

Vectơ pháp tuyến của đường thẳng d₂ là n2=(2;-4)

Gọi $φ$ là góc giữa 2 đường thẳng ta có:

$\cos φ = \frac{n_{1} . n_{2}}{|n_{1}| . |n_{2}|} = - \frac{3}{5}$

Chọn A.

Câu 20:

Tìm góc giữa 2 đường thẳng d: 6x- 5y+ 15 = 0 và $∆_{2} : \{\begin{cases} x = 10 - 6 t \\ y = 1 + 5 t \end{cases}$ .

A.90⁰

B.30⁰

C. 45⁰

D. 60⁰

Xem đáp án

Vectơ pháp tuyến của đường thẳng d là $n_{1} = (6; - 5)$

Vectơ pháp tuyến của đường thẳng là $∆_{2}$ =(5;6)

Ta có $n_{1} . n_{2} = 0$ => $d ⊥ ∆_{2}$

Chọn A.

Câu 21:

Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi 2 đường thẳng $∆$ ₁: x+ 2y -3= 0 và ∆₂: 2x – y + 3= 0.

A. x+ 3y-2= 0 và x= 3y.

B. 3x= - y và x-3y-6= 0.

C. 3x+ y= 0 và –x+ 3y- 6= 0.

D.Đáp án khác

Xem đáp án

Gọi M(x; y) là điểm thuộc đường phân giác tạo bởi 2 đường thẳng đã cho.

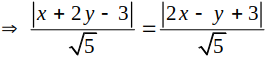
Chọn C.

Câu 22:

Cho đường thẳng d: 3x + 4y – 5= 0 và 2 điểm A( 1; 3) ; B( 2; m) . Tìm m để A và B nằm cùng phía đối với d?

A. m< 0

B. $m > - \frac{1}{4}$

C. m> 1

D. $m = - \frac{1}{4}$

Xem đáp án

Hai điểm A và B nằm về hai phía của đường thẳng d khi và chỉ khi:

( 3+ 12 -5) ( 6+ 4m -5) > 0 hay m > - $\frac{1}{4}$

Chọn B.

Câu 23:

Đường tròn (C) có tâm I( -1; 3) và tiếp xúc với đường thẳng d: 3x-4y + 5= 0 có phương trình là

A. (x+ 1) ²+ (y- 3) ²= 4.

B. (x+ 1) ²+ (y- 3) ²= 10

C. (x+ 1) ²+ (y- 3) ²= 8.

D. (x+ 1) ²+ (y- 3) ²= 16

Xem đáp án

Đường tròn có bán kính .

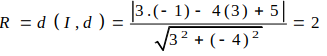
Vậy phương đường tròn là: (x+ 1) ²+ (y- 3) ²= 4.

Chọn A.

Câu 24:

Tâm của đường tròn qua ba điểm A( 2;1) ; B( 2;5) và C( -2;1) thuộc đường thẳng có phương trình

A. x- y+ 3= 0.

B. x-2 y-3= 0

C. x-y-3 = 0

D. x+ y+ 3= 0

Xem đáp án

Phương trình đường tròn (C) có dạng:

x² + y² -2ax – 2by + c= 0 ( a²+ b² –c > 0)

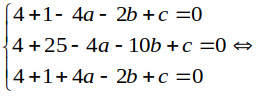
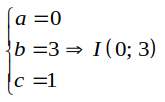
Vậy tâm đường tròn là I( 0;3) .

Lần lượt thay tọa độ I vào các phương trình đường thẳng thì chỉ có đường thẳng x- y+ 3= 0 thỏa mãn.

Chọn A.

Câu 25:

Tìm tọa độ tâm đường tròn đi qua 3 điểm A( 0;4); B( 2;4) và C( 4;0)

A. (0; 0)

B. (1; 0)

C. (3;2)

D. (1;1)

Xem đáp án

Phương trình đường tròn (C) có dạng:

x² + y² -2ax – 2by + c= 0 ( a²+ b² –c > 0)

Do 3 điểm A; B; C thuộc (C) nên

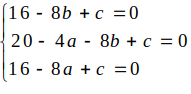
$\Leftrightarrow \{\begin{cases} a = 1 \\ b = 1 \\ c = - 8 \end{cases}$

Vậy tâm I( 1;1)

Chọn D.