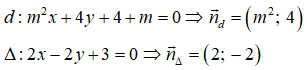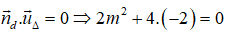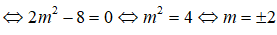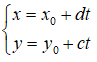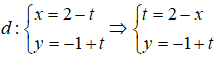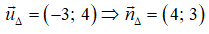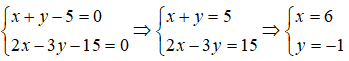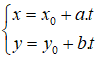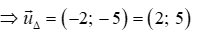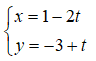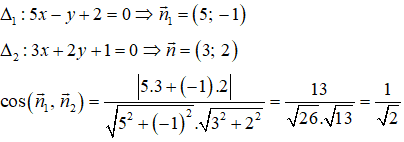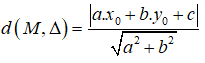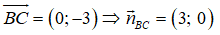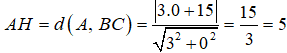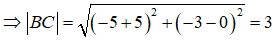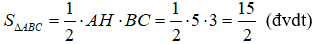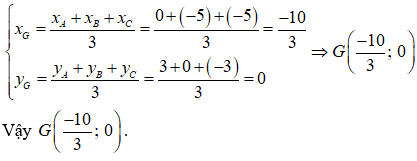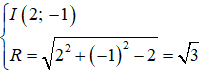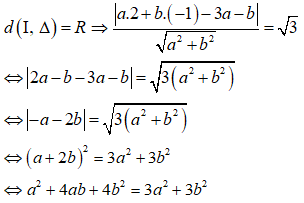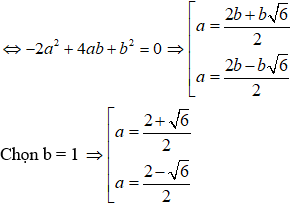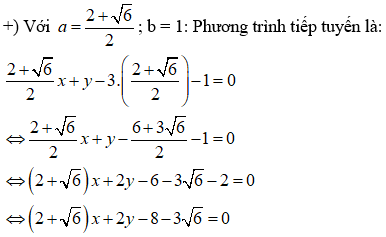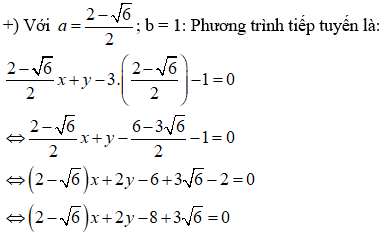16 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Hình học 10 Chương 3 có đáp án (Đề 2)

Câu 1:

Phần I: Trắc nghiệm

Tìm tham số m để hai đường thẳng d: $m^{2}$ x + 4y + 4 + m = 0 và Δ: 2x - 2y + 3 = 0 vuông góc với nhau.

A. m = 2

B. m = -2

C. m = 2 và m = -2

D. m = 4

Xem đáp án

Chọn C.

Ta có:

Để đường thẳng d và Δ vuông góc thì:

Câu 2:

Đường thẳng Δ đi qua M(x0; y0) và nhận vectơ 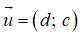làm vectơ chỉ phương có phương trình là:

A. $\{\begin{cases} x = x_{0} + d t \\ y = y_{0} + c t \end{cases}$

B. $\{\begin{cases} x = x_{0} - c t \\ y = y_{0} + d t \end{cases}$

C. $\{\begin{cases} x = x_{0} + c t \\ y = y_{0} + d t \end{cases}$

D. $\{\begin{cases} x = x_{0} + d t \\ y = y_{0} - c t \end{cases}$

Xem đáp án

Chọn A.

Phương trình tham số của đường thẳng Δ là:

Câu 3:

Cho đường thẳng $d : \{\begin{cases} x = 2 - t \\ y = - 1 + t \end{cases}$ . Phương trình tổng quát của d là:

A. x - y - 1 = 0

B. x - y + 1 = 0

C. x + y + 1 = 0

D. x + y - 1 = 0

Xem đáp án

Chọn D.

Ta có:

⇒ y = -1 + (2 - x)

⇔ y = -1 + 2 - x

⇔ -x - y + 1 = 0

⇔ x + y - 1 = 0

Vậy phương trình tổng quát của đường thẳng d là x + y - 1 = 0.

Câu 4:

Đường thẳng đi qua M(3; 2) và nhận vectơ $\vec{n} = (2; 1)$ làm vectơ pháp tuyến có phương trình tổng quát là:

A. 2x + y - 4 = 0

B. 2x + y - 8 = 0

C. x - 2y + 4 = 0

D. -2x + y - 8 = 0

Xem đáp án

Chọn B.

Phương trình tổng quát là:

2.(x - 3) + 1.(y - 2) = 0

⇒ 2x - 6 + y - 2 = 0

⇔ 2x + y - 8 = 0

Câu 5:

Vectơ nào sau đây là pháp tuyến của đường thẳng $∆ : \{\begin{cases} x = 1 - 3 t \\ y = 5 + 4 t \end{cases}$

A. $\vec{n} = (4; 3)$

B. $\vec{n} = (3; 4)$

C. $\vec{n} = (- 3; 4)$

D. $\vec{n} = (1; 5)$

Xem đáp án

Chọn A.

Ta có:

Câu 6:

Giao điểm của hai đường thẳng x + y - 5 = 0 và 2x - 3y - 15 = 0 có tọa độ là:

A. (2;3)

B. (6;-1)

C. (1;4)

D. (6;1)

Xem đáp án

Chọn B.

Tọa độ giao điểm là nghiệm của hệ phương trình:

Câu 7:

Phương trình nào sau đây biểu diễn đường thẳng không song song với đường thẳng (d): y = 2x - 1?

A. 2x - y + 5 = 0.

B. 2x - y - 5 = 0.

C. -2x + y = 0.

D. 2x + y - 5 = 0.

Xem đáp án

Chọn D.

Ta có: (d) y = 2x - 1 ⇒ (d): 2x - y - 1 = 0

Câu 8:

Vectơ $\vec{u} = (1; 2)$ là vectơ chỉ phương của đường thẳng có phương trình nào sau đây .

A. $\{\begin{cases} x = 1 + 2 t \\ y = 4 + t \end{cases}$

B. $\{\begin{cases} x = 1 + t \\ y = 4 + 2 t \end{cases}$

C. $\{\begin{cases} x = 1 - 2 t \\ y = 4 - t \end{cases}$

D. $\{\begin{cases} x = 1 + 2 t \\ y = 4 - t \end{cases}$

Xem đáp án

Chọn B.

Phương trình tham số của đường thẳng (Δ) qua một điểm có VTCP $\vec{u} = (a; b)$ có phương trình là:

Câu 9:

Đường thẳng d có một vectơ pháp tuyến là $\vec{n} = (- 2; - 5)$ . Đường thẳng Δ vuông góc với d có một vectơ chỉ phương là:

A. $\vec{u_{1}} = (5; - 2)$

B. $\vec{u_{2}} = (- 5; 2)$

C. $\vec{u_{3}} = (2; 5)$

D. $\vec{u_{4}} = (2; - 5)$

Xem đáp án

Chọn C.

Đường thẳng Δ vuông góc với d nhận VTPT của d là VTCP

Câu 10:

Phương trình tham số của đường thẳng Δ đi qua M(1;-3) và nhận vectơ $\vec{n} (1; 2)$ làm vectơ pháp tuyến.

A. $∆ : x + 2 y + 5 = 0$

B. $∆ : \{\begin{cases} x = 1 + t \\ y = - 3 + 2 t \end{cases}$

C. $∆ : \{\begin{cases} x = 1 - 2 t \\ y = - 3 + t \end{cases}$

D. $∆ : \frac{x - 1}{- 2} = \frac{y + 3}{1}$

Xem đáp án

Chọn C.

Vì Δ nhận vectơ $\vec{n} (1; 2)$ làm vectơ pháp tuyến nên VTCP của Δ là $\vec{u} (- 2; 1)$

Vậy phương trình tham số của đường thẳng Δ là

Câu 11:

Phương trình tổng quát của đường thẳng Δ biết Δ đi qua điểm M(-1;2) và có hệ số góc k=3 là:

A. 3x - y - 1 = 0

B. 3x - y - 5 = 0

C. x - 3y + 5 = 0.

D. 3x - y + 5 = 0

Xem đáp án

Chọn D.

Phương trình tổng quát của đường thẳng Δ đi qua điểm M(-1;2) và có hệ số góc k = 3 là: y = 3(x + 1) + 2 ⇔ 3x - y + 5 = 0

Câu 12:

Góc giữa hai đường thẳng Δ1: 5x - y + 2 = 0 và Δ2: 3x + 2y + 1 = 0 là:

A. 30 $°$

B. 90 $°$

C. 45 $°$

D. 0 $°$

Xem đáp án

Chọn C.

Ta có:

Vậy góc giữa hai đường thẳng Δ1, Δ2 là 45 $°$ .

Câu 13:

Khoảng cách từ điểm M(x0;y0) đường thẳng Δ: ax + by + c = 0 là:

A. $d (M, ∆) = \frac{|a . x_{0} + b . y_{0} + c|}{\sqrt{a + b}}$

B. $d (M, ∆) = \frac{|a . x_{0} + b . y_{0} + c|}{\sqrt{a^{2} + b^{2}}}$

C. $d (M, ∆) = \frac{|a . x_{0} + b . y_{0}|}{\sqrt{a^{2} + b^{2}}}$

D. $d (M, ∆) = \frac{a . x_{0} + b . y_{0} + c}{\sqrt{a^{2} + b^{2}}}$

Xem đáp án

Chọn B.

Khoảng cách từ điểm M(x0;y0)đường thẳng Δ: ax + by + c = 0 được tính theo công thức:

Câu 14:

Phương trình đường tròn (C): (x + 3 $)^{2}$ + (y + 3 $)^{2}$ = 45 có tâm và bán kính là:

A. I(-3;-3); R = 3 $\sqrt{5}$

B. I(3;3); R = 3 $\sqrt{5}$

C. I(-3;-3); R = 5 $\sqrt{3}$

D. I(3;3); R = 5 $\sqrt{3}$

Xem đáp án

Chọn A.

Phương trình đường tròn (C): (x + 3 $)^{2}$ + (y + 3 $)^{2}$ = 45

+) Tâm I(-3;-3).

+) Bán kính R = $\sqrt{45}$ = 3 $\sqrt{5}$ .

Câu 15:

Phần II: Tự luận

Trong mặt phẳng Oxy, cho ΔABC có A(0;3), B(-5;0), C(-5;-3).

a) Viết phương trình đường cao AH của ΔABC.

b) Tính diện tích và xác định tọa độ trọng tâm G của ΔABC.

Xem đáp án

a) Phương trình tổng quát của đường cao AH đi qua A(0;3) nhận 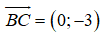làm VTPT là:

0.(x - 0) + (-3).(y - 3) = 0

⇔ -3y + 9 = 0 ⇔ 3y - 9 = 0

b)

* Tính diện tích tam giác ABC

+) Phương trình tổng quát của đường thẳng BC đi qua B(-5;0) nhận 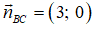là VTPT là:

3.(x + 5) + 0.(y - 0) = 0 ⇔ 3x + 15 = 0

+) Độ dài đường cao AH là khoảng cách từ A(0; 3) đến đường thẳng BC.

+) B(-5;0), C(-5;-3)

Diện tích tam giác ABC là:

* Xác định tọa độ trọng tâm G của tam giác ABC.

Tọa độ trọng tâm G(xG;yG) của tam giác ABC là:

Câu 16:

Viết phương trình tiếp tuyến kẻ từ M(3;1) đến đường tròn: (C) $x^{2}$ + $y^{2}$ - 4x + 2y + 2 = 0

Xem đáp án

* Xét đường tròn (C): $x^{2}$ + $y^{2}$ - 4x + 2y + 2 = 0

ta có:

* Phương trình đường thẳng Δ kẻ từ M(3; 1) có dạng:

a(x - 3) + b(y - 1) = 0 ⇔ ax - 3a + by - b = 0 ⇔ ax + by - 3a - b = 0

* Vì đường thẳng Δ là tiếp tuyến của đường tròn (C) nên ta có:

Vậy phương trình tiếp tuyến kẻ từ M(3;1) đến đường tròn (C): $x^{2}$ + $y^{2}$ - 4x + 2y + 2 = 0 là:

(2 + $\sqrt{6}$ )x + 2y - 8 - 3 $\sqrt{6}$ = 0 hoặc (2 - $\sqrt{6}$ )x + 2y - 8 + 3 $\sqrt{6}$ = 0