100 câu trắc nghiệm Cung và góc lượng giác nâng cao (P4)
-
9475 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 4:
Nếu 5sin α = 3sin(α + 2β) thì :
 Xem đáp án
Xem đáp án
Chọn C.
Áp dụng công thức cộng ; ta có :
5sin α = 3sin(α + 2β) ⇔ 5sin[(α + β) – β] = 3sin(α + β) + β]
⇔ 5sin(α + β)cos β – 5cos(α + β)sin β = 3sin(α + β)cos β + 3cos(α + β)sin β
⇔ 2sin(α + β)cos β = 8cos(α + β)sin β
Câu 5:
Biết và cot α, cot β, cot γ theo thứ tự lập thành một cấp số cộng. Tích số cot α.cot γ bằng :
 Xem đáp án
Xem đáp án
Chọn C.
Ta có : , suy ra
Suy ra :
( rút gọn cả 2 vế cho cotβ)
⇒ cot α.cot γ =3.
Câu 6:
Cho tam giác ABC. Hãy chọn hệ thức đúng trong các hệ thức sau.
 Xem đáp án
Xem đáp án
Chọn C.
Sử dụng công thức hạ bậc và biến đổi tổng thành tích ta có :
cos2A + cos2B + cos2C
= 1 + cos( A + B) .cos( A – B) + cos2C = 1 – cos C. cos( A – B) – cos C.cos( A + B)
= 1 – cosC[cos (A - B) + cos(A + B) ] = 1 + 2cosA. cosB.cosC
Câu 8:
Biểu thức
có kết quả rút gọn bằng
 Xem đáp án
Xem đáp án
Chọn B.
Ta có tan 460 = cot 440 và cot180 = tan 720 nên
Suy ra: B = 2 – 1 = 1.
Câu 9:
Biểu thức 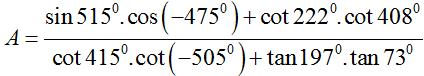 có kết quả rút gọn bằng
có kết quả rút gọn bằng
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: tan 1970 = tan170; tan 730 = cot 170; sin5150 = sin 1550; cos( -4750) = cos1150; cot2220 = cot420. Nên suy ra
Lại có; sin1550 = sin250; cos 1150 = -sin250; cot 480 = tan 420; cot ( -1450) = tan550
Câu 12:
Tính giá trị của biểu thức A = sin6x + cos6x + 3sin2x.cos2x.
 Xem đáp án
Xem đáp án
Chọn B.
Ta có A = sin6x + cos6x + 3sin2x.cos2x.
= ( sin2x)3 + (cos2x)3 + 3sin2x.cos2x.
= (sin2x + cos2x)3 - 3sin2x.cos2x(sin2x + cos2x) + 3.sin2x.cos2x
= 1 - 3.sin2x.cos2x + 3.sin2x.cos2x = 1
Câu 15:
Rút gọn biểu thức C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x)
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
C = [ ( sin2x + cos2x) – sin2cos2x]2 - [ ( sin4x + cos4x) 2 - 2sin4x.cos4x]
= 2[ 1-sin2x.cos2x]2 - [ ( sin2x + cos2x) 2 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2[ 1-sin2x.cos2x]2 - [1-sin2x.cos2x]2 + 2sin4x.cos4x
= 2( 1 - 2sin2x.cos2x + sin4x.cos4x)- ( 1 - 4sin2xcos2x + 4sin4x.cos4x) + 2sin4x.cos4x
= 1.
Câu 16:
Hệ thức nào sai trong bốn hệ thức sau:
 Xem đáp án
Xem đáp án
Chọn D.
Ta xét các đáp án.
+ A đúng vì
+ B đúng vì
+ C đúng vì
Câu 17:
Nếu biết 3.sin4x + 2cos4x = 98/81 thì giá trị biểu thức A = 2sin4x + 3cos4x bằng
 Xem đáp án
Xem đáp án
Chọn D.
Ta có
Đặt
Câu 18:
Nếu sinx + cosx = 1/2 thì 3sinx + 2cosx bằng
 Xem đáp án
Xem đáp án
Chọn A.
Ta có:
sinx + cosx = ½ nên ( sinx + cosx)2 = ¼
Do đó sinx. cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
Ta có sinx + cos x = ½ nên 2( sinx + cosx) = 13sinx+2cosx = sinx+2(sinx+cosx)=sinx+1
+) Với
+) Với
Câu 19:
Biết . Giá trị của biểu thức A = a.cos2x + 2b.sinx.cosx + c.sin2x bằng
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: A = a.cos2x + 2b.sinx.cosx + c.sin2x
Hay A( 1 + tan2x) = a + 2btanx + c.tan2x
Do đó: A = a.
Câu 20:
Nếu biết thì biểu thức
bằng
 Xem đáp án
Xem đáp án
Chọn C.
Đặt
Hay
Suy ra:
Quy đồng khử mẫu ta được:
(a + b) 2t2 - 2b( a + b)t + b2 = 0
Suy ra
Vậy:
Câu 24:
Cho tam giác ABC và các mệnh đề :
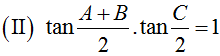
(III): cos(A + B - C) – cos 2C=0
Mệnh đề đúng là :
 Xem đáp án
Xem đáp án
Chọn C.
+) Ta có:
nên (I) đúng
+) Tương tự ta có:
nên (II) đúng.
+) Ta có
A + B – C = π – 2C → cos(A + B + C) = cos(π – 2C) = -cos2C
⇔ cos(A + B – C) - cos(2C) = -2cos2C
nên (III) sai.

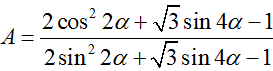
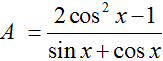
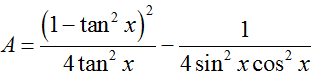
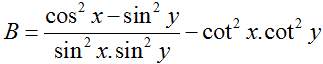
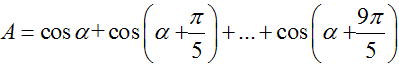
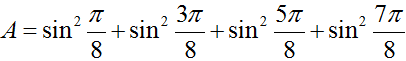 bằng
bằng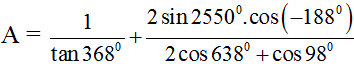 bằng :
bằng :