15 câu trắc nghiệm Toán 9 Chân trời sáng tạo Bài 2. Tiếp tuyến của đường tròn có đáp án
15 câu trắc nghiệm Toán 9 Chân trời sáng tạo Bài 2. Tiếp tuyến của đường tròn có đáp án
-
37 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đường thẳng và đường tròn có nhiều nhất 2 điểm chung.
Vậy ta chọn phương án B.
Câu 2:
Cho đường tròn \[\left( O \right)\] và đường thẳng \[a.\] Kẻ \[OH \bot a\] tại điểm \[H,\] biết \[OH > R.\] Khi đó, đường thẳng \[a\] và đường tròn \[\left( O \right)\] có vị trí tương đối là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Vì \[OH > R\] nên đường thẳng \[a\] và đường tròn \[\left( O \right)\] không cắt nhau.
Vậy ta chọn phương án C.
Câu 3:
Cho đường tròn \[\left( O \right)\] và đường thẳng \[a.\] Kẻ \[OH \bot a\] tại điểm \[H,\] biết \[OH < R.\] Khi đó, đường thẳng \[a\] và đường tròn \[\left( O \right)\]
</>
 Xem đáp án
Xem đáp án
Đáp án đúng là: B

Vì \[OH < R\] nên đường thẳng \[a\] và đường tròn \[\left( O \right)\] cắt nhau.
Vậy ta chọn phương án B.
Câu 4:
Cho đường tròn \[\left( O \right)\] và điểm \[A\] nằm trên đường tròn \[\left( O \right).\] Nếu đường thẳng \[d \bot OA\] tại \[A\] thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: A

Vì đường thẳng \[d\] đi qua điểm \[A\] nằm trên đường tròn \[\left( O \right)\] và vuông góc với bán kính \[OA\] của đường tròn \[\left( O \right)\] nên đường thẳng \[d\] là một tiếp tuyến của đường tròn \[\left( O \right).\]
Tức là, \[d\] là tiếp tuyến của \[\left( O \right),\] với \[A\] là tiếp điểm.
Vậy ta chọn phương án A.
Câu 5:
Cho hai tiếp tuyến của đường tròn cắt nhau tại một điểm. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hai tiếp tuyến đường tròn cắt nhau tại một điểm thì:
⦁ Khoảng cách từ điểm đó đến hai tiếp điểm bằng nhau
⦁ Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
⦁ Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi hai bán kính.
Vậy phương án A là khẳng định đúng, ta chọn phương án A.
Câu 6:
II. Thông hiểu
Cho \[a\] và \[b\] là hai đường thẳng song song và cách nhau một khoảng bằng \[3{\rm{\;cm}}.\] Lấy điểm \[I\] trên \[a\] và vẽ đường tròn \[\left( {I;3,5{\rm{\;cm}}} \right).\] Khi đó đường tròn \[\left( I \right)\] với đường thẳng \[b\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: A

Kẻ \[IH \bot b\] tại \[H.\]
Vì \[a\] và \[b\] là hai đường thẳng song song và cách nhau một khoảng bằng \[3{\rm{\;cm}}\] và \[I \in a\] nên khoảng cách từ tâm \[I\] đến đường thẳng \[b\] là \[IH = 3{\rm{\;(cm)}}{\rm{.}}\]
Do \[IH = 3{\rm{\;cm}} < R = 3,5{\rm{\;cm}}\] nên đường tròn \[\left( I \right)\] với đường thẳng \[b\] cắt nhau.
Vậy ta chọn phương án A.
Câu 7:
Cho \[a\] và \[b\] là hai đường thẳng song song và cách nhau một khoảng bằng \[2,5{\rm{\;cm}}.\] Lấy điểm \[I\] trên \[a\] và vẽ đường tròn \[\left( {I;2,5{\rm{\;cm}}} \right).\] Khi đó đường tròn \[\left( I \right)\] với đường thẳng \[b\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: B

Kẻ \[IH \bot b\] tại \[H.\]
Vì \[a\] và \[b\] là hai đường thẳng song song và cách nhau một khoảng bằng \[2,5{\rm{\;cm}}\] và \[I \in a\] nên khoảng cách từ tâm \[I\] đến đường thẳng \[b\] là \[IH = 2,5{\rm{\;(cm)}}{\rm{.}}\]
Do \[IH = R = 2,5{\rm{\;(cm)}}\] nên đường tròn \[\left( I \right)\] với đường thẳng \[b\] tiếp xúc nhau tại tiếp điểm \[H.\]
Vậy ta chọn phương án B.
Câu 8:
Cho bảng sau với \[R\] là bán kính của đường tròn, \[d\] là khoảng cách từ tâm đến đường thẳng:
|
\[R\] |
\[d\] |
Vị trí tương đối của đường thẳng và đường tròn |
|
5 cm |
4 cm |
(1) |
|
8 cm |
(2) |
Tiếp xúc nhau |
Điền vào các vị trí (1), (2) trong bảng trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
⦁ Vì \[4{\rm{\;cm}} < 5{\rm{\;cm}}\] nên \[d < R.\] Suy ra đường thẳng cắt đường tròn.
⦁ Vì đường thẳng tiếp xúc với đường tròn nên \[d = R.\] Suy ra \[d = 8{\rm{\;cm}}.\]
Do đó ở vị trí (1) ta điền “Cắt nhau”; ở vị trí (2) ta điền “8 cm”.
Vậy ta chọn phương án A.
Câu 9:
Cho đường thẳng \[d\] và một điểm \[I\] cách \[d\] một khoảng bằng 10 cm. Vẽ đường tròn \[\left( I \right)\] đường kính 18 cm. Khi đó đường thẳng \[d\] và đường tròn \[\left( I \right)\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
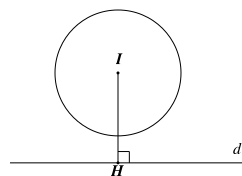
Kẻ \[IH \bot d\] tại \[H.\] Suy ra \[IH = 10{\rm{\;(cm)}}{\rm{.}}\]
Bán kính của đường tròn \[\left( I \right)\] là: \[R = \frac{{18}}{2} = 9{\rm{\;(cm)}}{\rm{.}}\]
Vì \[10{\rm{\;cm}} > 9{\rm{\;cm}}\] nên \[IH > R.\]
Do đó đường thẳng \[d\] và đường tròn \[\left( I \right)\] không giao nhau.
Vậy ta chọn phương án C.
Câu 10:
Hai tiếp tuyến tại \[B\] và \[C\] của đường tròn \[\left( {O;R} \right)\] cắt nhau tại \[A.\] Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
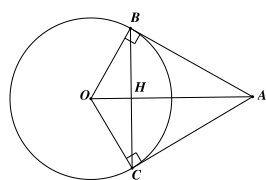
Gọi \[H\] là giao điểm của \[BC\] và \[OA.\]
Xét đường tròn \[\left( O \right)\] có hai tiếp tuyến tại \[B\] và \[C\] cắt nhau tại \[A\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[AB = AC.\] Do đó điểm \[A\] nằm trên đường trung trực của đoạn \[BC\] (1)
Đường tròn \[\left( O \right)\] có \[OB = OC = R\] nên điểm \[O\] nằm trên đường trung trực của đoạn \[BC\] (2)
Từ (1), (2), ta thu được \[OA\] là đường trung trực của đoạn \[BC.\]
Suy ra \[OA \bot BC\] tại \[H\] là trung điểm của \[BC.\]
Do đó ta chưa kết luận được \[H\] có là trung điểm của \[OA\] hay không.
Vì vậy phương án A, B, C đúng và phương án D sai.
Vậy ta chọn phương án D.
Câu 11:
Cho điểm \[M\] nằm ngoài đường tròn \[\left( I \right)\] và \[ME,MF\] là hai tiếp tuyến của đường tròn này tại \[E,F.\] Cho biết \[\widehat {EMF} = 60^\circ .\] Tam giác \[EMF\] là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
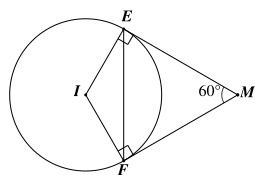
Vì \[ME,MF\] là hai tiếp tuyến của đường tròn \[\left( I \right)\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[ME = MF.\] Do đó tam giác \[EMF\] cân tại \[M.\]
Mà \[\widehat {EMF} = 60^\circ \] nên tam giác \[EMF\] đều.
Vậy ta chọn phương án C.
Câu 12:
Cho đường tròn \[\left( O \right)\] đường kính \[AD.\] Vẽ tiếp tuyến \[AC\] tại \[A\] của đường tròn, từ \[C\] trên tiếp tuyến đó vẽ tiếp tuyến thứ hai \[CM\] của đường tròn \[\left( O \right)\] (\[M\] là tiếp điểm và \[M\] khác \[A\]) cắt \[AD\] tại \[B.\] Giả sử \[AC = 6{\rm{\;cm}},AB = 8{\rm{\;cm}}.\] Độ dài \[BM\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
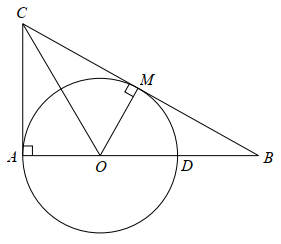
Vì \[AC\] là tiếp tuyến của đường tròn \[\left( O \right)\] nên \[AC \bot AO\] tại \[A.\]
Áp dụng định lí Pythagore cho tam giác \[ABC\] vuông tại \[A,\] ta được:
\[B{C^2} = A{B^2} + A{C^2} = {8^2} + {6^2} = 100.\] Suy ra \[BC = 10{\rm{\;(cm)}}{\rm{.}}\]
Vì \[AC,\,\,CM\] là hai tiếp tuyến của đường tròn \[\left( O \right)\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[CM = CA = 6{\rm{\;(cm)}}{\rm{.}}\]
Ta có \[BM = BC - CM = 10 - 6 = 4{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 13:
III. Vận dụng
Cho đường tròn \[\left( {O;R} \right)\] và dây \[AB = 1,2R.\] Vẽ đường thẳng tiếp xúc với \[\left( {O;R} \right)\] và song song với \[AB,\] cắt các tia \[OA,OB\] lần lượt tại \[E\] và \[F.\] Diện tích tam giác \[OEF\] theo \[R\] là
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Đáp án đúng là: A
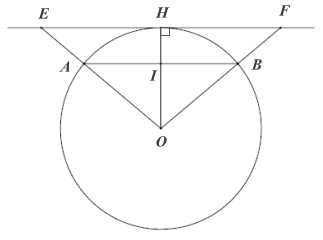
Giả sử đường thẳng \[EF\] tiếp xúc với đường tròn \[\left( O \right)\] tại \[H.\] Khi đó \[OH \bot EF.\]
Gọi \[I\] là giao điểm của \[OH\] và \[AB.\]
Vì \[EF\,{\rm{//}}\,AB\] nên \[OH \bot AB.\]
Vì tam giác \[OAB\] cân tại \[O\] (do \[OA = OB = R\]) nên \[OI\] vừa là đường cao, vừa là đường trung tuyến của tam giác. Do đó \[I\] là trung điểm \[AB.\]
Vì vậy \[IA = IB = \frac{{AB}}{2} = \frac{{1,2R}}{2} = 0,6R.\]
Áp dụng định lí Pythagore cho tam giác \[OAI\] vuông tại \[I,\] ta được: \[O{A^2} = O{I^2} + A{I^2}.\]
Suy ra \[O{I^2} = O{A^2} - A{I^2} = {R^2} - {\left( {0,6R} \right)^2} = 0,64{R^2}.\]
Do đó \[OI = 0,8R.\]
Vì \[AI\,{\rm{//}}\,EH\] nên áp dụng định lí Thales, ta có \[\frac{{AI}}{{EH}} = \frac{{OI}}{{OH}}.\]
Suy ra \[\frac{{0,6R}}{{EH}} = \frac{{0,8R}}{R}.\]
Do đó \[EH = 0,75R.\]
Vì \[AB\,{\rm{//}}\,EF\] nên \[\widehat {OAB} = \widehat {OEF}\] (cặp góc đồng vị).
Chứng minh tương tự, ta được \[\widehat {OBA} = \widehat {OFE}.\]
Mà \[\widehat {OBA} = \widehat {OAB}\] (do tam giác \[OAB\] cân tại \[O\]).
Do đó \[\widehat {OEF} = \widehat {OFE}.\] Vì vậy tam giác \[OEF\] cân tại \[O.\]
Tam giác \[OEF\] cân tại \[O\] có \[OH\] là đường cao nên \[OH\] cũng là đường trung tuyến của tam giác.
Do đó \[H\] là trung điểm \[EF.\]
Vì vậy \[EF = 2EH = 2 \cdot 0,75R = 1,5R.\]
Diện tích tam giác \[OEF\] là: \[{S_{OEF}} = \frac{1}{2} \cdot OH \cdot EF = \frac{1}{2} \cdot R \cdot 1,5R = 0,75{R^2}.\]
Vậy ta chọn phương án A.
Câu 14:
Cho đường tròn \[\left( O \right),\] từ một điểm \[M\] ở ngoài \[\left( O \right),\] vẽ hai tiếp tuyến \[MA\] và \[MB\] sao cho \[\widehat {AMB}\] bằng \[120^\circ .\] Biết chu vi tam giác \[MAB\] là \[6\left( {3 + 2\sqrt 3 } \right){\rm{\;cm}}.\] Khi đó độ dài dây \[AB\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
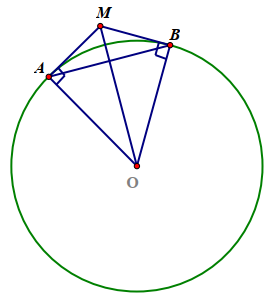
Ta có \[MA,MB\] là hai tiếp tuyến của \[\left( O \right)\] cắt nhau tại \(M\) nên \[MA = MB\] và \[MO,\,\,OM\] lần lượt là tia phân giác của \[\widehat {AMB},\,\,\widehat {AOB}.\]
Khi đó \[\widehat {AMO} = \widehat {OMB} = \frac{{\widehat {AMB}}}{2} = \frac{{120^\circ }}{2} = 60^\circ .\]
Ta có \[MA\] là tiếp tuyến của \[\left( O \right)\] nên \[MA \bot OA\] tại \[A.\]
Vì tam giác \[OAM\] vuông tại \[A\] nên \[AM = AO \cdot \cot \widehat {AMO} = R \cdot \cot 60^\circ = \frac{{R\sqrt 3 }}{3}.\]
Suy ra \[MB = MA = \frac{{R\sqrt 3 }}{3}.\]
Vì tam giác \[OAM\] vuông tại \[A\] nên \[\widehat {AMO} + \widehat {AOM} = 90^\circ .\]
Suy ra \[\widehat {AOM} = 90^\circ - \widehat {AMO} = 90^\circ - 60^\circ = 30^\circ .\]
Ta có \[OM\] là tia phân giác của \[\widehat {AOB}\] nên \[\widehat {AOB} = 2\widehat {AOM} = 2 \cdot 30^\circ = 60^\circ .\]
Xét tam giác \[OAB\] có \[OA = OB = R\] và \[\widehat {AOB} = 60^\circ \] nên tam giác \[OAB\] là tam giác đều.
Khi đó \[AB = OA = OB = R.\]
Ta có chu vi tam giác \[MAB\] là \(MA + MB + AB\)
Theo bài chu vi tam giác \[MAB\] bằng \[6\left( {3 + 2\sqrt 3 } \right){\rm{\;cm,}}\] suy ra:
\[\frac{{R\sqrt 3 }}{3} + \frac{{R\sqrt 3 }}{3} + R = 6\left( {3 + 2\sqrt 3 } \right)\,\]
\[R \cdot \left( {\frac{{2\sqrt 3 + 3}}{3}} \right) = 6\left( {3 + 2\sqrt 3 } \right)\]
\[R = 18{\rm{\;(cm)}}{\rm{.}}\]
Vì vậy \[AB = R = 18{\rm{\;(cm)}}{\rm{.}}\] Vậy ta chọn phương án C.
Câu 15:
Một thủy thủ đang ở trên cột buồm của một con tàu, cách mặt nước biển \[10{\rm{\;m}}.\] Biết bán kính Trái Đất là khoảng \[6\,\,400{\rm{\;km}}.\] Tầm nhìn xa tối đa (làm tròn kết quả đến hàng phần nghìn của km) của thủy thủ đó bằng khoảng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
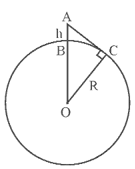
Đổi: \[10{\rm{\;m}} = 0,01{\rm{\;km}}.\]
Gọi \[O\] là tâm Trái Đất và \[R\] là bán kính Trái Đất. Suy ra \[R = 6400{\rm{\;km}}.\]
Ta có điểm \[B\] biểu diễn vị trí con tàu và điểm \[A\] biểu diễn vị trí của thủy thủ.
Suy ra \[h = AB = 10{\rm{\;(m)}}{\rm{.}}\]
Lại có điểm \[A\] biểu diễn vị trí của thủy thủ và điểm \[C\] biểu diễn điểm xa nhất mà thủy thủ nhìn thấy. Khi đó độ dài đoạn \[AC\] gọi là tầm nhìn xa tối đa từ điểm \[A.\]
Vì \[AC\] là tiếp tuyến của đường tròn \[\left( {O;R} \right)\] tại \[C\] nên \[AC \bot OC\] tại \[C.\]
Áp dụng định lí Pythagore cho tam giác \[AOC\] vuông tại \[C,\] ta được: \[O{A^2} = A{C^2} + O{C^2}.\]
Suy ra \[A{C^2} = O{A^2} - O{C^2} = {\left( {OB + AB} \right)^2} - O{C^2}\]
\[A{C^2} = {\left( {R + h} \right)^2} - {R^2} = {\left( {6\,\,400 + 0,01} \right)^2} - 6\,\,{400^2} = 128,0001.\]
Khi đó \[AC \approx 11,314{\rm{\;(km)}}{\rm{.}}\]
Do đó tầm nhìn xa tối đa của thủy thủ đó bằng khoảng \[11,314{\rm{\;km}}.\]
Vậy ta chọn phương án D.
