Bài tập theo tuần Toán 9 - Tuần 1
-
1677 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A, AH là đường cao, biết rằng AB = 6cm, AC = 8cm. Tính BH, CH.
 Xem đáp án
Xem đáp án
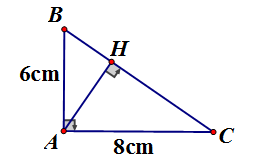
Áp dụng hệ thức lượng vào vuông , đường cao AH ta có:
Áp dụng định lý Pytago vào
Áp dụng định lý Pytago vào vuông tại H
Vậy
Câu 2:
 Xem đáp án
Xem đáp án
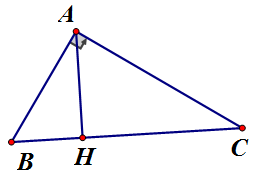
Ta có: ;
vuông tại A (định lý Pytago đảo)
Áp dụng hệ thức lượng vào vuông tại A, đường cao AH
. Vậy .
Câu 3:
Cho nhọn, BD, CE là hai đường cao. Các điểm N, M trên các đường thẳng BD, CE sao cho Chứng minh cân
 Xem đáp án
Xem đáp án
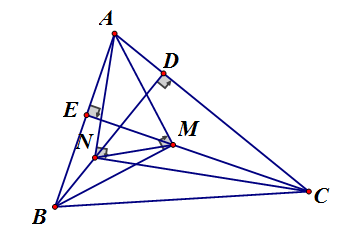
vuông tại N, có ND là đường cao, áp dụng hệ thức lượng trong tam giác vuông, ta có:
Chứng minh tương tự trong vuông
Xét và có chung;
(hai cặp cạnh tương ứng tỉ lệ)
Từ (1), (2), (3) cân tại A
Câu 4:
Cho hình vuông ABCD một điểm E bất kỳ thuộc cạnh AB. Gọi F là giao điểm của DE và BC. Chứng minh rằng:
 Xem đáp án
Xem đáp án
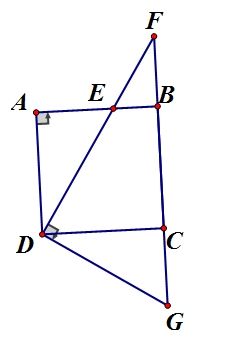
Vẽ . Xét vuông tại A và vuông tại C có:
(cùng phụ
vuông tại D, DC là đường cao nên áp dụng hệ thức lượng ta có:
mà DG = DE (cmt), DC = DA (tính chất hình vuông)
