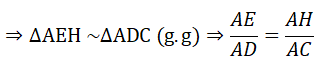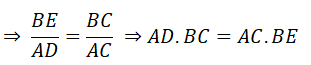12 câu hỏi trắc nghiệm thuộc Đề kiểm tra 1 tiết Toán 9 Chương 3 Hình học có đáp án (Đề 1)

Đề kiểm tra 1 tiết Toán 9 Chương 3 Hình học có đáp án

Đề kiểm tra 1 tiết Toán 9 Chương 3 Hình học có đáp án (Đề 1)

1202 lượt thi
12 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phần trắc nghiệm

Nội dung câu hỏi 1

Trong một đường tròn:

A. Các góc nội tiếp bằng nhau thì chắn một cung

B. Số đo của góc ở tâm bằng số đo của góc nội tiếp cùng chắn một cung

C. Góc nội tiếp chắn nửa đường tròn là góc vuông

D. Góc có 2 cạnh chứa 2 dây của đường tròn là góc nội tiếp

Xem đáp án

Đáp án là C

Câu 2:

Biết diện tích hình tròn là 64π ( $c m^{2}$ ) . Chu vi hình tròn này bằng:

A. 12π (cm)

B. 16π (cm)

C. 15π (cm)

D. 20π (cm)

Xem đáp án

Đáp án là B

S = π $R^{2}$ = 64π ⇒ R = 8

Chu vi hình tròn là: C = 2πR = 2π.8 = 16π cm

Câu 3:

Cho đường tròn O và góc nội tiếp ∠BAC = $50^{0}$ . Số đo độ của cung nhỏ BC bằng:

A. $50^{0}$

B. $60^{0}$

C. $70^{0}$

D. $100^{0}$

Xem đáp án

Đáp án là D

Câu 4:

Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. Các tứ giác nào sau đây nội tiếp được đường tròn.

A.AEHF

B. BFEC

C. AEDB

D. Cả A, B, C.

Xem đáp án

Đáp án là C

Câu 5:

Cho tứ giác ABCD nội tiếp đường tròn (O). Hai cạnh đối AB và CD cắt nhau tại một điểm M ở ngoài (O), biết ∠BAD = $60^{0}$ thì góc BMC bằng:

A. $120^{0}$

B. $60^{0}$

C. $90^{0}$

D. $30^{0}$

Xem đáp án

Đáp án là A

Câu 6:

Qũy tích các điểm M nhìn đoạn thẳng AB dưới một góc $120^{0}$ là:

A. Một đường tròn đi qua hai điểm A, B

B. Một đường thẳng song song với AB

C. Một cung chứa góc $120^{0}$ dựng trên hai điểm A, B

D. Hai cung chứa góc $120^{0}$ (đối xứng nhau) dựng trên hai điểm A, B.

Xem đáp án

Đáp án là D

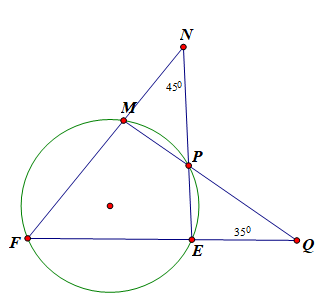
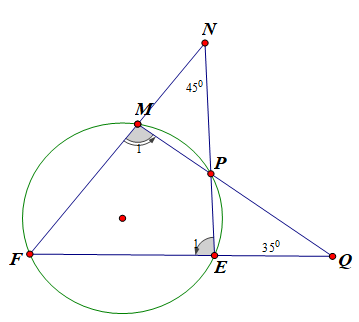
Câu 7:

Cho hình vẽ, biết ∠(EQM) = $35^{0}$ ; ∠(FNE) = $45^{0}$ . Tính số đo ∠(NFQ)

A. $50^{0}$

B. $80^{0}$

C. $100^{0}$

D. Không xác định được

Xem đáp án

Đáp án là A

Xét tam giác NEF có: ∠F + ∠N + ∠ $E_{1}$ = $180^{0}$ ⇒ ∠F + ∠E1 = $135^{0}$

Xét tam giác FQM có: ∠F + ∠Q + ∠M1 = $180^{0}$ ⇒ ∠F + ∠M1 = $145^{0}$

Do FMPE là tứ giác nội tiếp nên ∠E1 + ∠M1 = $180^{0}$

Do đó ta có: 2∠F + $180^{0}$ = $280^{0}$ ⇒ ∠F = $50^{0}$

Câu 8:

Độ dài của cung $45^{0}$ của đường tròn có bán kính là 5 cm

A. 3π/8 cm

B. 5π/8 cm

C. π/2 cm

D. π cm

Xem đáp án

Đáp án là B

Câu 9:

Phần tự luận

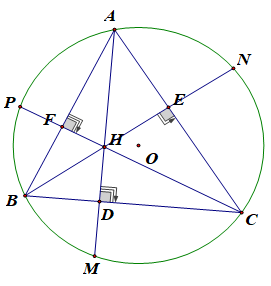
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:

a) Tứ giác CEHD nội tiếp

Xem đáp án

a) Xét tứ giác CEHD có:

∠(CED) = $90^{0}$ (do BE là đường cao)

∠(HDC) = $90^{0}$ (do AD là đường cao)

⇒ ∠(CED) + ∠(HDC) = $180^{0}$

Mà ∠(CED) và ∠(HDC) là 2 góc đối của tứ giác CEHD nên CEHD là tứ giác nội tiếp

Câu 10:

Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:

b) Bốn điểm B, C, E, F cùng nằm trên một đường tròn

Xem đáp án

b) Xét tứ giác BFEC có:

∠(BFC) = $90^{0}$ (Do CF là đường cao)

∠(BEC ) = $90^{0}$ (Do BE là đường cao)

⇒ E và F cùng nhìn BC dưới một góc bằng nhau

⇒ Tứ giác BFEC nội tiếp được đường tròn

⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn

Câu 11:

Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:

c) AE.AC = AH.AD ; AD.BC = BE.AC

Xem đáp án

c) Xét ΔAEH và ΔADC có:

∠(AEH) = ∠(ADC) = $90^{0}$

∠(DAC) là góc chung

⇒ AE.AC = AD.AH

Xét Δ BEC và ΔADC có:

∠(BEC) = ∠(ADC) = $90^{0}$

∠(ACD) là góc chung

⇒ ΔBEC ∼ ΔADC (g.g)

Câu 12:

Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:

d) H và M đối xứng nhau qua BC

Xem đáp án

d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)

Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)

Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)

Mặt khác, ta có: ∠( $A_{1}$ ) = ∠( $C_{2}$ ) ( 2 góc nội tiếp cùng chắn cung BM)

⇒ ∠( $C_{1}$ ) = ∠( $C_{2}$ )

⇒ CD là tia phân giác của góc HCM

Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)

⇒ Δ HCM cân tại C

⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.

Bắt đầu thi ngay