Đáp án đúng là: B

Đường tròn ngoại tiếp đa giác là đường tròn đi qua tất cả các đỉnh của đa giác đó.

Đáp án đúng là: B

Tâm đường tròn nội tiếp của một tam giác là giao của các đường phân giác trong của tam giác đó.

Đáp án đúng là: A

Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực của tam giác đó.

Đáp án đúng là: C

Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn ngoại tiếp nên đáp án A và B đều đúng.

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của một tam giác nên đáp án D không đúng.

Vậy đáp án đúng nhất là đáp án C.

Đáp án đúng là: B

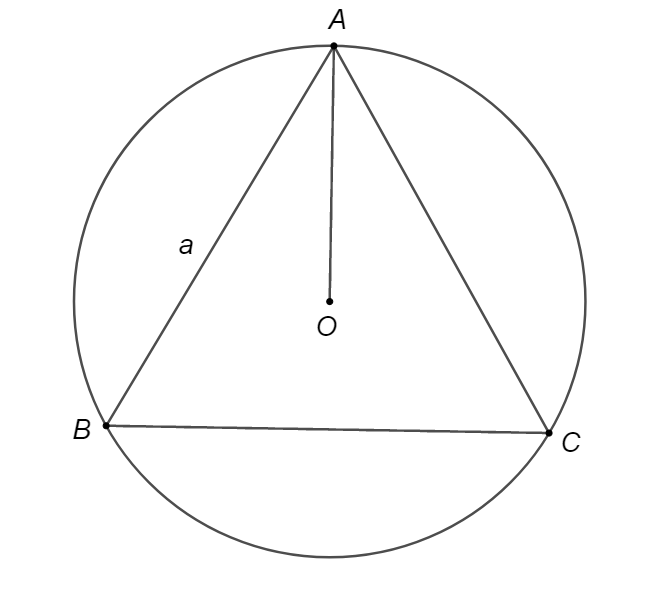
Đường tròn ngoại tiếp tam giác đều cạnh 

Đáp án đúng là: C

Gọi \[O\] là tâm của hình vuông \[ABCD\].

Gọi \[E;{\rm{ }}F;{\rm{ }}K;{\rm{ }}G\] lần lượt là trung điểm của \[AD,{\rm{ }}DC,{\rm{ }}BC,{\rm{ }}AB\].

Khi đó ta có \[OE = OF = OK = OG = \;\frac{a}{2}\] hay \[O\] là tâm đường tròn nội tiếp hình vuông \[ABCD\].

Vậy bán kính đường tròn nội tiếp hình vuông là \(R = \frac{a}{2}\).

Đáp án đúng là: B

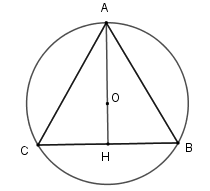
Gọi tam giác đều \[ABC\] nội tiếp đường tròn \[\left( {O;{\rm{ }}R} \right)\] có cạnh là \[a.\]

Khi đó \[O\] là trọng tâm tam giác \[ABC\].

Gọi \[AH\] là đường trung tuyến.

Suy ra \(R = AO = \frac{2}{3}AH\) hay \(AH = \frac{{3R}}{2}\).

Áp dụng định lý Pythagore với tam giác \[ABH\] vuông tại \[H\], ta có: \(A{H^2} = A{B^2} - B{H^2}.\)

Khi đó \[AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\].

Do đó \(\frac{{3R}}{2} = \frac{{a\sqrt 3 }}{2}\) hay \(a = R\sqrt 3 \).

Đáp án đúng là: D

Gọi tam giác đều \[ABC\] nội tiếp đường tròn \[\left( {O;{\rm{ }}R} \right)\] có cạnh là \[a\].

Khi đó \[O\] là trọng tâm tam giác \[ABC\] và cũng là tâm đường tròn ngoại tiếp tam giác \[ABC\] nên \(AO = 2\,\,{\rm{cm}}\).

Gọi \[AH\] là đường trung tuyến.

Suy ra \(2 = AO = \frac{2}{3}AH\) hay \(AH = 3\,\,{\rm{cm}}\).

Áp dụng định lý Pythagore với tam giác \[ABH\] vuông tại \[H\], ta có: \(A{H^2} = A{B^2} - B{H^2}.\)

Khi đó \[AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\].

Do đó \(3 = \frac{{a\sqrt 3 }}{2}\) hay \(a = 2\sqrt 3 \) (cm).

Diện tích tam giác \[ABC\] là: \(\frac{1}{2}AH \cdot BC = \frac{1}{2} \cdot 2 \cdot 2\sqrt 3 = 3\sqrt 3 \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\) .

Vậy diện tích tam giác đều nội tiếp đường tròn \(\left( {O\,;\,\,2\,\,{\rm{cm}}} \right)\) là \(3\sqrt 3 \,\,{\rm{c}}{{\rm{m}}^2}\).

Đáp án đúng là: C

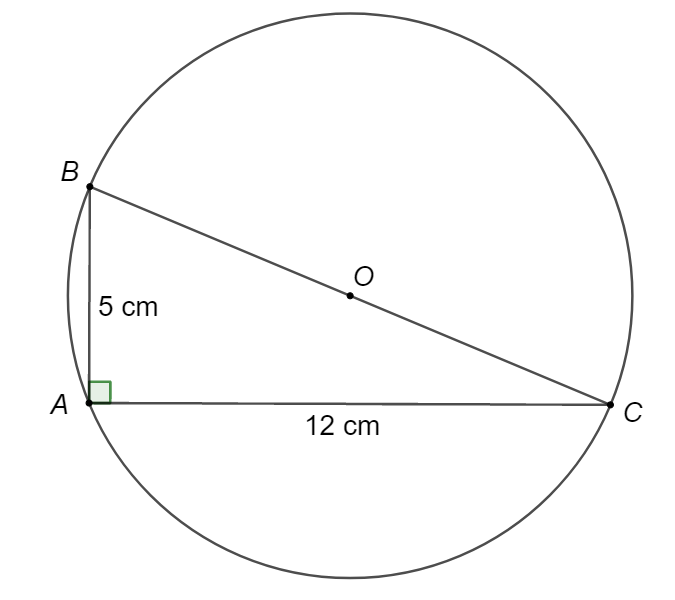
Vì tam giác \[ABC\] vuông tại \[A\] nên tâm đường tròn ngoại tiếp là trung điểm O của cạnh huyền \[BC\], bán kính \(R = \frac{{BC}}{2}\).

Theo định lý Pythagore, ta có: \(BC = \sqrt {A{C^2} + A{B^2}} = \sqrt {{5^2} + {{12}^2}} = 13\) (cm).

Vậy bán kính đường tròn ngoại tiếp tam giác \[ABC\] là \(R = \frac{{BC}}{2} = \frac{{13}}{2}\) (cm).

Đáp án đúng là: D

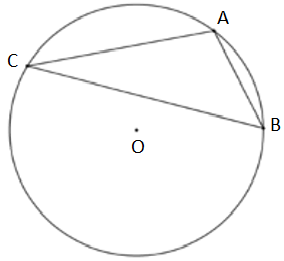
Vì \[AC\] bằng cạnh của hình vuông nội tiếp \[\left( O \right)\] nên số đo cung \[AC = 90^\circ \].

Vì \[BC\] bằng cạnh của tam giác đều nội tiếp \[\left( O \right)\] nên số đo cung \[BC = 120^\circ \].

Từ đó suy ra số đo cung \[AB\] bằng \[120^\circ --90^\circ = 30^\circ \].

Vì góc \[ACB\] là góc nội tiếp chắn cung \[AB\] nên \(\widehat {ACB} = \frac{{30^\circ }}{2} = 15^\circ \).

Vậy \(\widehat {ACB} = 15^\circ \).

Đáp án đúng là: B

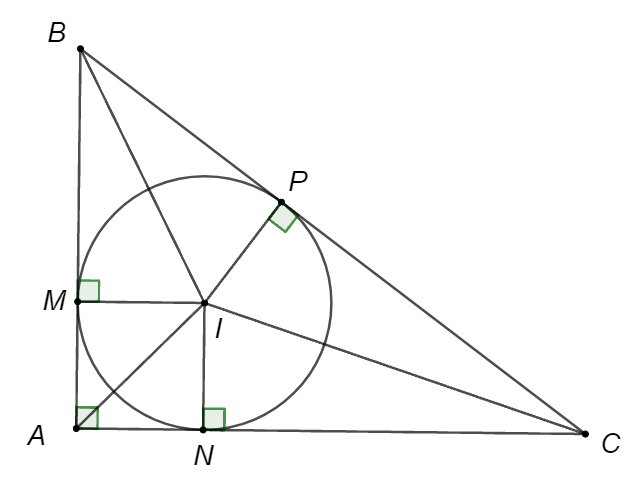
Đường tròn \[\left( {I;{\rm{ }}r} \right)\] tiếp xúc với các cạnh \[AB,{\rm{ }}AC,{\rm{ }}BC\] theo thứ tự \[M,{\rm{ }}N,{\rm{ }}P\].

Ta có: \({S_{AIB}} = \frac{1}{2}IM \cdot AB = \frac{1}{2} \cdot r \cdot AB & \left( 1 \right)\)

\({S_{AIC}} = \frac{1}{2}IN \cdot AC = \frac{1}{2} \cdot r \cdot AC & \left( 2 \right)\)

\({S_{BIC}} = \frac{1}{2}r.BC & & & \left( 3 \right)\)

Cộng vế theo vế ở các biểu thức \(\left( 1 \right),\,\,\left( 2 \right),\,\,\left( 3 \right)\), ta được:

\(\frac{{{S_{AIB}} + {S_{AIC}} + {S_{BIC}}}}{{{S_{ABC}}}} = \frac{1}{2}r\left( {AB + AC + BC} \right)\).

Mà \({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.6.8 = 24\) (cm²), \(BC = \sqrt {{6^2} + {8^2}} = 10\) (cm)

Nên ta có: \(24 = \frac{1}{2}r \cdot \left( {6 + 8 + 10} \right)\) hay \(\frac{1}{2}r \cdot 12 = 24\).

Do đó \(r = 2\,\,{\rm{cm}}\).

Đáp án đúng là: B

A.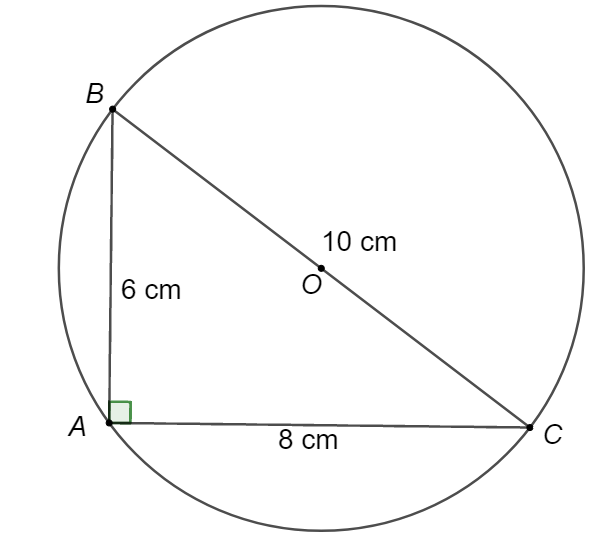

Ta có: \[A{B^2} + A{C^2} = B{C^2}\left( { = 100} \right)\] .

Suy ra tam giác \[ABC\] vuông tại \[A\].

Do đó, tâm đường tròn ngoại tiếp tam giác \[ABC\] là trung điểm O của cạnh huyền \[BC\].

Đường kính đường tròn là: \[d = BC = 10{\rm{ cm}}\].

Suy ra, bán kính đường tròn ngoại tiếp tam giác \[ABC\] là \[R{\rm{ }} = \frac{d}{2}\; = 5{\rm{ }}\left( {{\rm{cm}}} \right)\].

Vậy \[R = 5\,\,{\rm{cm}}.\]

Đáp án đúng là: D

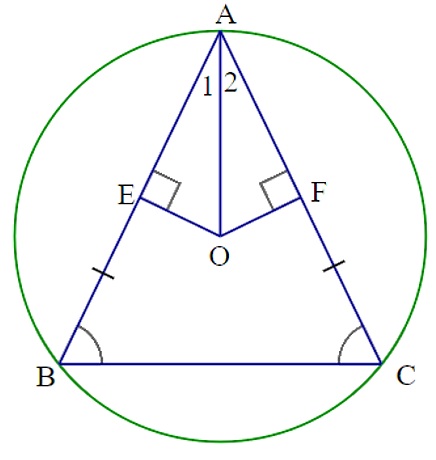
Ta có: \[\Delta ABC\] cân tại \[A\] suy ra \[AB = AC\] do đó \[OE = OF\].

Xét hai tam giác vuông \[AOE\] và \[AOF\] có:

Cạnh \[OA\] chung ; \[OE = OF\] (chứng minh trên)

Suy ra \[\Delta AOE = \Delta AOF\] (cạnh huyền – cạnh góc vuông).

Suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng); \(AE = AF\) (hai cạnh tương ứng).

Vậy \[AO\] là phân giác của \(\widehat {BAC}\).

Đáp án đúng là: A

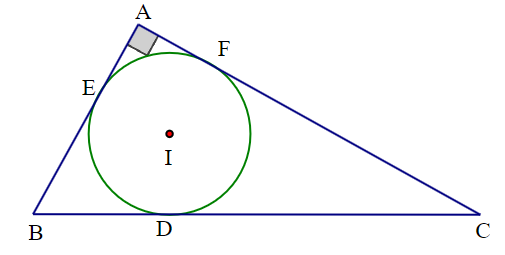
Gọi \[E,{\rm{ }}F\] là tiếp điểm của đường tròn \[\left( I \right)\] với các cạnh \[AB,{\rm{ }}AC\].

Theo tính chất của hai tiếp tuyến cắt nhau, ta có: \[AE = AF;{\rm{ }}BE = BD;\,\,CD = CF\].

Do đó \[2BD = BD + BE\]\[ = BC--CD + AB--AE\]

\[ = BC + AB--\left( {CD + AE} \right)\]\[ = BC + AB--\left( {CF + AF} \right)\]

\[ = BC + AB--AC\].

Suy ra \[BD = \frac{{BC + AB - AC}}{2}\].

Đáp án đúng là: A

Tam giác

\[ABC\] vuông tại \[A\] có đường cao \[AH\] nên \(AB \cdot AC = A{H^2}\).

Mặt khác \(\frac{{AB}}{{AC}} = \frac{3}{4}\) hay \(AB = \frac{3}{4}AC\). Thế vào biểu thức trên ta được:

\(\frac{3}{4}A{C^2} = {\left( {\frac{{12}}{5}} \right)^2}\) hay \(AC = \frac{{8\sqrt 3 }}{5}\,\,\left( {{\rm{cm}}} \right)\).

Suy ra \[AB = \frac{3}{4} \cdot \frac{{8\sqrt 3 }}{5} = \frac{{6\sqrt 3 }}{5}\,\,\left( {{\rm{cm}}} \right)\].

Áp dụng định lý Pythagore vào tam giác \[ABC\] vuông tại \[A\] ta có: \(B{C^2} = A{B^2} + A{C^2}\).

Do đó \(BC = \sqrt {A{B^2} + A{C^2}} = 2\sqrt 3 \,\,\left( {{\rm{cm}}} \right)\).

Tâm đường tròn ngoại tiếp tam giác \[ABC\] là trung điểm O của cạnh huyền \[BC\].

Vậy bán kính đường tròn ngoại tiếp tam giác \[ABC\] là \(R = \frac{{2\sqrt 3 }}{2} = \sqrt 3 \) (cm).