18 câu hỏi trắc nghiệm thuộc Dạng 3: Góc có đỉnh bên trong và bên ngoài đường tròn có đáp án

Câu 1:

Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn . Gọi M, N, P, Q lần lượt là điểm chính giữa các cung AB, BC, CD, DA. Chứng minh rằng : . $M P ⊥ N Q$

Xem đáp án

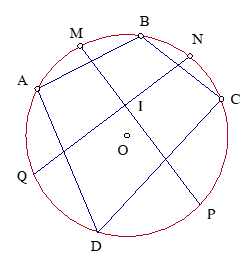
Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn . Gọi M, N, P, Q lần lượt là điểm chính giữa các cung AB, BC, CD, DA. (ảnh 1)

Gọi I là giao điểm của MP và NQ. Ta có.

$\hat{M I Q}$ = $\frac{1}{2}$ (sđ $\overset{⏜}{M Q}$ + sđ $\overset{⏜}{N P}$ )

= $\frac{1}{2}$ . $\frac{1}{2}$ (sđ $\overset{⏜}{A B}$ + sđ $\overset{⏜}{A D}$ + sđ $\overset{⏜}{B C}$ + sđ $\overset{⏜}{C D}$ ).

= $\frac{1}{4} . 360^{o} = 90^{o}$ . Vậy MP ^ NQ.

Câu 2:

Cho đường tròn (O), hai đường kính AB và CD vuông góc với nhau, điểm M thuộc cung nhỏ BC. Gọi E là giao điểm của MA và CD, F là giao điểm của MD và AB. Chứng minh rằng:

a) $\hat{DAE} = \hat{A F D}$

Xem đáp án

a)

Cho đường tròn (O), hai đường kính AB và CD vuông góc với nhau, điểm M thuộc cung nhỏ BC. (ảnh 1)

$\hat{DAE} = \frac{sd \overset{⏜}{DBM}}{2}$ (góc nội tiếp) .

$\hat{AFD} = \frac{sd \overset{⏜}{DB} + s d \overset{⏜}{M B}}{2} = \frac{sd \overset{⏜}{DBM}}{2}$ ( góc có đỉnh ở bên trong đường tròn)

Suy ra $\hat{DAE} = \hat{A F D}$

Câu 3:

b) Khi M di động trên cung nhỏ BC thì diện tích tứ giác AEFD không đổi.

Xem đáp án

b) Ta có: $\hat{D_{1}} = \hat{A_{1}} (= 45^{°})$ và $\hat{E_{1}} = \hat{ADF}$ ( cách chứn minh tương tự câu a) nên $Δ D A E ∽ Δ A D F (g . g)$ Þ $\Rightarrow \frac{D E}{A D} = \frac{A D}{A F} \Rightarrow A F . D E = A D^{2}$ .

Mặt khác AEFD là tứ giác có hai đường chéo AF, DE vuông góc với nhau.

Do đó $S_{A E F D} = \frac{1}{2} AF \cdot DE = \frac{1}{2} {AD}^{2}$ , không đổi.

Câu 4:

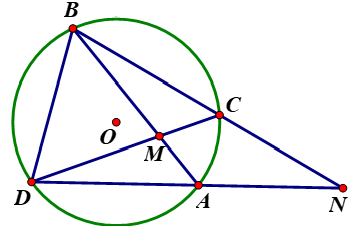
Cho hình vẽ, hãy điền dấu (x) vào ô thích hợp trong bảng sau:

TT	Khẳng định	Đúng	Sai
1	$\hat{A} = \hat{B M D}$
2	$\hat{B M C} = \frac{s đ \overset{⏜}{B C} + s đ \overset{⏜}{A D}}{2}$
3	$\hat{A B N} + \hat{N} = \frac{1}{2} s đ \overset{⏜}{B D}$
4	$\hat{N} = \frac{1}{2} (s đ \overset{⏜}{B D} - s đ \overset{⏜}{A C)}$

Xem đáp án

1. sai 2. đúng 3. đúng 4. đúng

Câu 5:

Cho đường tròn (O) trong đó có ba dây bằng nhau AB, AC, BD sao cho hai dây AC, BD cắt nhau tại M tạo thành góc vuông AMB. Tính số đo các cung nhỏ AB, CD.

Xem đáp án

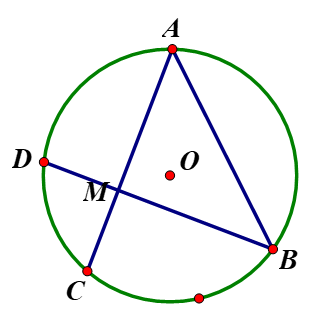
Cho đường tròn (O) trong đó có ba dây bằng nhau AB, AC, BD sao cho hai dây AC, BD cắt nhau tại (ảnh 1)

Đường tròn (O) có dây: AB = AC = BD

Suy ra sđ $\overset{⏜}{A B}$ = sđ $\overset{⏜}{A C}$ = sđ $\overset{⏜}{B D}$

Do đó: sđ $\overset{⏜}{A D}$ = sđ $\overset{⏜}{A C}$ - sđ $\overset{⏜}{C D}$

= sđ $\overset{⏜}{B D}$ - sđ $\overset{⏜}{D C}$ = sđ $\overset{⏜}{B C}$

Theo định lý góc có đỉnh bên trong đường tròn, ta có:

sđ $\overset{⏜}{A D}$ + sđ $\overset{⏜}{B C}$ = 2. sđ $\hat{B M C} = {2.90}^{0} = 180^{0}$

nên sđ

\overset{⏜}{A D}

= sđ

\overset{⏜}{B C}

= 90⁰

Lại có: sđ $\overset{⏜}{A B}$ + sđ $\overset{⏜}{C D}$ = 2. sđ $\hat{A B C} = 180^{0}$

Hơn nữa sđ $\overset{⏜}{A B}$ = sđ $\overset{⏜}{B D}$ = sđ $\overset{⏜}{B C}$ + sđ $\overset{⏜}{D C}$ = 90⁰ + sđ $\overset{⏜}{D C}$

Suy ra: sđ

\overset{⏜}{D C}

= 45⁰; sđ

\overset{⏜}{A B}

= 90⁰ + 45⁰ = 135⁰

Câu 6:

Cho đường tròn (O) và dây AB. Vẽ tiếp tuyến xy // AB có M là tiếp điểm. Chứng minh rằng $∆ A M B$ là tam giác cân.

Xem đáp án

Cho đường tròn (O) và dây AB. Vẽ tiếp tuyến xy // AB có M là tiếp điểm. Chứng minh rằng tam giác AMB là tam giác cân. (ảnh 1)

Ta có $O M ⊥ x y$ (tính chất của tiếp tuyến)

Mà xy // AB nên

Suy ra $\overset{⏜}{M A} = \overset{⏜}{M B}$ (định lý đường kính vuông góc với dây cung)

Do đó MA = MB (hai cung bằng nhau căng hai dây bằng nhau)

Câu 7:

Từ một điểm A ở bên ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC với đường tròn (B và C là các tiếp điểm). Vẽ dây CD // AB. Đường thẳng AD cắt đường tròn tại một điểm thứ hai là E. Tia CE cắt AB tại M. Chứng minh:

a) MB² = MC.ME;

Xem đáp án

a)

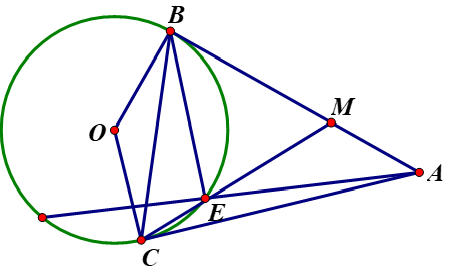
Từ một điểm A ở bên ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC với đường tròn (B và C là các tiếp điểm). Vẽ dây CD // AB. (ảnh 1)

$Δ M B E$ và $Δ M C B$ có

$\hat{M_{1}}$ chung; $\hat{B_{1}} = \hat{C_{2}}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BE)

Nên $Δ M B E$ # $Δ M C B$ (g.g)

Suy ra $\frac{M B}{M C} = \frac{M E}{M B}$

Do đó MB² = MC.ME

Câu 8:

b) M là trung điểm của AB

Xem đáp án

b) Ta có CD // AB nên $\hat{A_{1}} = \hat{D_{1}}$ (cặp góc so le trong)

Mặt khác $\hat{C_{1}} = \hat{D_{1}}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung CE).

ð $\hat{A_{1}} = \hat{C_{1}}$

Xét $Δ M A E$ và $Δ M C A$ có: $\hat{M_{2}}$ chung; $\hat{A_{1}} = \hat{C_{1}}$ (chứng minh trên)

Vậy $Δ M A E$ # $Δ M C A$ (g.g). Suy ra $\frac{M A}{M C} = \frac{M E}{M A}$

Do đó MA² = MC.ME (2)

Từ (1) và (2) suy ra MA² = MB² do đó MA = MB

Câu 9:

Cho hai đường tròn (O) và (O^’) cắt nhau tại A và B. Vẽ dây AC của đường tròn (O) tiếp xúc với đường tròn (O^’). Vẽ dây AD của đường tròn (O^’) tiếp xúc với đường tròn (O). Chứng minh rằng:

a) AB2 = BC.BD

Xem đáp án

a)

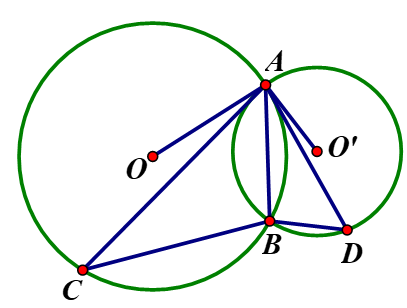
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Vẽ dây AC của đường tròn (O) tiếp xúc với đường tròn (O’). (ảnh 1)

$Δ A B C$ và $Δ D B A$ có

$\hat{A_{1}} = \hat{D_{1}}$ ; $\hat{C} = \hat{A_{2}}$

(góc tạo bởi tia tiếp tuyến và dây cung và

góc nội tiếp cung chắn cung AB)

Do đó $Δ A B C$ # $Δ D B A$ (g.g)

Suy ra

\frac{A B}{B D} = \frac{C B}{A B}

.Vậy AB² = BC.BD

Câu 10:

Chứng minh rằng:

b) $\frac{B C}{B D} = \frac{A C^{2}}{A D^{2}}$

Xem đáp án

b) $Δ A B C$ # $Δ D B A$ (chứng minh trên) => $\frac{A B}{B D} = \frac{C B}{A B} = \frac{A C}{D A}$

Do đó $\frac{A B}{B D} . \frac{C B}{A B} = \frac{A C}{D A} . \frac{A C}{D A}$ . Vậy $\frac{B C}{B D} = \frac{A C^{2}}{A D^{2}}$

Câu 11:

Cho đường tròn (O) và hai đường kính vuông góc AB và CD. Trên cung BD lấy một điểm M. Tiếp tuyến của (O) tại M cắt AB ở E ; CM cắt AB tại F. Chứng tỏ EF = EM.

Xem đáp án

Đường tròn (O) có:

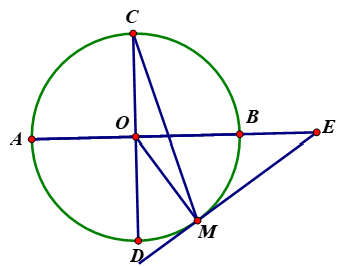
Cho đường tròn (O) và hai đường kính vuông góc AB và CD. Trên cung BD lấy một điểm M. (ảnh 1)

$\hat{E M F} = \frac{1}{2} s đ \overset{⏜}{C B M}$ (góc giữa tiếp tuyến và dây đi qua tiếp điểm)

$\Rightarrow \hat{E M F} = \frac{1}{2} (s đ \overset{⏜}{M B} + s đ \overset{⏜}{B C})$

$\hat{E F M} = \frac{1}{2} (s đ \overset{⏜}{M B} + s đ \overset{⏜}{A C})$ (góc có đỉnh ở trong đường tròn (O)

Mà: $s đ \overset{⏜}{B C} = s đ \overset{⏜}{A C} = 90^{o}$ (vì $C D ⊥ A B$ ).

Do đó:

\hat{E M F} = \hat{E F M} \Rightarrow Δ E F M

cân tại E. Vậy: EF = EM

Câu 12:

Cho tam giác ABC, phân giác trong AD. Đường tròn (O) đi qua A, tiếp xúc với BC tại D. Đường tròn (O) cắt AB, AC tương ứng tại M và N. Chứng minh MN // BC.

Xem đáp án

Chứng minh $Δ B M D$ # $Δ B D A$ , suy ra

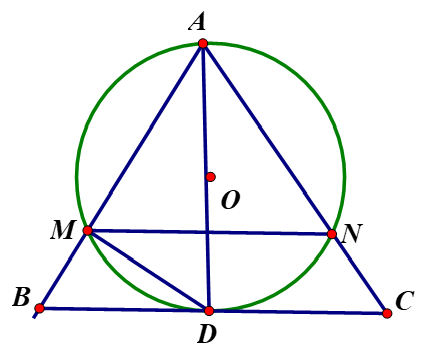
Cho tam giác ABC, phân giác trong AD. Đường tròn (O) đi qua A, tiếp xúc với BC tại D. (ảnh 1)

BD² = BM . BA

Tương tự, cũng có CD² = CN . CA, suy ra

$\frac{B D^{2}}{C D^{2}} = \frac{B M . B A}{C N . C A}$

Mà

\frac{B D}{C D} = \frac{A B}{C A}

, suy ra

\frac{A B^{2}}{C A^{2}} = \frac{B M . B A}{C N . C A}

nên

\frac{B M}{C N} = \frac{B A}{C A} \Rightarrow M N

// BC

Câu 13:

Từ một điểm A ở bên ngoài đường tròn (O), vẽ tiếp tuyến AB và cát tuyến ACD với đường tròn (B là tiếp điểm, C nằm giũa A và D). Tia phân giác của góc CBD cắt đường tròn tại m, cắt CD tại E và cắt tia phân giác của góc BAC tại H. Chứng minh rằng:

a)

A H ⊥ B E

;

Xem đáp án

a)

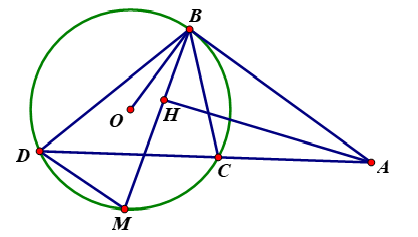
Từ một điểm A ở bên ngoài đường tròn (O), vẽ tiếp tuyến AB và cát tuyến ACD với đường tròn (B là tiếp điểm, C nằm giũa A và D). (ảnh 1)

Vì $\hat{C B M} = \hat{D B M}$ nên $\overset{⏜}{M C} = \overset{⏜}{M D}$

(hai góc nội tiếp bằng nhau thì hai cung bị chắn bằng nhau)

Góc AEB là góc có đỉnh ở bên trong đường tròn nên

$\hat{A E B} = \frac{s đ \overset{⏜}{B C} + s đ \overset{⏜}{M D}}{2}$

= \frac{s đ \overset{⏜}{B C} + s đ \overset{⏜}{M C}}{2} = \frac{s đ \overset{⏜}{B C M}}{2}

(1)

Góc ABM là góc tạo bởi tia tiếp tuyến và dây cung nên sđ $\hat{A B M} = \frac{s đ \overset{⏜}{B C M}}{2}$ (2)

Từ (1) và (2) suy ra $\hat{A E B} = \hat{A B M}$ , do đó $Δ A B E$ cân tại A.

Có AH là tia phân giác của góc A nên $A H ⊥ B E$

Câu 14:

Chứng minh rằng: b) MD² = MB . ME

Xem đáp án

b) $Δ M D E$ và $Δ M B D$ có

$\hat{M D E} = \hat{M B D}$ (hai góc nội tiếp chắn hai cung bằng nhau); $\hat{M}$ chung.

nên $Δ M D E$ # $Δ M B D$ (g. g).

Suy ra $\frac{M D}{M B} = \frac{M E}{M D}$ , do đó MD² = MB. ME

Câu 15:

Cho đường tròn (O) và dây AB. Gọi M là điểm chính giữa của cung nhỏ AB và C là điểm nằm giữa A và B. Tia MC cắt đường tròn tại một điểm thứ hai là D.

a) Chứng minh rằng MA² = MC . MD.

Xem đáp án

a,

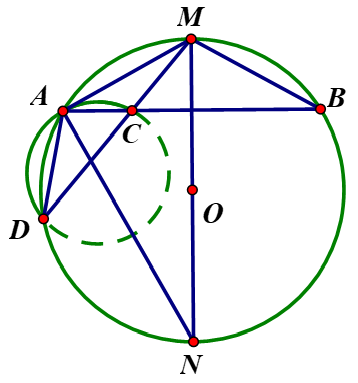
Cho đường tròn (O) và dây AB. Gọi M là điểm chính giữa của cung nhỏ AB và C là điểm nằm giữa A và B. (ảnh 1)

$Δ M A C$ và $Δ M D A$ có: $\hat{M_{1}}$ chung;

$\hat{M A C} = \hat{M D A}$ (hai góc nội tiếp chắn hai cung bằng nhau).

Vậy $Δ M A C$ # $Δ M D A$ (g. g).

Suy ra $\frac{M A}{M D} = \frac{M C}{M A}$ .

Do đó MA² = MC . MD.

Câu 16:

b) Vẽ đường tròn (O’) ngoại tiếp tam giác ACD. Chứng minh rằng AM là tiếp tuyến của đường tròn (O’).

Xem đáp án

b, Ta có: $\hat{M A C} = \hat{D}$ (chứng minh trên), mà $\hat{D} = \frac{s đ \overset{⏜}{A C}}{2}$ , nên $\hat{M A C} = \frac{s đ \overset{⏜}{A C}}{2}$

AM là một tia tiếp tuyến của đường tròn (O’) (Định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung)

Câu 17:

c) Vẽ đường kính MN của đường tròn (O). Chứng minh ba điểm A, O’, N thẳng hàng.

Xem đáp án

c,Ta có $\hat{M A N} = 90^{o}$ (góc nội tiếp chắn nửa đường tròn đường kính MN).

Suy ra $N A ⊥ A M$ . Mặt khác $O' A ⊥ A M$ (tính chất của tiếp tuyến).

Qua điểm A chỉ vẽ được một đường thẳng vuông góc với AM, do đó ba điểm A, O’, N thẳng hàng

Câu 18:

Cho đường tròn (O) và một dây AB. Vẽ đường kính (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm M. Các đường thẳng CM và DM cắt đường thẳng AB lần lượt tại E và F. Tiếp tuyến của đường tròn tại M cắt đường thẳng AB tại N. Chứng minh rằng N là trung điểm của EF.

Xem đáp án

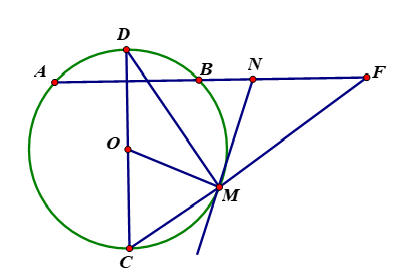
Cho đường tròn (O) và một dây AB. Vẽ đường kính (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm M. (ảnh 1)

Ta sẽ chứng minh NE = NF bằng cách dùng NM làm trung gian.

Ta có $C D ⊥ A B$ nên $\overset{⏜}{D A} = \overset{⏜}{D B}$ và $\overset{⏜}{C A} = \overset{⏜}{C B}$ (định lí đường kính vuông góc với dây cung).

Góc F₁ là góc có đỉnh ở bên trong một đường tròn nên:

${\hat{F}}_{1} = \frac{s đ \overset{⏜}{B M} + s đ \overset{⏜}{A D}}{2} = \frac{s đ \overset{⏜}{B M} + s đ \overset{⏜}{B D}}{2} = \frac{s đ \overset{⏜}{M B D}}{2} (1)$

\hat{M_{3}}

là góc tạo bởi tia tiếp tuyến và dây cung nên

\hat{M_{2}} = \frac{s đ \overset{⏜}{M C}}{2}

(2)

Từ (1) và (2) suy ra $\hat{F_{1}} = \hat{M_{3}}$ do đó $Δ N M F$ cân tại N, suy ra NF = NM.

Góc E là góc có đỉnh ở bên ngoài đường tròn nên: $\hat{E} = \frac{s đ \overset{⏜}{A C} - s đ \overset{⏜}{B M}}{2} = \frac{s đ \overset{⏜}{B C} - s đ \overset{⏜}{B M}}{2} = \frac{s đ \overset{⏜}{M C}}{2}$ (3)

Góc M₂ là góc tạo bởi tia tiếp tuyến và dây cung nên $\hat{M_{2}} = \frac{s đ \overset{⏜}{M C}}{2}$ . (4)

Từ (3) và (4) suy ra $\hat{E} = \hat{M_{2}}$ , dẫn tới $\hat{E} = \hat{M_{1}}$ (vì $\hat{M_{1}} = \hat{M_{2}}$ )

Do đó

Δ N M E

cân, suy ra NE = NM tại N. Do vậy NE = NF. Vậy N là trung điểm của EF