Bài tập Toán 9 Chủ đề 6: Hàm số bậc hai và các bài toán tương giao với đồ thị hàm số bậc nhất có đáp án
Dạng 1. Vị trí tương đối của của đường thẳng và parabol
-
1559 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 5:
 Xem đáp án
Xem đáp án
Thay toạ độ điểm vào công thức hàm số
Ta có ( thỏa mãn)
Vậy điểm thuộc đồ thị hàm số
Câu 6:
 Xem đáp án
Xem đáp án
Thay toạ độ điểm vào công thức xác định hàm số
Ta có ( thỏa mãn)
Vậy điểm thuộc đồ thị hàm số
Câu 7:
 Xem đáp án
Xem đáp án
Thay toạ độ điểm vào công thức hàm số
Ta có ( vô lí)
Vậy điểm không thuộc đồ thị hàm số
Câu 8:
 Xem đáp án
Xem đáp án
Thay toạ độ điểm vào công thức xác định hàm số
Ta có (thỏa mãn)
Vậy điểm thuộc đồ thị hàm số
Câu 9:
Trong hệ toạ độ Oxy, cho hàm số
Tìm m để đồ thị hàm số đi qua các điểm : A(-1;3)
 Xem đáp án
Xem đáp án
Để đồ thị hàm hàm số đi qua điểm
Ta có:
Vậy với m = 1 thì đồ thị hàm số đi qua điểm
Câu 10:
Tìm m để đồ thị hàm số đi qua các điểm :
 Xem đáp án
Xem đáp án
Để đồ thị hàm số đi qua điểm
Ta có:
Vậy với thì đồ thị hàm số đi qua điểm
Câu 11:
 Xem đáp án
Xem đáp án
Thay m = 0 vào công thức hàm số ta có:
- Toạ độ giao điểm của đồ thị hàm số với đồ thị hàm số là nghiệm của hệ phương trình:
- Giải phương trình
Ta có: a + b + c = 2 + (-1) + (-1) = 0 nên phương trình có 2 nghiệm phân biệt ; (hoặc giáo viên cho HS phân tích vế trái thành dạng tích và giải phương trình tích)
+) Với
+) Với
Vậy với m = 0 thì đồ thị hàm số và đồ thị hàm số cắt nhau tại 2 điểm phân biệt và .
Câu 12:
Vẽ đồ thị hàm số (P) và đường thẳng trên cùng một mặt phẳng toạ độ Oxy.
 Xem đáp án
Xem đáp án
Vẽ đồ thị hàm số (P)
Lập bảng giá trị tương ứng giữa x và y.
|
x |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
|
9 |
4 |
1 |
0 |
1 |
4 |
9 |
Đồ thị hàm số (P) là một Parabol có bề lõm quay xuống phía dưới và đi qua các điểm có toạ độ
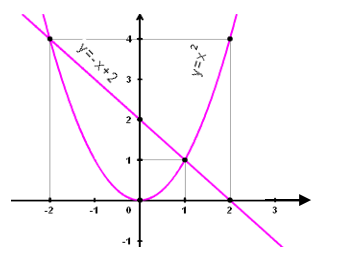
+) Đường thẳng
Cho x = 0 y = 2
y = 0 x = 2
Đường thẳng
đi qua 2 điểm D (0; 2) và E (2; 0)
Câu 13:
Tìm toạ độ giao điểm của (P ) và (d) bằng phép tính.
 Xem đáp án
Xem đáp án
Toạ độ giao điểm của đồ thị hàm số (P) và đường thẳng là nghiệm của hệ phương trình:
- Giải phương trình:
Ta có a + b + c = 1 + 1 + (- 2) = 0 nên phương trình (2) có hai nghiệm ; (hoặc giáo viên cho HS phân tích vế trái thành dạng tích và giải phương trình tích)
+) Với
+) Với
- Vậy đồ thị hàm số (P) và đường thẳng (d) cắt nhau tại 2 điểm và .