Đề kiểm tra 1 tiết Toán 9 Chương 2 Hình học có đáp án (Đề 2)
-
1849 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm
Nội dung câu hỏi 1
Cho đoạn thẳng OI = 8 cm. Vẽ các đường tròn (O; 10cm); (I; 2cm). Hai đường tròn (O) và (I) có vị trí tương đối như thế nào với nhau?
Xem đáp án
Đáp án là C
Câu 2:
Chọn khẳng định sai.
Cho đường tròn (O) đường kính AB. Hai dây AM và BN bằng nhau và nằm khác phía với đường thẳng AB. Khi đó:
Xem đáp án
Đáp án là D
Câu 4:
Cho đường tròn (O;R). Một dây AB của đường tròn có độ dài R . Khoảng cách từ tâm O đến dây AB bằng:
Xem đáp án
Đáp án là B
Câu 6:
Chọn khẳng định đúng.
Cho đường tròn (I) nội tiếp ΔABC. Tâm I của đường tròn này là:
Xem đáp án
Đáp án là A
Câu 7:
Phần tự luận
Nội dung câu hỏi 1
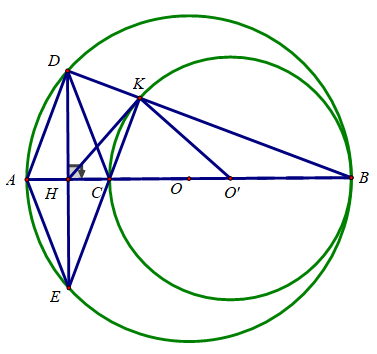
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
a) Hai đường tròn (O) và (O') có vị trí tương đối như thế nào?
Xem đáp án
a) Ta có: OO' = OB – O'B
⇒ Hai đường tròn (O) và (O') tiếp xúc trong tại B
Câu 8:
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì ? Vì sao?
Xem đáp án
b) Dây DE của (O) vuông góc với đường kính AB
⇒ AB đi qua trung điểm của DE hay H là trung điểm của AB
Xét tứ giác ADCE có:
H là trung điểm của AB
H là trung điểm của AC
⇒ Tứ giác ADCE là hình bình hành
Lại có: AC ⊥ DE
⇒ Tứ giác ADCE là hình thoi.
Câu 9:
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
c) Gọi K là giao điểm của DB và đường tròn (O'). Chứng minh rằng 3 điểm E, C, K thẳng hàng.
Xem đáp án
c) Ta có:
∠(CKB) = (Góc nội tiếp chắn nửa đường tròn (O')) ⇒ CK ⊥ BD
∠(ADB) = (Góc nội tiếp chắn nửa đường tròn (O)) ⇒ AD ⊥ BD
⇒ CK // AD
Lại có: CE // AD (Tứ giác ADCE là hình thoi)
⇒ C, E, K thẳng hàng
Câu 10:
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
d) Chứng minh HK là tiếp tuyến của đường tròn (O')
Xem đáp án
d) Xét tam giác DEK vuông tại K có KH là trung tuyến nên KH = HE
ΔKHE có KH = HE ⇒ ΔKHE cân tại H
⇒ ∠(HKE ) = ∠(KEH)
Lại có ΔO'CK cân tại O' ⇒ ∠(O'CK) = (O'KC)
⇒ ∠(HKE ) + ∠(O'KC) = ∠(KEH) + ∠(O'CK)
⇔ ∠(O'KH) = ∠(KEH) + ∠(O'CK)
Mặt khác ∠(O'CK) = ∠(HCE) (đối đỉnh)
ΔHEC vuông tại H nên ∠(KEH) + ∠(HCE) = 90o ⇒ ∠(KEH) + ∠(O'CK) =
Hay ∠(O'KH) =
⇒ KH là tiếp tuyến của (O')