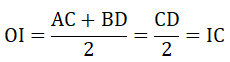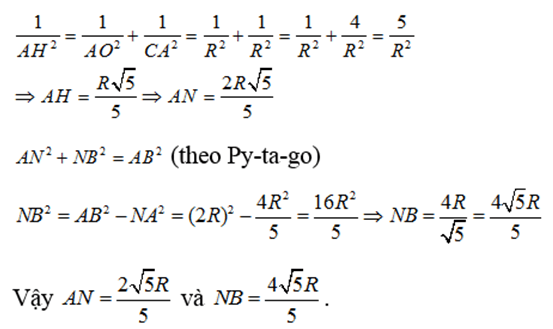Đề kiểm tra 1 tiết Toán 9 Chương 2 Hình học có đáp án (Đề 3)
-
1697 lượt thi
-
11 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm
Nội dung câu hỏi 1
Cho đường thẳng A và điểm O cách a một khoảng là 2 cm. Vẽ đường tròn tâm O, đường kính 4 cm. Khi đó đường thẳng a:
Xem đáp án
Đáp án là B
Câu 2:
Chọn câu khẳng định đúng.
Cho đường tròn (O) hai dây AB và CD cắt nhau tại M nằm trong đường tròn. Gọi E và F lần lượt là trung điểm của AB và CD. Cho biết AB < CD. So sánh MF và ME:
Xem đáp án
Đáp án là A
Câu 3:
Cho hai đường tròn (O;R) và (O’;r) cắt nhau tại hai điểm A và B. Biết OO'=2+2(cm); (AOB) = ; (AO'B) =
Bán kính R, r lần lượt là:
Xem đáp án
Đáp án là C
Câu 6:
Cho tam giác ABC có chu vi bằng 30cm và diện tích bằng 45. Vẽ đường tròn (O) nội tiếp ΔABC. Bán kính của đường tròn đó bằng:
Xem đáp án
Đáp án là D
Câu 7:
Phần tự luận
Nội dung câu hỏi 1
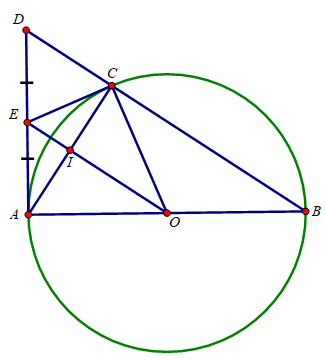
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O). Tiếp tuyến tại A của (O) cắt đường thẳng BC tại D. Gọi E là trung điểm của AD.
a) Chứng minh EC là tiếp tuyến của (O)
Xem đáp án
a) Ta có: ∠(ACB) = (góc nội tiếp chắn nửa đường tròn)
⇒ AC ⊥ BD
ΔACD vuông tại C có CE là trung tuyến nên:
CE = EA = 1/2 AD
Xét ΔAEO và ΔCEO có:
AE = CE
EO : cạnh chung
AO = CO
⇒ ΔAEO = ΔCEO (c.c.c)
⇒ ∠(EAO) = ∠(ECO) =
⇒ CE là tiếp tuyến của (O)
Câu 8:
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O). Tiếp tuyến tại A của (O) cắt đường thẳng BC tại D. Gọi E là trung điểm của AD.
b) Chứng minh EO vuông góc với AC tại trung điểm I của AC.
Xem đáp án
b) EA và EC là 2 tiếp tuyến của (O) cắt nhau tại E
⇒ EA = EC
Lại có: OA = OC
⇒ OE là đường trung trực của đoạn AC hay OE vuông góc với AC tại trung điểm I của AC
Câu 9:
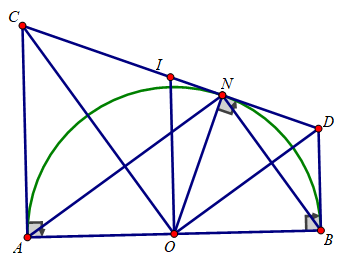
Cho nửa đường tròn (O) đường kính AB = 2R, N là điểm trên nửa đường tròn. Trên cùng một nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và một tiếp tuyến tại N cắt hai tiếp tuyến Ax và By lần lượt tại C và D.
a) Chứng minh AC + BD = CD và AC.BD không đổi.
Xem đáp án
a)Ta có: DN và DB là hai tiếp tuyến cắt nhau tại D ⇒ DN = DB
CA và CN là hai tiếp tuyến cắt nhau tại C ⇒ CA = CN
Khi đó: DB + CA = DN + CN = DC
Mặt khác OC và OD lần lượt là hai phân giác của hai góc ∠(AON) và ∠(BON) kề bù nên
∠(COD) =
Trong tam giác vuông COD có ON là đường cao nên:
DN.CN = =
Hay AC.BD = (không đổi)
Câu 10:
Cho nửa đường tròn (O) đường kính AB = 2R, N là điểm trên nửa đường tròn. Trên cùng một nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và một tiếp tuyến tại N cắt hai tiếp tuyến Ax và By lần lượt tại C và D.
b) Chứng minh AB tiếp xúc với đường tròn đường kính CD.
Xem đáp án
b) Gọi I là tâm của đường tròn đường kính CD.
Tứ giác CABD là hình thang vuông (AC ⊥ AB;BD ⊥ AB) có OI là đường trung bình
⇒ OI // AC ; mà AC ⊥ AB ⇒ OI ⊥ AB tại O
Vậy AB tiếp xúc với đường tròn đường kính CD.
Câu 11:
Cho nửa đường tròn (O) đường kính AB = 2R, N là điểm trên nửa đường tròn. Trên cùng một nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và một tiếp tuyến tại N cắt hai tiếp tuyến Ax và By lần lượt tại C và D.
c) Biết AC = R/2. Tính NA và NB.
Xem đáp án
c)Ta có: OA = ON (bằng R)
CA = CN (tính chất hai tiếp tuyến cắt nhau)
Do đó OC là đường trung trực của AN. Gọi H là giao điểm của OC và AN. Xét tam giác vuông CAO có AH là đường cao nên:
