Đề thi giữa kì 1 môn Toán lớp 9 Cánh diều có đáp án (Đề 1)
-
328 lượt thi
-
10 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Điều kiện xác định của phương trình \(\frac{1}{{x\left( {{x^2} + 4} \right)}} = \frac{{x + 1}}{x} - \frac{1}{{x - 2}}\) là \[x \ne 0\] và \[x - 2 \ne 0,\] hay \[x \ne 0\] và \[x \ne 2\].
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phương trình bậc nhất hai ẩn có dạng \(ax + by = c\) với \(a \ne 0\) hoặc \(b \ne 0.\)
Phương trình \(\frac{1}{x} + 2y = - 3\) không có dạng trên, có chứa ẩn \(x\) dưới mẫu thức nên đây không phải phương trình bậc nhất hai ẩn.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Cách 1. Sử dụng MTCT để tìm nghiệm của hệ hai phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)
Với MTCT phù hợp, ta bấm lần lượt các phím:
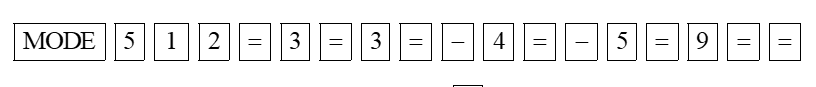
Trên màn hình cho kết quả \(x = - 21,\) ta bấm tiếp phím màn hình cho kết quả \(y = 15.\)
Vậy cặp số \(\left( { - 21;\,\,15} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)
Cách 2. Thay \(x = 1;\,\,y = 1\) vào hệ phương trình đã cho, ta được: \(\left\{ \begin{array}{l}2 \cdot 1 + 3 \cdot 1 = 5\,\,\left( { \ne 3} \right)\\ - 4 \cdot 1 - 5 \cdot 1 = - 9\,\,\left( { \ne 9} \right)\end{array} \right..\)
Tương tự, thay giá trị của \(x\) và \(y\) lần lượt của các cặp số ở phương án B, C, D vào hệ phương trình đã cho, ta thấy chỉ có cặp số \(\left( { - 21;\,\,15} \right)\) là nghiệm của cả hai phương trình trong hệ.
Vậy cặp số \(\left( { - 21;\,\,15} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)
Cách 3. Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)
Nhân hai vế của phương trình thứ nhất với \(2,\) ta được hệ phương trình mới \(\left\{ \begin{array}{l}4x + 6y = 6\\ - 4x - 5y = 9.\end{array} \right.\)
Cộng từng vế hai phương trình của hệ phương trình trên, ta được: \(y = 15.\)
Thay \(y = 15\) vào phương trình \(2x + 3y = 3,\) ta được:
\(2x + 3 \cdot 15 = 3,\) hay \(2x + 45 = 3,\) suy ra \(2x = - 42,\) nên \(x = - 21.\)
Vậy hệ phương trình đã cho có nghiệm duy nhất là \(\left( { - 21;\,\,15} \right).\)
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
⦁ Do \(5 > 3\) nên \(5a > 3a\) khi \(a > 0\) và \(5a < 3a\) khi \(a < 0\). Do đó phương án A và B là sai.
⦁ \(5 > 3\) nên \(5 + a > 3 + a.\) Do đó phương án C là đúng.
⦁ Do \( - 3 > - 6\) nên \( - 3a > - 6a\) khi \(a > 0\). Do đó phương án D là sai.
Vậy ta chọn phương án C.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bất phương trình bậc nhất một ẩn là bất phương trình \(2y \ge 10 - y\).
Bất phương trình \(3 - \frac{2}{y} < 0\) có chứa ẩn \(y\) dưới mẫu, bất phương trình \(\frac{1}{2}x - y \le 3\) có hai ẩn \(x\) và \(y\), bất phương trình \(1 + 0y > 5\) có hệ số \(a = 0\) nên những bất phương trình này không phải bất phương trình bậc nhất một ẩn.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
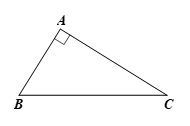
Tam giác \[ABC\] vuông tại \[A\], ta có: \[\sin \widehat {ABC} = \frac{{AC}}{{BC}}\].
Vậy ta chọn phương án A.Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Với \(\alpha + \beta = 90^o ,\) ta có: \(\sin \alpha = \cos \beta ;\,\,\cos \alpha = \sin \beta ;\,\,\tan \alpha = \cot \beta ;\,\,\cot \alpha = \tan \beta .\)
Vậy ta chọn phương án B.
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
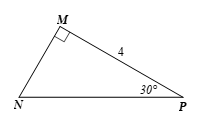
Tam giác \(MNP\) vuông tại \(M\), ta có:
⦁ góc \(P\) là góc nhọn nên \(\tan P \cdot \cot P = 1\);
⦁ \(\widehat {N\,} = 90^o - \widehat {P\,} = 90^o - 30^o = 60^\circ \);
⦁ \(MN = MP \cdot \tan P = 4 \cdot \tan 30^o = \frac{{4\sqrt 3 }}{3}\);
⦁ \(MP = NP \cdot \cos P,\) suy ra \(NP = \frac{{MP}}{{\cos P}} = \frac{4}{{\cos 30^o }} = \frac{4}{{\frac{{\sqrt 3 }}{2}}} = \frac{{8\sqrt 3 }}{3}.\)
Vậy phương án B là nhận định sai, ta chọn phương án B.
Câu 9:
1. Xác định hàm số \(y = ax + b\) để đồ thị của nó đi qua hai điểm \(A\left( {1;\,\, - 1} \right)\) và \(B\left( {4;\,\,5} \right)\).
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một ôtô dự định đi từ A đến B trong khoảng thời gian nhất định. Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi chậm mất so với dự định là 5 giờ. Tính vận tốc và thời gian dự định của ôtô.
 Xem đáp án
Xem đáp án
1. Vì đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A\left( {1;\,\, - 1} \right)\) và \(B\left( {4;\,\,5} \right)\) nên thay lần lượt từng cặp giá trị \(x,\,\,y\) vào hàm số, ta có: \(\left\{ \begin{array}{l} - 1 = a \cdot 1 + b\\5 = a \cdot 4 + b\end{array} \right.\) hay \(\left\{ \begin{array}{l}a + b = - 1\\4a + b = 5.\end{array} \right.\)
Trừ từng vế phương trình thứ hai cho phương trình thứ nhất của hệ phương trình trên, ta được:
\(3a = 6,\) suy ra \(a = 2.\)
Thay \(a = 2\) vào phương trình \(a + b = - 1,\) ta được:
\(2 + b = - 1,\) suy ra \(b = - 3.\)
Vậy hàm số cần tìm là \(y = 2x - 3.\)
2. Gọi \(x\) (km/h) là vận tốc dự định của ôtô và \(y\) (giờ) là thời gian dự định của ôtô để đi hết quãng đường AB \(\left( {x > 10,\,\,y > 0} \right).\)
– Quãng đường AB là \(xy\) (km).
– Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Khi đó, ta có:
⦁ Vận tốc của ôtô lúc này là: \(x + 10\) (km/h).
⦁ Thời gian ôtô đi hết quãng đường AB là: \(y - 3\) (giờ).
⦁ Quãng đường AB là: \(\left( {x + 10} \right)\left( {y - 3} \right)\) (giờ).
Ta có phương trình: \(\left( {x + 10} \right)\left( {y - 3} \right) = xy\)
\(xy - 3x + 10y - 30 = xy\)
\( - 3x + 10y = 30\) (1)
– Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi muộn hơn so với dự định là 5 giờ. Khi đó, ta có:
⦁ Vận tốc của ôtô lúc này là: \(x - 10\) (km/h).
⦁ Thời gian ôtô đi hết quãng đường AB là: \(y + 5\) (giờ).
⦁ Quãng đường AB là: \(\left( {x + 10} \right)\left( {y + 5} \right)\) (giờ).
Ta có phương trình: \[\left( {x - 10} \right)\left( {y + 5} \right) = xy\]
\(xy + 5x - 10y - 50 = xy\)
\(5x - 10y = 50\) (2)
Từ phương trình (1) và phương trình (2) ta có hệ phương trình: \(\left\{ \begin{array}{l} - 3x + 10y = 30\\5x - 10y = 50\end{array} \right.\)
Cộng từng vế hai phương trình của hệ, ta được: \(2x = 80,\) suy ra \[x = 40\] (thỏa mãn).
Thay \[x = 40\] vào phương trình (1), ta được:
\( - 3 \cdot 40 + 10y = 30\) hay \(10y = 150,\) suy ra \(y = 15\) (thỏa mãn).
Vậy vận tốc dự định của ôtô là 40 (km/h) và thời gian ôtô đi hết quãng đường AB là 15 (giờ).
Câu 10:
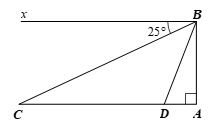
a) Tính chiều cao của đài quan sát (làm tròn kết quả đến hàng đơn vị của mét), biết độ cao từ tầm mắt của người đó đến đỉnh đài quan sát là \[3\] m.
b) Tính số đo góc \[\alpha \] (làm tròn kết quả đến hàng đơn vị của phút).
c) Tính khoảng cách từ mắt người quan sát đến vị trí \[D\] (làm tròn kết quả đến hàng đơn vị của mét).
 Xem đáp án
Xem đáp án
Đổi \(1,221{\rm{\;km}} = 1\,\,221{\rm{\;m}}.\)
a) Do \[Bx\,{\rm{//}}\,AC\;\] nên \[\widehat {ACB} = \widehat {CBx}\] (so le trong).
Vì \(\Delta ABC\) vuông tại \[A\] nên \(AB = AC \cdot {\rm{tan}}\widehat {ACB} = 1\,\,221 \cdot {\rm{tan}}25^\circ \approx 569{\rm{\;(m)}}{\rm{.}}\)
Vậy chiều cao của đài quan sát khoảng: \[3 + 569 = 572\] (m).
b) Đổi: \[60\] km/h \[ = 1{\rm{ }}000\] m/phút.
Do \[Bx\,{\rm{//}}\,AC\;\] và \[AB \bot AC\] nên ta có \(\widehat {ABx} = \widehat {BAC} = 90^\circ .\)
Quãng đường \[CD\] là: \[CD = 1{\rm{ }}000 \cdot 1 = 1{\rm{ }}000\] (m).
Do đó: \[AD = AC - CD = 1{\rm{ }}221\; - 1{\rm{ }}000 = 221\] (m).
Xét \(\Delta ABD\) vuông tại \[A\] có: \({\rm{tan}}\widehat {ABD} = \frac{{AD}}{{AB}} \approx \frac{{221}}{{569}}.\) Suy ra \(\widehat {ABD} \approx 21^\circ 14'.\)
Mà \(\widehat {DBx} + \widehat {ABD} = \widehat {ABx} = 90^\circ .\)
Suy ra \(\alpha = \widehat {DBx} = 90^\circ - \widehat {ABD} \approx 90^\circ - 21^\circ 14' = 68^\circ 46'.\)
c) Vì \(\Delta ABD\) vuông tại \[A\] nên \(AB = BD \cdot {\rm{cos}}\widehat {ABD}.\)
Suy ra \(BD = \frac{{AB}}{{{\rm{cos}}\widehat {ABD}}} \approx \frac{{569}}{{{\rm{cos}}\,21^\circ 14'}} \approx 610{\rm{\;(m)}}{\rm{.}}\)
Vậy khoảng cách từ mắt người quan sát đến vị trí \[D\] khoảng \[610\] mét.
