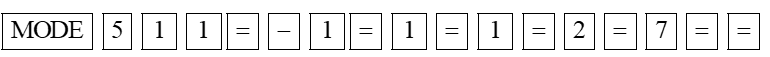Đề thi giữa kì 1 môn Toán lớp 9 Cánh diều có đáp án (Đề 2)
-
223 lượt thi
-
8 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Đáp án đúng là: B
Điều kiện xác định của phương trình \(\frac{1}{{x - 3}} - 3 = \frac{2}{{\left( {x - 3} \right)\left( {x + 4} \right)}}\) là \[x - 3 \ne 0\] và \[x + 4 \ne 0,\] hay \[x \ne 3\] và \[x \ne - 4\].
Câu 2:
Xem đáp án
Đáp án đúng là: A
Ta có: \(a < b\) và \(ac > bc\) nên ta có \(c < 0\), tức \(c\) là số âm.
Vậy ta chọn phương án A.
Câu 3:
Xem đáp án
Đáp án đúng là: B
Cách 1. Sử dụng MTCT để tìm nghiệm của hệ hai phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + 2y = 7.\end{array} \right.\)
Với MTCT phù hợp, ta bấm lần lượt các phím:
Trên màn hình cho kết quả \(x = 3,\) ta bấm tiếp phím = màn hình cho kết quả \(y = 2.\)
Vậy cặp số \(\left( {3;\,\,2} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + 2y = 7.\end{array} \right.\)
Cách 2. Thay \(x = 2,\,\,y = 3\) vào hệ phương trình đã cho, ta được: \(\left\{ \begin{array}{l}2 - 3 = - 1 \ne 1\\2 + 2 \cdot 3 = 8 \ne 7\end{array} \right..\)
Tương tự, thay giá trị của \(x\) và \(y\) lần lượt của các cặp số ở phương án B, C, D vào hệ phương trình đã cho, ta thấy chỉ có cặp số \(\left( {3;\,\,2} \right)\) là nghiệm của cả hai phương trình trong hệ.
Vậy cặp số \(\left( {3;\,\,2} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + 2y = 7.\end{array} \right.\)
Cách 3. Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + 2y = 7.\end{array} \right.\)
Trừ từng vế phương trình thứ hai cho phương trình thứ nhất của hệ phương trình trên, ta được:
\(3y = 6\) nên \(y = 2.\)
Thay \(y = 2\) vào phương trình \(x - y = 1,\) ta được:
\(x - 2 = 1,\) suy ra \(x = 3.\)
Vậy hệ phương trình đã cho có nghiệm duy nhất là \(\left( {3;\,\,2} \right)\).
Câu 4:
Xem đáp án
Đáp án đúng là: D
Vận tốc tối đa mà xe máy đi trên quãng đường đó là \(40\) km/h nên ta có \(a \le 40\).
Câu 5:
Xem đáp án
Đáp án đúng là: C
Ta có: \( - x - 1 > 5\)
\( - 5 - 1 > x\)
\(x < - 5 - 1\).
Vậy ta chọn phương án C.
Câu 6:
Xem đáp án
Đáp án đúng là: A
![Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha .\) Tỉ số \(\frac{{HA}}{{BA}}\) bằng: A. \(\sin \alpha \). B. \[\cos \alpha \]. C. \(\tan \alpha \). D. \(\cot \alpha \). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid1-1727876680.png)
Xét \(\Delta ABH\) vuông tại \[H,\] ta có \(\frac{{AH}}{{AB}} = \sin B\) hay \(\frac{{HA}}{{BA}} = \sin \alpha \).
Vậy ta chọn phương án A.Câu 7:
Xem đáp án
Đáp án đúng là: B
Ta có \(\cot \left( {90^\circ - \alpha } \right) = \tan \alpha = \frac{4}{3}.\)
