Chuyên đề 3: Giải bài toán bằng cách lập phương trình có đáp án
-
1609 lượt thi
-
36 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Tình cảm gia đình có sức mạnh phi trường. Bạn Vì Quyết Chiến - Cậu bé 13 tuổi qua thương nhớ em trai của mình đã vượt qua một quãng đường dài 180km từ Sơn La đến bệnh viện Nhi Trung ương Hà Nội để thăm em. Sau khi đi bằng xe đạp 7 giờ, bạn ấy được lên xe khách và đi tiếp 1 giờ 30 phút nữa thì đến nơi. Biết vận tốc của xe khách lớn hơn vận tốc của xe đạp là 35km/h. Tính vận tốc xe đạp của bạn Chiến.
 Xem đáp án
Xem đáp án
Đổi 1 giờ 30 phút = 1,5 giờ.
Gọi vận tốc xe đạp của bạn Chiến là x (km/h, x > 0)
Vận tốc của ô tô là x + 35 (km/h)
Quãng đường bạn Chiến đi bằng xe đạp là: 7x (km)
Quãng đường bạn Chiến đi bằng ô tô là: 1,5(x + 35) (km)
Do tổng quãng đường bạn Chiến đi là 180km nên ta có phương trình:
(thỏa mãn)
Vậy bạn Chiến đi bằng xe đạp với vận tốc là 15 km/h.
Câu 2:
Bác Bình gửi tiết kiệm 100 triệu đồng vào ngân hàng A, kì hạn một năm. Cùng ngày, bác gửi tiết kiệm 150 triệu đồng vào ngân hàng B, kì hạn một năm, với lãi suất cao hơn lãi suất của ngân hàng A là 1% / năm. Biết sau đúng 1 năm kể từ ngày gửi tiền. Bác Bình nhận được tổng sổ tiền lãi là 16,5 triệu đồng từ hai khoản tiền gửi tiết kiệm nêu trên. Hỏi lãi suất tiền gửi tiết kiệm kì hạn một năm của ngân hàng A là bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Gọi lãi suất gửi tiết kiệm kì hạn một năm của ngân hàng A là x%/ năm. (x > 0)
Thì lãi suất gửi tiết kiệm kì hạn một năm của ngân hàng B là (x + 1)%/ năm.
Tiền lãi bác Bình nhận được sau 1 năm gửi vào ngân hàng A là : 100x% (triệu đồng)
Tiền lãi bác Bình nhận được sau 1 năm gửi vào ngân hàng B là : 150(x + 1)% (triệu đồng)
Tổng số tiền lãi bác Bình nhận được từ hai khoản tiết kiệm trên là 16,5 triệu đồng nên ta có phương trình :
(thỏa mãn )
Vậy lãi suất tiền gửi tiết kiệm kì hạn một năm của ngân hàng A là 6%
Câu 3:
Trên một khúc sông với 2 bờ song song với nhau, có một chiếc đò dự định chèo qua sông từ vị trí A ở bở bên này sang vị trí B ở bờ bên kia, đường thẳng AB vuông góc với các bờ sông. Do bị dòng nước đẩy xiên nên chiếc đò đã cập bờ bên kia tại vị trí C cách B mội khoảng bằng 30 m. Biết khúc sông rộng 150 m, hỏi dòng nước đã đẩy chiếc đò lệch đi một góc có số đo bằng bao nhiêu? (kết quả làm tròn đến giây).
 Xem đáp án
Xem đáp án
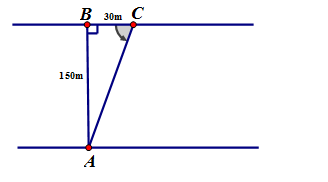
Ta có hình vẽ :
Ta có vuông tại B
Do đó
Vậy dòng nước đã đẩy chiếc đò đi lệch một góc có số đo bằng
Câu 4:
Một đội công nhân đặt kế hoạch sản xuất 250 sản phẩm. Trong 4 ngày đầu, họ thực hiện đúng kế hoạch. Mỗi ngày sau đó, họ đều vượt mức 5 sản phẩm nên đã hoàn thành công việc sớm hơn 1 ngày so với dự định. Hỏi theo kế hoạch, mỗi ngày đội công nhân đó làm được bao nhiêu sản phẩm? Biết rằng năng suất làm việc của mỗi công nhân là như nhau.
 Xem đáp án
Xem đáp án
Gọi số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là x(sp).ĐK
Khi đó, số sản phẩm mỗi ngày đội công nhân đó làm trong thực tế là x + 5 (sp)
Thời gian hoàn thành công việc theo kế hoạch là (ngày)
Số sản phẩm làm được trong 4 ngày đầu là: 4x (sp)
Số sản phẩm còn lại phải làm là 250 - 4x (sp)
Thời gian làm 250 - 4x (sp) còn lại là (ngày).
Theo bài toán ta có PT:
Giải PT này ta được: (nhận)
(loại)
Vậy số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là 25 sản phẩm.
Câu 5:
Hai người thợ cùng làm một công việc trong 9 ngày thì xong. Mỗi ngày, lượng công việc của người thợ thứ hai làm được nhiều gấp ba lần lượng công việc của người thợ thứ nhất. Hỏi nếu làm một mình thì mỗi người làm xong công việc đó trong bao nhiêu ngày
 Xem đáp án
Xem đáp án
Gọi x (ngày), y (ngày) lần lượt là thời gian hoàn thành công việc một mình của người thứ nhất và người thứ hai,
Do hai người cùng làm trong 9 ngày thì xong công việc nên: (1)
Trong cùng một ngày người thứ hai làm được nhiều gấp ba lần người thứ nhất nên (2)
Từ (1) và (2) giải hệ tìm được x = 36; y = 12 (thỏa mãn).
Vậy nếu làm một mình xong công việc người thứ nhất làm hết 36 ngày, người thứ hai làm hết 12 ngày.
Câu 6:
Trong kỳ thi tuyển sinh vào lớp 10 năm học 2019 – 2020, số thí sinh vào trường THPT chuyên bằng số thí sinh thi vào trường PTDT Nội trú. Biết rằng tổng số phòng thi của cả hai trường là 80 phòng thi và mỗi phòng thi có đúng 24 thí sinh. Hỏi số thí sinh vào mỗi trường bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi số thí sinh vào trường THPT Chuyên và số thí sinh vào trường PTDT Nội trú lần lượt là x , y (thí sinh) (điều kiện x > 0, y > 0)
Vì số thí sinh vào trường THPT Chuyên bằng số thí sinh vào trường PTDT Nội trú nên ta có: (1)
Vì tổng số phòng thi của cả hai trường là 80 phòng thi và mỗi phòng thi có đúng 24 thí sinh nên tổng số thí sinh của cả hai trường là:
24.80 = 1920 (thí sinh)
Do đó ta có phương trình; x + y = 1920 (2)
Từ (1) và (2) ta có hệ phương trình
Đối chiếu điều kiện ta thấy x = 768; y = 1152 đều thỏa mãn.
Vậy số thí sinh vào trường THPT Chuyên và số thí sinh vào trường PTDT Nội trú lần lượt là 768 thí sinh , 1152 thí sinh.
Câu 7:
Hưởng ứng Ngày Chủ nhật xanh do UBND tỉnh phát động với chủ đề “Hãy hành động để Thừa Thiên Huế thêm Xanh, Sạch, Sáng”, một trường THCS đã cử học sinh của hai lớp 9A và 9B cùng tham gia làm tổng vệ sinh một con đường, sau giờ thì làm xong công việc. Nếu làm riêng từng lớp thì thời gian học sinh lớp 9A làm xong công việc ít hơn thời gian học sinh lớp 9B là 2 giờ. Hỏi nếu mỗi lớp làm riêng thì sau bao nhiêu giờ sẽ làm xong công việc?
 Xem đáp án
Xem đáp án
Gọi thời gian lớp 9A làm một mình xong công việc là x (giờ)
Gọi thời gian lớp 9B làm một mình xong công việc là y (giờ) (y > 2)
Mỗi giờ lớp 9A làm được phần công việc là: (công việc)
Mỗi giờ lớp 9B làm được phần công việc là: (công việc)
Mỗi giờ lớp cả hai ớp 9A, 9B làm được phần công việc là: (công việc)
Theo đề bài, hai lớp cùng làm chung công việc trong giờ thì xong công việc nên ta có phương trình:
(1)
Nếu làm riêng từng lớp thì thời gian học sinh lớp 9A làm xong công việc ít hơn thời gian lớp 9B là 2 giờ nên ta có phương trình:
y = x + 2 (2)
Thế phương trình (2) vào phương trình (1) ta được:
Vậy nếu làm một mình thì lớp 9A làm xong công việc trong 5 giờ, lớp 9B làm xong công việc trong 5 + 2 = 7 giờ
Câu 8:
Quy tắc sau đây cho ta biết được ngày thứ n, tháng t, năm 2019 là ngày thứ mấy trong tuần. Đầu tiên, ta tính giá trị của biểu thức T = n + H, ở đây H được xác định bởi bảng sau:

Sau đó, lấy T chia cho 7 ta được số dư r .
Nếu r = 0 thì ngày đó là ngày thứ Bảy.
Nếu r = 1 thì ngày đó là ngày Chủ Nhật.
Nếu r = 2 thì ngày đó là ngày thứ Hai.
Nếu r = 3 thì ngày đó là ngày thứ Ba.
…
Nếu r = 6 thì ngày đó là ngày thứ Sáu.
Ví dụ:
Ngày có . Số 31 chia cho 7 có số dư là 3 nên ngày đó là thứ Ba.
a. Em hãy sử dụng quy tắc trên để xác định các ngày và là ngày thứ mấy?
b. Bạn Hằng tổ chức sinh nhật của mình trong tháng 10/2019. Hỏi ngày sinh nhật của Hằng là ngày mấy? Biết rằng ngày sinh nhật của Hằng là một bội số của 3 và là thứ Hai.
 Xem đáp án
Xem đáp án
a. Ngày , có n = 2, t = 9, H = 0. Do đó .
Số 2 chia cho 7 có số dư là 2 nên ngày này là thứ Hai.
Ngày có . Do đó .
Số 18 chia cho 7 có số dư là 4 nên ngày này là thứ Tư.
b. Do ngày sinh nhật của Hằng là vào thứ Hai nên r = 2. Do đó .
Mặt khác .
Biện luận

Do n là bội của 3 nên chọn n = 21.
Vậy sinh nhật của ngày vào ngày .
Câu 9:
Một nhóm gồm 31 học sinh tổ chức một chuyến du lịch (chi phí chuyến đi được chia đều cho các bạn tham gia). Sau khi đã hợp đồng xong, vào giờ chót có 3 bạn bận việc đột xuất không đi được nên họ không đóng tiền. Cả nhóm thống nhất mỗi bạn còn lại sẽ đóng thêm 18000 đồng so với dự kiến ban đầu để bù lại cho 3 bạn không tham gia. Hỏi tổng chi phí mỗi chuyến đi là bao nhiêu?
 Xem đáp án
Xem đáp án
Số tiền cả lớp phải đóng bù: ngàn
Số tiền mỗi học sinh phải đóng: ngàn
Tổng chi phí ban đầu là: ngàn
Câu 10:
Bạn Dũng trung bình tiêu thụ 15 ca-lo cho mỗi phút bơi và 10 ca-lo cho mỗi phút chạy bộ. Hôm nay, Dũng mất 1,5 giờ cho cả hai hoạt động trên và tiêu thụ hết 1200 ca-lo. Hỏi hôm nay, bạn Dũng đã mất bao nhiêu thời gian cho mỗi hoạt động này?
 Xem đáp án
Xem đáp án
Đổi: 1,5 giờ = 90 phút.
Gọi x (phút) là thơi gian Dũng bơi
y (phút) là thời gian Dũng chạy bộ
Theo giải thiết ta có hệ phương trình :
![]()
Vậy Dũng mất 60 phút để bơi và 30 phút để chạy bộ để tiêu thụ hết 1200 ca-lo.
Câu 11:
Một mảnh vườn hình chữ nhật có diện tích . Biết rằng, chiều dài mảnh vườn hơn chiều rộng mảnh vườn là 5m. Tính chiều rộng mảnh vườn.
 Xem đáp án
Xem đáp án
Gọi x, y lần lượt là chiều dài, chiều rộng của mảnh vườn, điều kiện x > 0, y > 0, x > y.
Có
.
Vậy chiều rộng mảnh vườn là 10 (m)
Câu 12:
Lớp 9A và lớp 9B của một trường THCS dự định làm 90 chiếc đèn ông sao để tặng các em thiếu nhi nhân dịp Tết Trung Thu. Nếu lớp 9A làm trong 2 ngày và lớp 9B làm trong 1 ngày thì được 23 chiếc đèn; nếu lớp 9A làm trong 1 ngày và lớp 9B làm trong 2 ngày thì được 22 chiếc đèn. Biết rằng số đèn từng lớp làm được trong mỗi ngày là như nhau, hỏi nếu cả hai lớp cùng làm thì hết bao nhiêu ngày để hoàn thành công việc đã dự định ?
 Xem đáp án
Xem đáp án
Gọi số đèn mà lớp 9A, lớp 9B làm được trong 1 ngày lần lượt là .
Theo bài ra ta có hệ phương trình
Giải hệ phương trình trên ta thu được .
Suy ra trong một ngày cả 2 lớp làm được 8 + 7 = 15 chiếc đèn.
Vậy nếu cả 2 lớp cùng làm thì hết ngày sẽ xong công việc đã dự định.
Câu 13:
Hai ô tô khởi hành cùng một lúc từ A đến B. Vận tốc của ô tô thứ nhất lớn hơn vận tốc của ô tô thứ hai là 10 km/h nên ô tô thứ nhất đến B trước ô tô thứ hai giờ. Tính vận tốc mỗi ô tô biết quãng đường AB dài 150 km.
 Xem đáp án
Xem đáp án
Gọi x (km/h) là vận tốc ô tô thứ nhất. Điều kiện x > 10
Khi đó vận tốc ô tô thứ hai là x - 10 (km/h)
Từ giả thiết ta có
Do x > 10 nên nhận x = 60.
Vậy vận tốc của ô tô thứ nhất là 60 km/h và vận tốc của ô tô thứ hai là 50 km/h.
Câu 14:
An đếm số bài kiểm tra một tiết đạt điểm 9 và điểm 10 của mình thấynhiều hơn 16 bài. Tổng số điểm của tất cả các bài kiểm tra đạt điểm 9 và điểm 10 đó là 160. Hỏi An được bao nhiêu bài điểm 9 và bao nhiêu bài điểm 10?
 Xem đáp án
Xem đáp án
Gọi số bài điểm 9 và điểm 10 của An đạt được lần lượt là x, y (bài) .
Theo giả thiết x + y > 16.
Vì tổng số điểm của tất cả các bài kiểm tra đó là 160 nên 9x + 10y = 160.
Ta có .
Do và nên x + y = 17.
Ta có hệ (thỏa mãn).
Vậy An được 10 bài điểm 9 và 7 bài điểm 10.
Câu 15:
Một công ty vận tải dự định dùng loại xe lớn để vận chuyển 20 tấn hàng hóa theo một hợp đồng. Nhưng khi vào việc, công ty không còn xe lớn nên phải thay bằng những xe nhỏ. Mỗi xe nhỏ vận chuyển được khối lượng ít hơn 1 lần so với mỗi xe lên theo dự định. Để đảm bảo thời gian đã hợp đồng, công ty phải dùng một số lượng xe nhiều hơn số xe dự định là 1 xe. Hỏi mỗi xe nhỏ vận chuyển bao nhiêu tấn hàng hóa? (Biết các xe cùng loại thi có khối lượng vận chuyển như nhau).
 Xem đáp án
Xem đáp án
Gọi số tấn hàng hóa mỗi xe nhỏ vận chuyển được là: x (tấn) (x > 0)
Mỗi xe lớn vận chuyển được số tấn hàng là: x + (tấn)
Khi đó số xe nhỏ dự định phải dùng để chở hết 20 tấn hàng hóa là: (xe).
Số xe lớn dự định phải dùng để chở hết 20 tấn hàng hóa là: (xe)
Vì thực tế số xe nhỏ phải dùng nhiều hơn dự định là 1 xe.
Nên ta có phương trình:
Giải phương trình:
Vậy mỗi xe nhỏ vận chuyển được 4 tấn hàng hóa.
Câu 16:
Người thứ nhất đi đoạn đường từ địa điểm A đến địa điểm B cách nhau 78km. Sau khi người thứ nhất đi được 1 giờ thì người thứ hai đi theo chiều ngược lại vẫn trên đoạn đường đó từ B về A. Hai người gặp nhau ở địa điểm C cách B một quãng đường 36km. Tính vận tốc của mỗi người, biết rằng vận tốc của người thứ hai lớn hơn vận tốc của người thứ nhất là 4km/h và vận tốc của mỗi người trong suốt đoạn đường là không thay đổi.
 Xem đáp án
Xem đáp án
Gọi vận tốc của người thứ nhất là x (km/h) (Đk: x > 0)
Khi đó, vận tốc của người thứ hai là x + 4 (km/h)
Thời gian người thứ nhất đi từ A đến C là: (giờ)
Thời gian người thứ hai đi từ B đến C là: (giờ)
Do người thứ nhất đi trước người thứ hai 1 giờ, nên khi hai người gặp nhau tại C thì ta có phương trình:
(1)
Giải phương trình (1) và kết hợp với ĐK x > 0, ta được: x = 14 (km/h)
Vậy, vận tốc của người thứ nhất là 14 (km/h) và vận tốc của người thứ hai là 14 + 4 = 18 (km/h)
Câu 17:
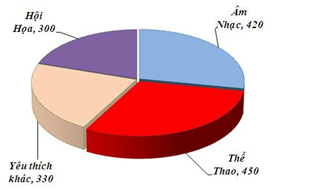
Trường A tiến hành khảo sát 1500 học sinh về sự yêu thích hội hoạ, thể thao, âm nhạc và các yêu thích khác. Mỗi học sinh chỉ chọn một yêu thích. Biết số học sinh yêu thích hội họa chiếm tỉ lê ̣20% so với số học sinh khảo sát.
Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là 30 học sinh; số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và yêu thích khác.
a)Tính số học sinh yêu thích hội họa.
b)Hỏi tổng số học sinh yêu thích thể thao và âm nhạc là bao nhiêu?
 Xem đáp án
Xem đáp án
Số học sinh yêu thích hội họa chiếm 20% số học sinh toàn trường nên số học sinh yêu thích hội họa là học sinh
Gọi số học sinh yêu thích thể thao, âm nhạc và yêu thích khác lần lượt là a; b; c
Ta có (1)
Số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và yêu thích khác nên (2)
Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là 30 nên ta được a - b = 30 (3)
(Tìm các mối quan hệ giữa các biến)
Thay (2) vào phương trình (1) ta được
Thay vào phương trình (3)
Vậy tổng số học sinh yêu thích thể thao và âm nhạc là a + b = 870
(học sinh có thể lập hệ phương trình rồi giải bằng máy tính)
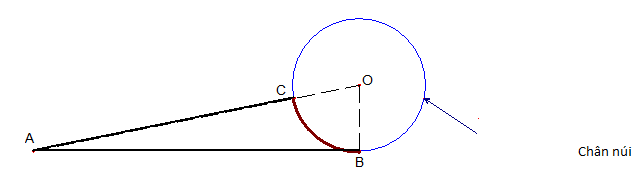
Câu 18:
Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O, bán kính 3 km) và một trạm cứu hộ ở vị trí A (tham khảo hình vẽ). Do chưa biết đường đi nào để đến vị trí tai nạn nhanh hơn nên đội cứu hộ quyết định điều hai xe cứu thương cùng xuất phát ở trạm đến vị trí tai nạn theo hai cách sau:
Xe thứ nhât : đi theo đường thẳng từ A đến B, do đường xấu nên vận tốc trung bình của xe là 40 km/h.
Xe thứ hai: đi theo đường thẳng từ A đến C với vận tốc trung bình 60 km/h, rồi đi từ C đến B theo đường cung nhỏ CB ở chân núi với vận tốc trung bình 30 km/h ( 3 điểm A, O, C thẳng hàng và C ở chân núi). Biết đoạn đường AC dài 27 km và .
a) Tính độ dài quãng đường xe thứ nhất đi từ A đến B.
b) Nếu hai xe cứu thương xuất phát cùng một lúc tại A thì xe nào thì xe nào đến vị trí tai nạn trước ?
 Xem đáp án
Xem đáp án
a) OA = AC + R = 27 + 3 = 30 km
Xét vuông tại B, có:
b) t/gian xe thứ nhất đi từ A đến B là: (giờ)
t/gian xe thứ hai đi từ A đến C là: (giờ)
Xét vuông tại B, có:
Độ dài đoạn đường từ C đến B là
T/gian đi từ C đến B là : giờ
Suy ra thời gian xe thứ hai đi từ A đến B là : 0,45 + 0,15 = 0,6 giờ
Vậy xe thứ hai đến điểm tai nạn trước xe thứ nhất.
Câu 19:
Nông trường cao su Minh Hưng phải khai thác 260 tấn mũ trong một thời gian nhất định. Trên thực tế, mỗi ngày nông trường đều khai thác vượt định mức 3 tấn. Do đó, nông trường đã khai thác được 261 tấn và song trước thời hạn 1 ngày. Hỏi theo kế hoạch mỗi ngày nông trường khai thác được bao nhiêu tấn mũ cao su.
 Xem đáp án
Xem đáp án
Gọi số tấn mũ cao su mỗi ngày nông trường khai thác được là x (tấn)
(Điều kiện: 0 < x < 260)
Thời gian dự định khai thác mũ cao su của nông trường là: (ngày)
Trên thực tế, mỗi ngày nông trường khai thác được: x + 3 (tấn)
Thời gian thực tế khai thác mũ cao su của nông trường là: (ngày)
Theo đề bài, ta có phương trình:
Phương trình (1) có 2 nghiệm phân biệt:
(nhận) hoặc (loại)
Vậy theo kế hoạch, mỗi ngày nông trường cao su khai thác 26 tấn.
Câu 20:
Hai đội công nhân cùng làm chung trong 4 giờ thì hoàn thành được công việc. Nếu làm riêng thì thời gian hoàn thành công việc đội thứ hai ít hơn đội thứ nhất là 5 giờ. Hỏi nếu làm riêng thì thời gian hoàn thành công việc của mỗi đội là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi thời gian đội thứ nhất làm riêng hoàn thành công việc là x (giờ, x > 5).
Thời gian đội thứ hai làm riêng hoàn thành công việc là y (giờ, y > 0).
Mỗi giờ đội thứ nhất làm được công việc, đội thứ hai làm được công việc.
Trong 4 giờ đội thứ nhất làm được công việc, đội thứ hai làm được công việc.
Theo đề ta có hệ phương trình
thế vào (1) ta được
Vậy nếu làm riêng thì thời gian hoàn thành công việc của đội thứ nhất là 15 giờ, đội thứ hai là 10 giờ.
Câu 21:
Đầu năm học, Hội khuyến học của một tỉnh tặng cho trường A tổng số 245 quyển sách gồm sách Toán và sách Ngữ văn. Nhà trường đã dùng số sách Toán và số sách Ngữ văn đó để phát cho các bạn học sinh có hoàn cảnh khó khăn. Biết rằng mỗi bạn nhận được một quyển sách Toán và một quyển sách Ngữ văn. Hỏi Hội khuyến học tỉnh đã tặng cho trường A mỗi loại sách bao nhiêu quyển?
 Xem đáp án
Xem đáp án
Gọi số sách Toán và sách Ngữ văn Hội khuyến học trao cho trường A lần lượt là x, y (quyển), .
Vì tổng số sách nhận được là 245 nên x + y = 245 (1)
Số sách Toán và Ngữ văn đã dùng để phát cho học sinh lần lượt là và (quyển)
Ta có:
Đưa ra hệ .
Giải hệ được nghiệm
Kết luận: Hội khuyến học trao cho trường 140 quyển sách Toán và 105 quyển sách Ngữ văn
Câu 22:
An đếm số bài kiểm tra một tiết đạt điểm 9 và điểm 10 của mình thấynhiều hơn 16 bài. Tổng số điểm của tất cả các bài kiểm tra đạt điểm 9 và điểm 10 đó là 160. Hỏi An được bao nhiêu bài điểm 9 và bao nhiêu bài điểm 10?
 Xem đáp án
Xem đáp án
Gọi số bài điểm 9 và điểm 10 của An đạt được lần lượt là x, y (bài) .
Theo giả thiết x + y > 16.
Vì tổng số điểm của tất cả các bài kiểm tra đó là 160 nên 9x + 10y = 160.
Ta có .
Do và nên x + y = 17.
Ta có hệ (thỏa mãn).
Vậy An được 10 bài điểm 9 và 7 bài điểm 10.
Câu 23:
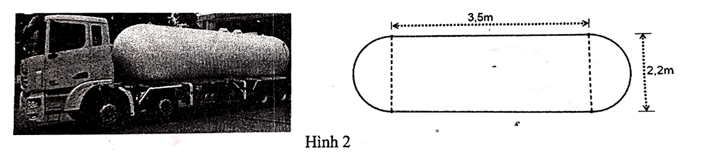
 Xem đáp án
Xem đáp án
Vkhối cầu =
Vkhối trụ =
Thể tích của bồn chứa là:
Câu 24:
Sau Kỳ thi tuyển sinh vào lớp 10 năm học 2019-2020, học sinh hai lớp 9A và 9B tặng lại thư viện trường 738 quyển sách gồm hai loại sách giáo khoa và sách tham khảo. Trong đó, mỗi học sinh lớp 9A tặng 6 quyển sách giáo khoa và 3 quyển sách tham khảo; mỗi học sinh lớp 9B tặng 5 quyển sách giáo khoa và 4 quyển sách tham khảo. Biết số sách giáo khoa nhiều hơn số sách tham khảo là 166 quyển. Tính số học sinh của mỗi lớp.
 Xem đáp án
Xem đáp án
Gọi x, y lần lượt là số học sinh lớp 9A, 9B
Theo đề bài ta có hệ pt:
Vậy số học sinh của lớp 9A là 42; của lớp 9B là 40.
Câu 25:
Đề chuẩn bị tốt cho việc tham gia kỳ thi Tuyển sinh vào lớp 10 THPT, bạn An đến của hàng sách mua thêm 1 bút bi để làm bài tự luận và 1 bút chì để làm bài trắc nghiệm khách quan. Bạn An trả cho của hàng hết 30000 đồng khi mua hai cây bút trên. Mặt khác, người bán hàng cho biết tổng số tiền thu được khi bán 5 bút bi và 3 bút chì bằng với tổng số tiền thu được khi bán 2 bút bi và 5 bút chì. Giá bán của mỗi bút bi và mỗi bút chì lần lượt là
 Xem đáp án
Xem đáp án
Gọi gia bán của một bút bi và một bút chì lần lượt là x và y (đồng) với 0 < x, y < 30000
Số tiền khi mua 1 bút bi và 1 bút chì: x + y = 30000
Số tiền 5 bút bi và 3 bút chì bằng 2 bút bi và 5 bút chì:
Giải hệ phương trình
Vậy giá mỗi bút bi là 12000 đồng và giá mỗi bút chì là 18000 đồng.
Câu 26:
Trong kỳ thi Tuyển sinh vào lớp 10 THPT năm 2019, tổng chỉ tiêu tuyển sinh của Trường THPT A và trường THPT B là 900 học sinh. Do cả hai trường đều có chất lượng giáo dục rất tốt nên sau khi hết hạn thời gian điều chỉnh nguyên vọng thì số lượng thí sinh đăng ký dự tuyển vào Trường THPT A và Trường THPT B tăng lần lượt là 15% và 10% so với chỉ tiêu ban đầu. Vì vậy, tổng số thí sinh đăng ký dự tuyển của cả hai trường là 1010. Hỏi số lượng thí sinh đăng ký dự tuyển của mỗi trường là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi x, y (thí sinh) lần lượt là chỉ tiêu của trường THPT A và THPT B và
Tổng chỉ tiêu tuyển sinh của Trường THPT A và trường THPT B là 900 học sinh:
x + y = 900 (1)
Số thí sinh thí sinh đăng ký dự tuyển vào Trường THPT A là (thí sinh)
Số thí sinh thí sinh đăng ký dự tuyển vào Trường THPT A là (thí sinh)
Tổng số thí sinh đăng ký dự tuyển của cả hai trường là 1010
Từ (1) và (2) ta có hệ phương trình
Số thí sinh thí sinh đăng ký dự tuyển vào Trường THPT A là thí sinh.
Số thí sinh thí sinh đăng ký dự tuyển vào Trường THPT A là thí sinh.
Câu 27:
Hai đội công nhân cùng làm chung một công việc thì sau 15 ngày làm xong. Nếu đội thứ nhất làm riêng trong 3 ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong 5 ngày thì cả hai đội hoàn thành được 25% công việc. Hỏi mỗi đội làm riêng thì bao nhiêu ngày mới hoàn thành xong công việc trên.
 Xem đáp án
Xem đáp án
- Gọi thời gian để đội thứ nhất và đội thứ hai làm riêng một mình hoàn thành xong công việc lần lượt là x và y (x > 15, y > 15), đơn vị (ngày).
Một ngày đội thứ nhất làm được (công việc).
Một ngày đội thứ hai làm được (công việc).
- Vì hai đội cùng làm trong 15 ngày thì hoàn thành xong công việc. Như vậy trong một ngày cả hai đội làm được (công việc). Suy ra, ta có phương trình : (1).
- Ba ngày đội đội thứ nhất làm được (công việc).
- Năm ngày đội thứ hai làm được (công việc).
- Vì đội thứ nhất làm trong 3 ngày rồi dừng lại đội thứ hai làm tiếp trong 5 ngày thì cả hai đội hoàn thành xong (công việc). Suy ra, ta có phương trình : (2).
- Từ (1) và (2) ta có hệ phương trình : (TMĐK).
- Vậy thời gian để đội thứ nhất làm riêng một mình hoàn thành xong công việc là 24 (ngày) và thời gian để đội thứ hai làm riêng một mình hoàn thành xong công việc là 40 (ngày).
Câu 28:
Một đội xe vận tải được phân công chở 112 tấn hàng. Trước giờ khởi hành có 2 xe phải đi làm nhiệm vụ khác nên mỗi xe còn lại phải chở thêm 1 tấn hàng so với dự tính. Tính số xe ban đầu của đội xe, biết rằng mỗi xe đều chở khối lượng hàng như nhau.
 Xem đáp án
Xem đáp án
Gọi x là số xe ban đầu, với , theo dự kiến mỗi xe phải chở (tấn).
Khi khởi hành số xe còn lại x - 2 và mỗi xe phải chở (tấn).
Theo bài toán ta có phương trình:
Đối chiếu điều kiện và kết luận số xe ban đầu là 16 (xe).
Câu 29:
Một đội xe vận tải được phân công chở 144 tấn hàng. Trước giờ khởi hành có 2 xe phải đi làm nhiệm vụ khác nên mỗi xe còn lại phải chở thêm 1 tấn hàng so với dự tính. Tính số xe ban đầu của đội xe, biết rằng mỗi xe đều chở khối lượng hàng như nhau.
 Xem đáp án
Xem đáp án
Gọi x là số xe ban đầu, với , theo dự kiến mỗi xe phải chở (tấn) .
Khi khởi hành số xe còn lại x - 2 và mỗi xe phải chở (tấn).
Theo bài toán ta có phương trình:
Đối chiếu điều kiện và kết luận số xe ban đầu là 18 (xe).
Câu 30:
Bác Bình dự định trồng 300 cây cam theo nguyên tắc trồng thành các hang, mỗi hang có số cây bằng nhau. Nhưng khi thực hiện bác Bình đã trồng thêm 2 hàng, mỗi hang thêm 3 cây so với dự kiến ban đầu nên trồng được tất cả 391 cây. Tính số cây trên 1 hàng mà bác Bình dự kiến trồng ban đầu.
 Xem đáp án
Xem đáp án
Gọi số cây trong một hang dự kiến ban đầu là x (cây, x )
Số hang dự kiến ban đầu là y (hàn; y ).
.Từ giả thiết ta có hệ phương trình
.
Câu 31:
Theo kế hoạch, một xưởng may phải may xong 360 bộ quần áo trong một thời gian quy định. Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 4 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch. Vì thế xưởng đã hoàn thành kế hoạch trước 1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may bao nhiêu bộ quần áo?
 Xem đáp án
Xem đáp án
Gọi số bộ quần áo mỗi ngày xưởng phải may theo kế hoạch là x
ĐK: .
Thời gian may xong 360 bộ quần áo theo kế hoạch là (ngày)
Thực tế, mỗi ngày xưởng may được x + 4 bộ quần áo
Thời gian may xong 360 bộ quần áo theo thực tế là (ngày)
Vì xưởng đã hoàn thành kế hoạch trước 1 ngày nên ta có phương trình:
Giải phương trình được: x1 = 36 (thỏa mãn ĐK)
Vậy theo kế hoạch, mỗi ngày xưởng phải may 36 bộ quần áo.
Câu 32:
Cho một thửa ruộng hình chữ nhật, biết rằng nếu chiều rộng tăng thêm 2m chiều dài giảm đi 2m thì diện tích thửa ruộng đó tăng thêm và nếu chiều rộng giảm đi 2m chiều dài tăng thêm 5m thì diện tích thửa ruộng giảm đi . Tính diện tích thửa ruộng trên.
 Xem đáp án
Xem đáp án
Gọi chiều dài thửa ruộng là x (m) chiều rộng thửa ruộng là y (m). Điều kiện x > 2, y > 2, x > y .
Nếu chiều rộng tăng lên 2m, chiều dài giảm đi 2m thì diện tích tăng thêm 30m2 nên ta có phương trình
Nếu chiều rộng giảm đi 2m, chiều dài tăng thêm 5m thì diện tích thửa ruộng giảm đi 20m2 nên ta có phương trình .
Từ (1) và (2) ta được hệ phương trình (thỏa mãn).
Vậy diện tích hình chữ nhật là .
Câu 33:
Trung tâm thương mại VC của thành phố NT có 100 gian hàng. Nếu mỗi gian hàng của Trung tâm thương mại VC cho thuê với giá 100.000.000 đồng (một trăm triệu đồng) một năm thì tất cả các gian hàng đều được thuê hết. Biết rằng, cứ mỗi lần tăng giá 5% tiền thuê mỗi gian hàng một năm thì Trung tâm thương mại VC có thêm 2 gian hàng trống. Hỏi người quản lý phải quyết định giá thuê mỗi gian hàng là bao nhiêu một năm để doanh thu của Trung tâm thương mại VC từ tiền cho thuê gian hàng trong năm là lớn nhất?
 Xem đáp án
Xem đáp án
Gọi giá tiền mỗi gian hàng tăng lên x (triệu đồng) (ĐK: x > 0)
Khi đó giá mỗi gian hàng sau khi tăng lên là 100 + x (triệu đồng).
Cứ mỗi lần tăng 5% tiền thuê mỗi gian hàng (tăng 5%.100 = 5 triệu đồng) thì có thêm 2 gian hàng trống nên khi tăng x triệu đồng thì có thêm gia hàng trống.
Khi đó số gian hàng được thuê sau khi tăng giá là (gian).
Số tiền thu được là: (triệu đồng).
Yêu cầu bài toán trở thành tìm x để đạt giá trị lớn nhất.
Ta có:
Ta có
Dấu "=" xảy ra khi và chỉ khi x = 75.
Vậy người quản lí phải cho thuê mỗi gian hàng với giá 100 + 75 = 175 triệu đồng thì doanh thu của trung tâm thương mại VC trong năm là lớn nhất.
Câu 34:
Ông Khôi sở hữu một mảnh đất hình chữ nhật có chu vi là 100m. Ông ta định bán mảnh đất đó với giá thị trường là 15 triệu đồng cho một mét vuông. Hãy xác định giá tiền của mảnh đất đó biết rằng chiều dài gấp bốn lần chiều rộng.
 Xem đáp án
Xem đáp án
Gọi chiều rộng của mảnh đất là x (m, 0 < x < 50)
Chiều dài của mảnh đất là 4x (m).
Chi vi mảnh đất là 100m :
Vậy chiều rộng của mảnh đất là 10m, chiều dài mảnh đất là 40m.
Diện tích mảnh đất là : 40.10 = 400 m2.
Giá tiền của mảnh đất : 400x150000000 = 6000000000 đồng = 6 tỷ (đồng).
Câu 35:
Quãng đường AB dài 60km, một người đi xe đạp từ A đến B với vận tốc và thời gian quy định. Sau khi đi được nửa quãng đường người đó giảm vận tốc 5km/h trên nửa quãng đường còn lại. Vì vậy, người đó đã đến B chậm hơn quy định 1 giờ. Tính vận tốc và thời gian quy định của người đó.
 Xem đáp án
Xem đáp án
Gọi vận tốc quy định của người đó là x (km/h), (x > 5)
Thời gian quy định để người đó đi hết quãng đường là .
Nửa quảng đường đầu là: 60 : 2 = 30 (km) nên thời gian đi nửa quãng đường đầu là: .
Nửa quãng đường sau, vận tốc của người đó giảm 5km/h nên vận tốc lúc sau là: x - 5 (km/h).
Thời gian đi nửa quãng đường sau là .
Vì người đó đến chậm so với thời gian dự định là 1 giờ nên ta có phương trình:
Vậy vận tốc quy định của người đó là 15km/h và thời gian quy định của người đó là: 60 : 15 = 4 giờ.
Câu 36:
Trong lễ phát động phong trào trồng cây nhân dịp kỷ niệm ngày sinh Bác Hồ, lớp 9A được giao trồng 360 cây. Khi thực hiện có 4 bạn được điều đi làm việc khác, nên mỗi học sinh còn lại phải trồng thêm 1 cây so với dự định. Hỏi lớp 9A có bao nhiêu học sinh? (biết số cây trồng của mỗi học sinh như nhau)
 Xem đáp án
Xem đáp án
Gọi số học sinh lớp 9A là x (hs)
Suy ra số học sinh lớp 9A trên thực tế là x - 4(hs)
Số cây mỗi học sinh lớp 9A trồng theo dự định là (cây)
Số cây mỗi học sinh lớp 9A trồng trên thực tế là (cây)
Theo đề bài ta có phương trình
Vì nên x = 40
Vậy số học sinh của lớp 9A là 40 học sinh