Chuyên đề 4: Hàm số có đáp án
-
1605 lượt thi
-
56 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Chứng minh rằng parabol (P): luôn cắt đường thẳng (d): tại hai điểm phân biệt A và B. Gọi là hoành độ hai điểm A, B. Tìm m sao cho
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của P và d là:
Ta có
với mọi m
Suy ra phương trình 1 luôn có hai nghiệm phân biết với mọi m
Nên P luôn cắt d tại hai điểm phân biệt A và B
Theo vi-ét ta có:
Theo đề ta có:
Câu 2:
Cho đường thẳng d: y = ax + b. Tìm giá trị của a và b sao cho đường thẳng d đi qua điểm A(0; -1) và song song với đường thẳng .
 Xem đáp án
Xem đáp án
Ta có
Đường thẳng d: y = x + b đi qua điểm A(0; -1) nên thay x = 0; y = -1 vào phương trình đường thẳng d ta được
Vậy a = 1; b = -1.Câu 3:
Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm (atmosphere). Bên dưới mặt nước, áp suất nước tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất y (atm) và độ sâu x (m) dưới mặt nước là một hàm số bậc nhất y = ax + b.
a. Xác định các hệ số a và b.
b. Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất là 2,85atm?
 Xem đáp án
Xem đáp án
a. Do áp suất tại bề mặt đại dương là 1atm, nên y = 1, x = 0, thay vào hàm số bậc nhất ta được:
Do cứ xuống sâu thêm 10m thì áp xuất nước tăng lên 1atm, nên tại độ sau 10m thì áp suất nước là 2atm (y = 2, x = 10), thay vào hàm số bậc nhất ta được:
Do b = 1 nên thay vào ta được .
Vì vậy, các hệ số , b = 1.
b.Từ câu a, ta có hàm số
Thay y = 2,85 vào hàm số, ta được:
Vậy khi người thợ nặn chịu một áp suất là 2,85atm thì người đó đang ở độ sâu 18,5m.
Câu 4:
Cho hàm số y = ax + b với a 0. Xác định các hệ số a, b biết đồ thị hàm số song song với đường thẳng y = 2x + 2019 và cắt trục tung tại điểm có tung độ là 2020.
 Xem đáp án
Xem đáp án
( d): y = ax + b ( a 0) song song với (∆): y = 2x + 2019
a = 2, b 2019 (1)
+ (d) cắt Oy tại điểm có tung độ 2020 b = 2020 (2)
Từ (1), (2) ta có: y = 2x + 2020
Câu 5:
Tìm tọa độ giao điểm của đường thẳng và đường thẳng .
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của và là
Với x = 2 tìm được y = 5
Vậy tọa độ giao điểm của và là (2; 5).
Câu 6:
Trong các hàm số sau, hàm số nào đồng biến trên ?
 Xem đáp án
Xem đáp án
Hàm số y = 2x - 3 đồng biến trên ![]() .
.
Câu 7:
Cho hàm số có đồ thị là Parabol (P): .
a) Vẽ đồ thị (P) của hàm số đã cho.
b) Qua điểm A(0; 1) vẽ đường thẳng song song với trục hoành Ox cắt (P) tại hai điểm E và F. Viết tọa độ của E và F.
 Xem đáp án
Xem đáp án
Bảng giá trị:

Đồ thị hình vẽ bên
Câu 8:
Trong mặt phẳng tọa độ Oxy cho ba đường thẳng
Tìm hàm số có đồ thị là đường thẳng d song song với đường thẳng đồng thời đi qua giao điểm của hai đường thẳng và .
 Xem đáp án
Xem đáp án
Phương trình đường thẳng .
Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ phương trình
Vậy phương trình đường thẳng cần tìm là d: y = -3x + 4.
Câu 10:
Cho hàm số y = ax - 2 có đồ thị là đường thẳng (d) như hình vẽ bên dưới. Hệ số góc của đường thẳng (d) bằng
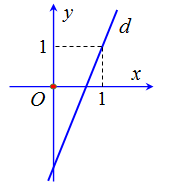
 Xem đáp án
Xem đáp án
Chọn A
Từ hình vẽ ta thấy (d) đi qua điểm (1; 1) nên:
Vậy hệ số góc của (d) là a = 3.
Câu 11:
 Xem đáp án
Xem đáp án
Vì đường thẳng (d) song song với đường thẳng y = -3x + 2019 nên .
.
(thỏa mãn).
Câu 13:
Cho điểm A(a; b) là giao điểm của hai đường thẳng (d) và (l) như hình vẽ bên.
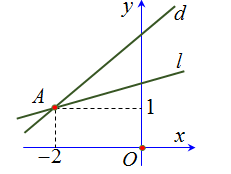
Cặp số (a; b) là nghiệm của hệ phương trình nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D
Dựa hình vẽ, giao điểm của đường thẳng (d) và (l) là A(-2; 1)
HPT có nghiệm là (-1; 2).
HPT có nghiệm là (1; -2).
HPT có nghiệm là (18; 9).
HPT có nghiệm là (-2; 1).
Câu 14:
Cho đường thẳng song song với đường thẳng và cắt trục tung tại điểm A(0; 3). Giá trị của biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn C
Vậy
Câu 15:
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình: . Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung; H là trung điểm của đoạn thẳng AB. Tính độ dài các đoạn thẳng OH (đơn vị đo trên các trục tọa độ là xentimét).
 Xem đáp án
Xem đáp án
. Do đó, giao điểm của d với trục hoành là .
. Do đó, giao điểm của d với trục tung là .
(cm).
Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
(cm)
(cm).
Câu 16:
Tìm các giá trị của a và b để đường thẳng (d): y = ax + b đi qua hai điểm M(1; 5) và N(2; 8).
 Xem đáp án
Xem đáp án
Do đường thẳng (d) qua điểm M(1; 5) nên ta có: a + b = 5
(d) qua điểm N(2; 8) ta có: 2a + b = 8
a, b là nghiệm của hệ
Câu 17:
Cho đường thẳng (d): y = 2x – 2
a) Vẽ đường thẳng (d) trong hệ trục tọa độ Oxy.
b) Tìm m để đường thẳng (d’): y = (m - 1)x + 2m song song với đường thẳng (d)
 Xem đáp án
Xem đáp án
Tìm được giao điểm của (d) với Ox và Oy lần lượt tại A(1;0) và B(0;-2)
Vẽ được đường thẳng (d).
.(d) // (d’) .
Câu 18:
Tìm giá trị của m để đường thẳng (d): y = mx + 3 đi qua điểm A(1;5)
 Xem đáp án
Xem đáp án
Đường thẳng (d): y = mx +3 đi qua điểm A(1;5) nên ta có:
5 = m.1 + 3 ó m = 2
Vậy với m = 2 thì đường thẳng (d): y = mx + 3 đi qua điểm A(1;5).
Câu 19:
Cho hai đường thẳng (d1): y = 2x - 5 và (d2): y = 4x - m (m là tham số). Tìm tất cả các giá trị của tham số m để (d1) và (d2) cắt nhau tại một điểm trên trục hoành Ox.
 Xem đáp án
Xem đáp án
Thay y = 0 vào phương trình y = 2x – 5 được:
2x – 5 = 0 x = 2,5
(d1) và (d2) cắt nhau tại một điểm trên trục hoành Ox
(d2) đi qua điểm
4. 2,5 – m = 0
m = 10
Vậy m = 10 là giá trị cần tìm.
Câu 20:
Tìm các giá trị của tham số m để đồ thị hai hàm số y = (m + 4)x + 11 và cắt nhau tại một điểm trên trục tung.
 Xem đáp án
Xem đáp án
Do hai đồ thị hàm số cắt nhau tại một điểm trên trục tung nên .
.
Câu 22:
Viết phương trình đường thẳng AB, biết A(-1; 4) và B(5; 2)
 Xem đáp án
Xem đáp án
Phương trình đường thẳng AB có dạng (d): y = ax + b
Phương trình (d) đi qua A(-1; -4) : -a + b = -4 (1)
Phương trình (d) đi qua B(5; 2) : 5a + b = 2 (2)
Từ (1) và (2) ta có hệ phương trình
Vậy phương trình đường thẳng AB có dạng y = x - 3
Câu 23:
Cho hàm số ( m là tham số)
a).Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên ![]() .
.
b).Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol tại hai điểm phân biệt. Gọi , là hoành độ các giao điểm, tìm m sao cho .
c).Gọi đồ thị hàm số đã cho là đường thẳng (d). Chứng minh khoảng cách từ điểm O(0; 0) đến (d) không lớn hơn .
 Xem đáp án
Xem đáp án
a)
đồng biến trên .
Vậy m > 4 thì hàm số đồng biến trên .
b)
.
Phương trình hoành độ giao điểm của (d), (P):
, Có
Có
Do có
Suy ra (d) cắt luôn cắt (P) tại hai điểm phân biệt .
Có
, mà
.
Vậy m = 5, m = 2 thỏa yêu cầu bài
c)
*Trường hơp 1: Xét , thì (d): y = 8, (d) song song trục Ox, (d) cắt trục Oy tại B(0; 8)
Có khoảng cách từ O đến đường thẳng (d) là OB = 8
Gọi H là hình chiếu của O lên đường thẳng (d).
vuông tại O có , Có OH.AB = OA.OB
Giả sử
(sai)
Vậy .
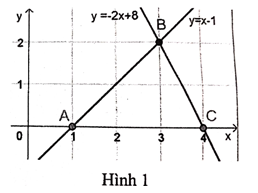
Câu 24:
Hai đường thẳng y = x - 1 và y = -2x + 8 cắt nhau tại điểm B và lần lượt cắt trục Ox tại điểm A, C (hình 1). Xác định tọa độ các điểm A, B, C và tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
(đvdt)
Câu 25:
Xác định hàm số bậc nhất y = ax + b, biết rằng đồ thị hàm số đi qua điểm M(1; -1) và N(2; 1).
 Xem đáp án
Xem đáp án
Vì đồ thị hàm số đi qua điểm M(1; -1) nên a + b = -1
đồ thị hàm số đi qua điểm N(2; 1) nên 2a + b = 1
Yêu cầu bài toán
Vậy hàm số phải tìm là y = 2x - 3.
Câu 26:
Tìm tọa độ giao điểm của hai đường thẳng .
 Xem đáp án
Xem đáp án
Tọa độ giao điểm của hai đường thằng là nghiệm của hệ phương trình
Câu 27:
Cho đường thẳng (d): y = ax + b. Tìm a, b để đường thẳng (d) song song với đường thẳng (d'): y = 5x + 6 và đi qua điểm A(2; 3)
 Xem đáp án
Xem đáp án
Vì (d) // (d') nên
Vì (d) đi qua A(2; 3) nên ta có:
Vậy a = 5; b = 7 ta có
Câu 28:
Trong mặt phẳng tọa độ Oxy, cho hàm số có đồ thị (P).
a) Vẽ đồ thị (P).
b) Tìm giá trị của m để đường thẳng (d): y = 2x - 3m (với m là tham số) cắt (P) tại hai điểm phân biệt có hoành độ là thỏa mãn
 Xem đáp án
Xem đáp án
a) Bảng giá trị của hàm số

Vẽ đường cong đi qua các điểm có tọa độ ta được parabol (P):
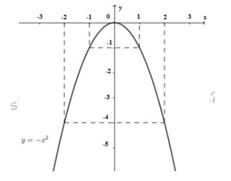
b)
Xét phương trình hoành độ giao điểm của đường thẳng (d) và parabol (P), ta có
(*)
Phương trình (*) có
Để đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành độ là thì phương trình (*) có hai nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Theo bài ra ta có:
Vậy m = 1 là giá trị cần tìm.
Câu 29:
Điểm nào sau đây là giao điểm của đường thẳng (d): y = 2x + 3 và parabol
 Xem đáp án
Xem đáp án
Chọn A
Phương trình hoành độ giao điểm của (P) và (d) là
Giao điểm cần tìm là (-2; -1) và (6; -9).
Câu 31:
Trong mặt phẳng toạ độ Oxy, cho parabol và đường thẳng (m là tham số thực). Tìm các giá trị của m để (d) và (P) cắt nhau tại hai điểm phân biệt thoả mãn điều kiện
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (P) và (d) là
(P) và (d) cắt nhau tại hai điểm phân biệt khi phương trình (*) có 2 nghiệm phân biệt
với mọi
Ta có là giao điểm của (P) và (d) nên với là hai nghiệm của phương trình (*)
Áp dụng định lý Vi – et đối với (*):
Theo đề bài ta có
Vậy m = 0 hoặc m = 2 thoả mãn yêu cầu bài toán.
Câu 32:
Xác định hệ số a của hàm số , biết đồ thị của hàm số đó đi qua điểm A(-3; 1).
 Xem đáp án
Xem đáp án
Đồ thi hàm số đi qua điểm A(-3; 1) khi và chỉ khi
.
Câu 33:
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình và đường thẳng (d) có phương trình (với m là tham số).
a) Tìm tọa độ điểm M thuộc parabol (P), biết điểm M có hoành độ bằng 4.
b) Chứng minh đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt. Gọi lần lượt là hoành độ của hai điểm A, B. Tìm m để .
 Xem đáp án
Xem đáp án
a) Vì .
b) Phương trình hoành độ giao điểm của (P) và (d) là
Ta có
Suy ra đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt.
Ta có hệ thức Vi-ét
Yêu cầu
Vậy m = 1.
Câu 34:
Trong mặt phẳng tọa độ Oxy, cho đường thẳng và parabol
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt
b) Tìm tất cả giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ thỏa mãn
 Xem đáp án
Xem đáp án
a) Xét phương trình hoành độ giao điểm
Để (d) luôn cắt (P) tại hai điểm phân biệt thì phương trình (1) có hai nghiệm phân biệt với
Ta có :
Xét
Vậy (d) luôn cắt (P) tại hai điểm phân biệt
b) Tìm tất cả giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ thỏa mãn
Ta có
Hai nghiệm của phương trình :
Biến đổi biểu thức (2) ta có :
Thay vào biểu thức ta có :
Kết Luận : Với m = 3 thỏa mãn yêu cầu bài toán.
Câu 35:
Trong mặt phẳng tọa độ Oxy cho parabol (P):
a) Vẽ parapol (P)
b) Tìm m để đường thẳng (d): đi qua điểm M(1; -1)
 Xem đáp án
Xem đáp án
a) Tự vẽ
b)
Vì M(1; -1) thuộc (d): nên thay tọa độ M vào d ta được:
Vậy m = 0; m = -4 thỏa mãn bài toán
Câu 36:
Cho đường thẳng (d): y = x - 1 và parabol (P):
a) Tìm tọa độ A thuộc parabol (P) biết điểm A có hoành độ x = -1
b) Tìm b để đường thẳng (d) và đường thẳng (d’): cắt nhau tại một điểm trên trục hoành.
 Xem đáp án
Xem đáp án
a) Điểm A có hoành độ x = -1 và thuộc P nên thay x = -1 vào P ta được :
b) Gọi là điểm thuộc trục hoành và là giao điểm của hai đường thẳng d, d’. ta có thuộc d
Lại có:Câu 37:
Cho parabol và đường thẳng (x là ẩn, m tham số).
a) Tìm tọa độ giao điểm của parabol (P) với đường thẳng (d) khi m = 4.
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt thỏa mãn .
 Xem đáp án
Xem đáp án
a. Khi m = 4, đường thẳng (d) có dạng: y = -x + 4.
Xét phương trình hoành độ giao điểm của (d) và (P): (1)
PT (1) có
PT (1) có hai nghiệm phân biệt :
Với
Với
Vậy, khi m = 4 thì đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt có tọa độ lần lượt là (-4; 8) và (2; 2)
b. Xét phương trình hoành độ giao điểm của (d) và (P): (2)
PT (2) có
Để (d) cắt (P) tại hai điểm phân biệt thì PT (2) phải có hai nghiệm phân biệt.
hay (*)
Với ĐK (*) , gọi là hai nghiệm của PT (2).
Áp dụng định lí Viets, ta có : (3)
Với
Với
Xét biểu thức :
(4)
Thay (3) vào (4), ta được :
Vậy, với thì yêu cầu bài toán được thỏa mãn.
Câu 38:
Cho Parabol và đường thẳng (d): y = 3x - 1. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (P) và (d) là:
Vậy tọa độ giao điểm của (P) và (d) là A(1; 2) và ![]()
Câu 39:
a) Vẽ đồ thị (P) của hàm số
b)Tìm giao điểm của đồ thị hàm số (P) với đường thẳng (d): y = x
 Xem đáp án
Xem đáp án
a)
Ta có bảng giá trị sau
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
2 |
|
0 |
|
2 |
Đồ thị hàm số là đường cong đi qua các điểm (-2;2); (-1; ); (0;0); (1; ); (2;2) và nhận trục Oy làm trục đối xứng.
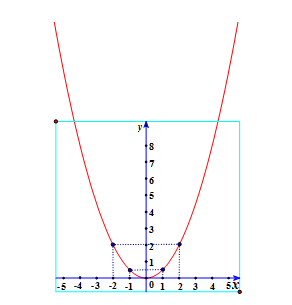
b) Xét phương trình hoành độ giao điểm của đồ thị hàm số (P) và đường thẳng (d):
Với x = 0 => y = 0 ta có giao điểm O(0;0)
Với x = 2 => y = 2 ta có giao điểm A(2;2)
Vậy giao điểm của đồ thị hàm số (P) và đường thẳng (d) là O(0;0); A(2;2)
Câu 40:
Cho Parabol và đường thẳng (d): y = 3x + 2.
a) Vẽ đồ thị (P) trên hệ trục tọa độ Oxy;
b) Tìm tọa độ giao điểm của (P) và (d).
 Xem đáp án
Xem đáp án
a) Bảng giá trị :
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
|
8 |
2 |
0 |
2 |
8 |
Đồ thị hàm số là một đường cong đi qua các điểm:
Đồ thị như hình vẽ :
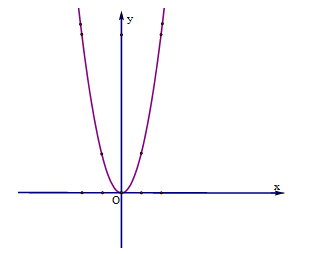
b) Phương trình hoành độ giao điểm của (P) và (d) :
(*)
Ta có = (-3)2 – 4.2.(-2) = 25 > 0
Phương trình (*) có hai nghiệm : hoặc x = 2
Khi thì y = ta được giao điểm
Khi x = 2 thì y = ta được giao điểm (2; 8)
Vậy giao điểm của (P) và (d) là và (2; 8)
Câu 41:
Cho Parabol và đường thẳng (d): y = x - 2
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ Oxy.
b) Viết phương trình đường thẳng (d')song song với (d) và tiếp xúc với (P).
 Xem đáp án
Xem đáp án
a)
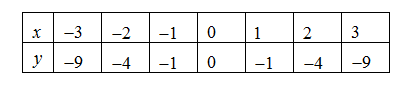
(d): y = x - 2
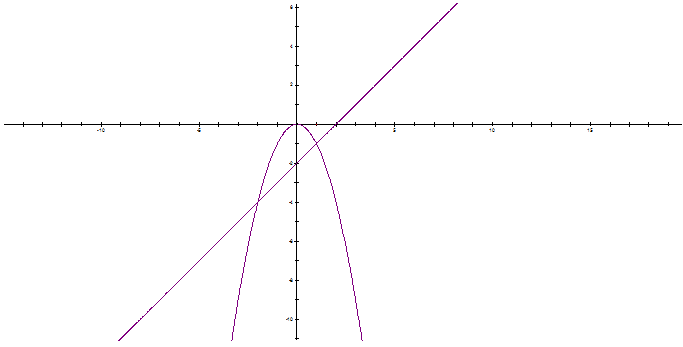
b) Phương trình đường thẳng (d') có dạng y = ax + b
Phương trình hoành độ giao điểm của (P) và (d') là
PT (*) có .
Vậy PT đường thẳng
Câu 42:
Trong mặt phẳng tọa độ Oxy , cho parabol .
a) Vẽ parabol (P)
b) Hai điểm A, B thuộc (P) có hoành độ lần lượt là 2; -1. Viết phương trình đường thẳng đi qua hai điểm A và B.
 Xem đáp án
Xem đáp án
Gọi phương trình đường thẳng cần tìm là: y = ax + b
Vì thuộc đường thẳng y = ax + b nên:
Vậy đường thẳng cần tìm là: y = 2x - 2
Câu 43:
Tìm tọa độ giao điểm của đồ thị hàm số và đồ thị hàm số y = 3x - 2
 Xem đáp án
Xem đáp án
Hoành độ giao điểm của đồ thị hai hàm số đã cho là nghiệm của PT:
Giải được hai nghiệm:
Từ đó tìm được hai giao điểm có tọa độ là: (1; 1) và (2; 4)
Câu 44:
Cho parabol (P): và đường thẳng (m là tham số, ).
a) Xác định tất cả các giá trị của m để đường thẳng (d) đi qua điểm I (1; 3).
b) Tìm m để parabol (P) cắt đường thẳng (d) tại hai điểm phân biệt A, B. Gọi là hoành độ hai điểm A, B; tìm m sao cho .
 Xem đáp án
Xem đáp án
a)
Để đường thẳng (d): đi qua điểm I (1;3) thì x = 1; y = 3 thỏa mãn phương trình đường thẳng (d) nên ta có:
Vậy với m = 1 hoặc m = - 5 thì đường thẳng (d) đi qua điểm I(1;3)
b)
(P): và (d):
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:
với mọi m
Phương trình (1) luôn có hai nghiệm phân biệt với mọi m
Khi đó theo hệ thức Vi-ét:
Theo bài ra, ta có:
Thay (2) vào (3) ta có:
Vậy m = 168 thỏa mãn bài.
Câu 45:
Cho parabol và đường thẳng (d): y = x - 4.
a. Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
 Xem đáp án
Xem đáp án
a. Hàm số có tập xác định D = R
Bảng giá trị

* Hàm số y = x - 4 có tập xác định: D = R
Bảng giá trị
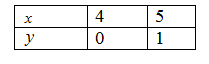
Hình vẽ:
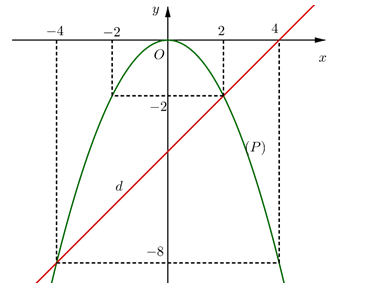
b. Phương trình hoành độ gia điểm của (P) và (d):
Vậy (P) cắt (d) tại hai điểm có tọa độ lần lượt là (2; -2) và (-4; -8).
Câu 46:
Tìm các giá trị của m để hàm số y = (2m – 1)x2 đạt giá trị lớn nhất bằng 0 tại x = 0.
 Xem đáp án
Xem đáp án
Hàm số y = (2m – 1)x2 đạt giá trị lớn nhất tại x = 0.
Khi 2m – 1 < 0 m <
Câu 47:
Cho hai hàm số y = x - 3 và có đồ thị lần lượt là (d) và (P)
1. Vẽ (d) và (P) trên cùng hệ trục tọa độ Oxy
2. Tìm tọa độ giao điểm của (d) và (P) bằng phép toán
 Xem đáp án
Xem đáp án
1. Đồ thị của hàm số y = x - 3 là đường thẳng đi qua hai điểm (0; -3) và (3; 0)
Bảng giá trị của hàm số là:
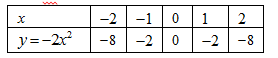
Đồ thị hàm số là Parabol đi qua các điểm (-2; -8); (-1; -2); (0; 0); (1; -2); (2; -8) nhận làm trục đối xứng.
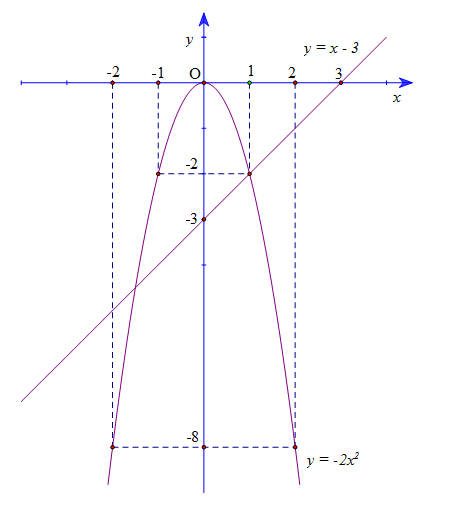
2. Xét phương trình hoành độ giao điểm của (P) và (d) là: (*)
Vì phương trình (*) có hệ số a + b + c = 0 nên có 2 nghiệm là
Với x = 1 , ta có điểm A(1; -2)
Với ta có điểm
Vậy (d) giao (P) tại hai điểm là A(1; -2) và
Câu 48:
Cho Parabol (P): và đường thẳng (d): y = x - m (với m là tham số).
a) Vẽ parabol (P).
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành độ thỏa mãn điều kiện
 Xem đáp án
Xem đáp án
a) Bảng giá trị:
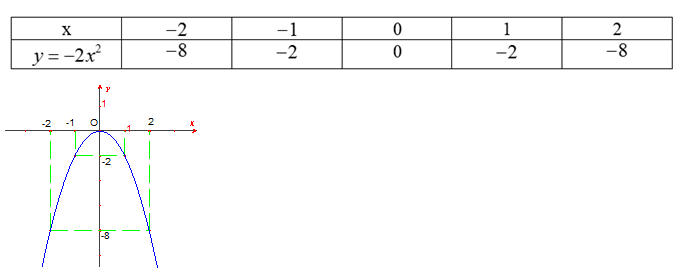
b) Phương trình hoành độ giao điểm của (P) và (d) là:
Để (d) cắt (P) tại hai điểm phân biệt
- Vì là hai nghiệm của pt hoành độ giao điểm, nên ta có:
Khi đó : (Thỏa ĐK)
Câu 49:
Tìm m để đồ thị hàm số đi qua điểm A(1; 5).
 Xem đáp án
Xem đáp án
A(1; 5) thuộc đồ thị hàm số suy ra
5 = 2m + 1
Vậy m = 2 là giá trị cần tìm.
Câu 50:
 Xem đáp án
Xem đáp án
Bảng sau cho một số giá trị tương ứng của x và y

Vẽ đồ thị:
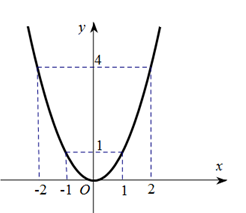
Câu 51:
Cho hàm số . Điểm M(1; 2) thuộc đồ thị hàm số khi
 Xem đáp án
Xem đáp án
Chọn A
Vì M(1; 2) thuộc đồ thị hàm số nên ta có (thỏa mãn).
Câu 52:
Cho Parabol và đường thẳng (d): y = x + m - 1 ( là tham số)
1) Vẽ đồ thị (P)
 Xem đáp án
Xem đáp án
1) Ta có bảng giá trị

Vậy đồ thị hàm số là đường cong đi qua các điểm như bảng
Đồ thị hàm số

2)
Ta có phương trình hoành độ giao điểm của hai đồ thị hàm số (d) và (P) là:
(*)
Theo đề bài ta có: (d) cắt (P) tại hai điểm phân biệt
(*) có hai nghiệm phân biệt
Vậy với thì phương trình (*) có hai nghiệm phân biệt.
Áp dụng hệ thức Vi-et ta có:
Theo đề bài ta có:
Kết hợp các điều kiện của m ta được
Vậy thoả mãn bài toán.
Câu 53:
Cho parabol và đường thẳng (d): y = x + 2.
a) Vẽ parabol (P) và đường thẳng (d) trên cùng hệ trục tọa độ Oxy .
b) Viết phương trình đường thẳng song song với (d) và cắt (P) tại điểm A có hoành độ bằng -2.
 Xem đáp án
Xem đáp án
a) Đồ thị hàm số là đường Parabol đi qua các điểm và nhận Oy làm trục đối xứng.
Đồ thị hàm số y = x + 2 là đường thẳng đi qua điểm (0; 2) và điểm (-2; 0)

b)
Vì đường thẳng song song với (d) nên ta có phương trình của đường thẳng
Gọi là giao điểm của parabol (P) và đường thẳng .
Mặt khác, , thay tọa độ của điểm A vào phương trình đường thẳng , ta được: (nhận)
Vậy phương trình đường thẳng
Câu 54:
Cho hàm số có đồ thị (P) và đường thẳng (d): y = 2x + 1. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm:
Phương trình (*) có hệ số:
Phương trình (*) có hai nghiệm:
- Với
- Với
Vậy tọa độ giao điểm của (P) và (d) là A(1; 3) và .
Câu 55:
Trong mặt phẳng tọa độ Oxy, cho parabol Vẽ (P).
 Xem đáp án
Xem đáp án
Tìm được 5 cặp giá trị có
(3 cặp có cho 0,25)
Vẽ được (P) qua 5 điểm có (O)
Câu 56:
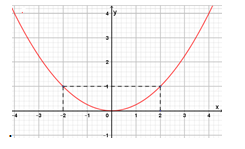
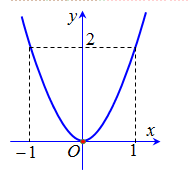
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đó là
 Xem đáp án
Xem đáp án
Đồ thị hàm số có bề lõm hướng lên và đi qua điểm (1; 2) nên a > 0 và
Vậy hàm số đó là