Trắc nghiệm Toán 9 Bài 1 (có đáp án): Một số hệ thức về cạnh và đường cao trong tam giác (phần 2)
Trắc nghiệm Toán 9 Bài 1 (có đáp án): Một số hệ thức về cạnh và đường cao trong tam giác (phần 2)
-
2517 lượt thi
-
38 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?

 Xem đáp án
Xem đáp án
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức:
HA2 = HB.HC
Đáp án cần chọn là: B
Câu 2:
“Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng…”. Cụm từ thích hợp điền vào chỗ trống là:
 Xem đáp án
Xem đáp án
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức
HA2 = HB.HC
Hay “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền”
Đáp án cần chọn là: B
Câu 3:
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?

 Xem đáp án
Xem đáp án
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức
; ; AB.AC = BC.AH và
Nhận thấy phương án D: là sai
Đáp án cần chọn là: D
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
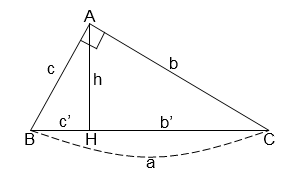
 Xem đáp án
Xem đáp án
Nhận thấy ah = bc nên phương án C là sai
Đáp án cần chọn là: C
Câu 5:
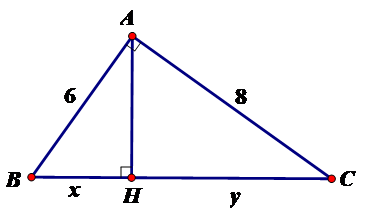
Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Theo định lý Py-ta-go ta có:
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
hay x = 3,6
=> CH = BC – BH = 10 – 3,6 = 6,4
Đáp án cần chọn là: A
Câu 6:
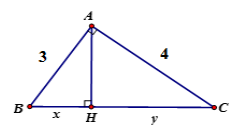
Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Theo định lý Py-ta-go ta có
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
hay x = 1,8
=> CH = BC – BH = 5 – 1,8 = 3,2 hay y = 3,2
Vậy x = 1,8; y = 3,2
Đáp án cần chọn là: B
Câu 7:
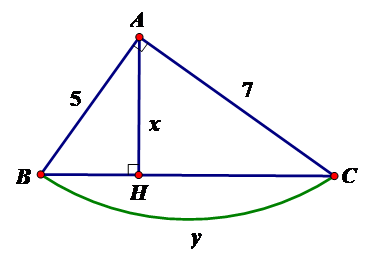
Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
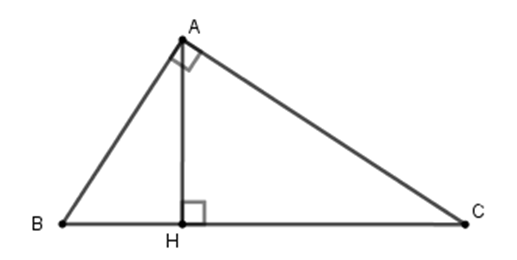
Theo định lý Py-ta-go ta có
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
BC.AH = AB.AC <=> AH =
Vậy
Đáp án cần chọn là: A
Câu 8:
Cho tam giác ABC vuông tại A, chiều cao AH và AB = 5; AC = 12. Đặt BC = y, AH = x. Tính x, y
 Xem đáp án
Xem đáp án
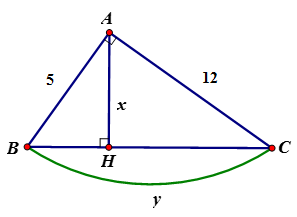
Theo định lý Py-ta-go ta có
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
BC.AH = AB.AC <=> AH =
Vậy ; y = 13
Đáp án cần chọn là: D
Câu 9:
Cho tam giác ABC vuông tại A, AH BC (H thuộc BC). Cho biết AB : AC = 3 : 4 và BC = 15cm. Tính độ dài đoạn thẳng BH
 Xem đáp án
Xem đáp án
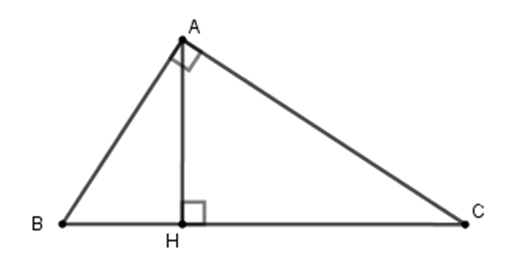
Ta có AB : AC = 3 : 4
(Vì theo định lý Py-ta-go ta có )
Nên AB = 9; AC = 12
Theo hệ thức lượng trong tam giác vuông ABC ta có:
Vậy BH = 5,4
Đáp án cần chọn là: A
Câu 10:
Cho tam giác ABC vuông tại A, AH BC (H thuộc BC). Cho biết AB : AC = 4 : 5 và BC = cm. Tính độ dài đoạn thẳng CH (làm tròn đến chữ số thập phân thứ nhất.
 Xem đáp án
Xem đáp án
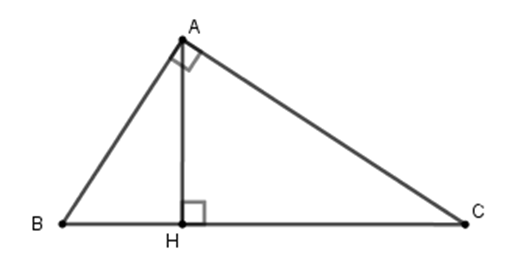
Ta có AB : AC = 4 : 5
(Vì theo định lý Py-ta-go ta có )
Nên AB = 4; AC = 5
Theo hệ thức lượng trong tam giác vuông ABC ta có:
Vậy CH 3,9
Đáp án cần chọn là: D
Câu 11:
Tìm x, y trong hình vẽ sau:
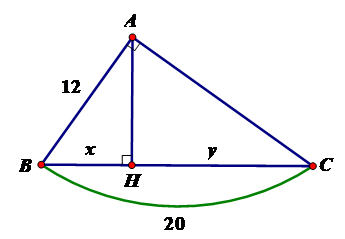
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
=> CH = BC – BH = 20 – 7,2 = 12,8
Vậy x = 7,2; y = 12,8
Đáp án cần chọn là: C
Câu 12:
Tìm x, y trong hình vẽ sau:
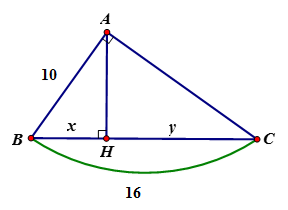
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
=> CH = BC – BH = 16 – 6,25 = 9,75
Vậy x = 6,25; y = 9,75
Đáp án cần chọn là: B
Câu 13:
Tìm x trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai).
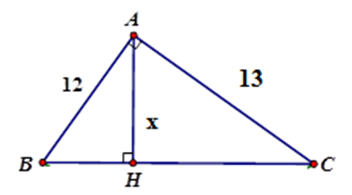
 Xem đáp án
Xem đáp án
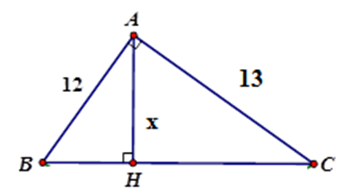
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x 8,82
Đáp án cần chọn là: B
Câu 14:
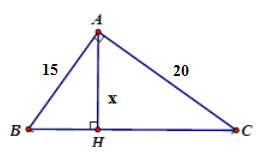
Tính x trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 12
Đáp án cần chọn là: C
Câu 15:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 4 và AH = 6cm. Tính độ dài các đoạn thẳng CH
 Xem đáp án
Xem đáp án
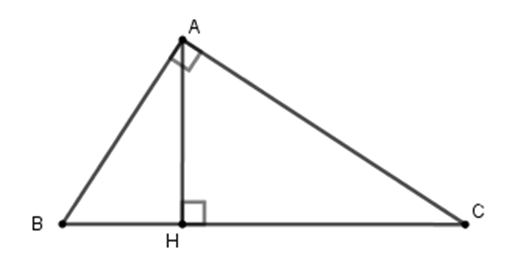
Ta có: AB : AC = 3 : 4, đặt AB = 3a; AC = 4a (a > 0)
Theo hệ thức lượng:
=> a = (TM) => AB = 7,5; AC = 10
Theo định lý Py-ta-go cho tam giác vuông AHC ta có:
CH =
Vậy CH = 8
Đáp án cần chọn là: A
Câu 16:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài các đoạn thẳng CH
 Xem đáp án
Xem đáp án
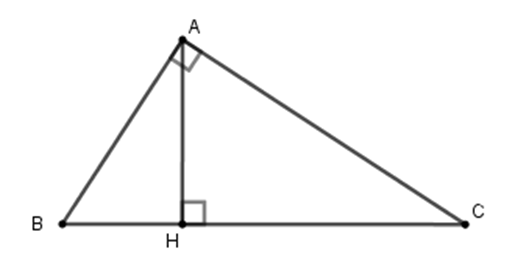
Ta có: AB : AC = 3 : 7, đặt AB = 3a; AC = 7a (a > 0)
Theo hệ thức lượng:
Theo định lý Py-ta-go cho tam giác vuông AHC ta có:
CH =
Vậy CH = 98
Đáp án cần chọn là: C
Câu 17:
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 4cm, . Tính chu vi tam giác ABC
 Xem đáp án
Xem đáp án
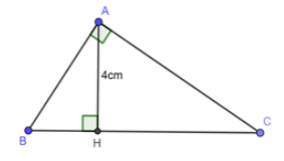
Ta có: HC = 4HB
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Ta có: BC = BH + HC = 2 + 8 = 10 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Áp dụng định lý Pitago cho ABH vuông tại A có:
Vậy chu vi tam giác ABC là:
Đáp án cần chọn là: D
Câu 18:
Cho tam giác ABC vuông tại A. Biết , đường cao AH = 42cm. Tính BH, HC
 Xem đáp án
Xem đáp án
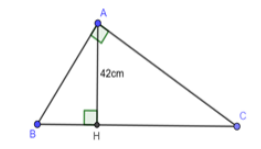
Ta có:
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AC = (cm), AB = = (cm)
Áp dụng định lý Pytago cho ABH vuông tại A có:
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Đáp án cần chọn là: A
Câu 19:
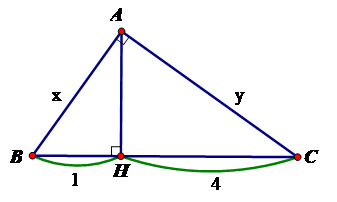
Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức lượng giữa cạnh và đường cao trong tam giác vuông ta có:
Áp dụng định lý Pytagp cho tam giác vuông AHB; AHC ta có:
AB = ; AC =
Vậy x = ; y = 2
Đáp án cần chọn là: C
Câu 20:
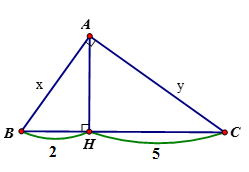
Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Áp dụng định lý Pytago cho tam giác vuông AHB, AHC ta có
AB = ;
AC =
Vậy x = ; y =
Đáp án cần chọn là: A
Câu 21:
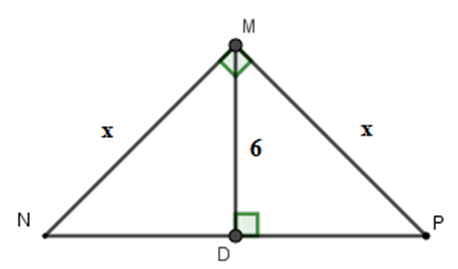
Tính x trong hình vẽ sau:
 Xem đáp án
Xem đáp án
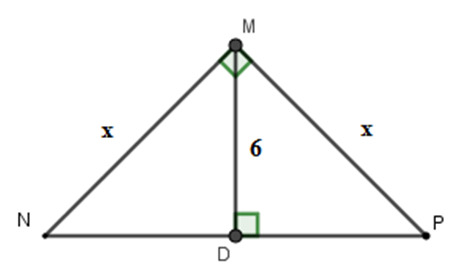
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x =
Đáp án cần chọn là: A
Câu 22:
Tính x trong hình vẽ sau:
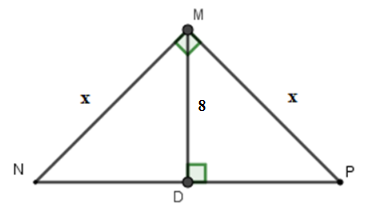
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x =
Đáp án cần chọn là: B
Câu 23:
Cho ABCD là hình tháng vuông A và D. Đường chéo BD vuông góc với BC. Biết AD = 12cm, DC = 25cm. Tính độ dài BC, biết BC < 20
 Xem đáp án
Xem đáp án
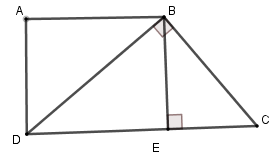
Kẻ BE CD tại E
Suy ra tứ giác ABED là hình chữ nhật (vì ) nên BE = AD = 12cm
Đặt EC = x (0 < x < 25) thì DE = 25 – x
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông BCD ta có:
<=> x(x – 16) – 9(x – 16) = 0 <=> (x – 16)(x – 9) = 0
(thỏa mãn)
Với EC = 16, theo định lý Pytago ta có BC = (loại)
Với EC = 9, theo định lý Pytago ta có BC = (nhận)
Vậy BC = 15cm
Đáp án cần chọn là: A
Câu 24:
Cho ABCD là hình thang vuông tại A và D. Đường chép BD vuông góc với BC. Biết AD = 10cm, DC = 20cm. Tính độ dài BC.
 Xem đáp án
Xem đáp án
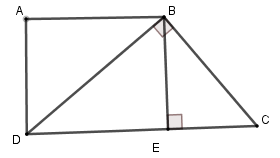
Kẻ BECD tại E
Suy ra tứ giác ABED là hình chữ nhật (vì ) nên BE = AD = 10cm
Đặt EC = x (0 < x < 20) thì DE = 20 – x
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông BCD ta có:
x(20 – x) = 100
x = 10 (tm)
Với EC = 10, theo định lý Pytago ta có BC =
Vậy BC =cm
Đáp án cần chọn là: B
Câu 25:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3 : 4 và AB + AC = 21. Tính các canh của tam giác ABC
 Xem đáp án
Xem đáp án
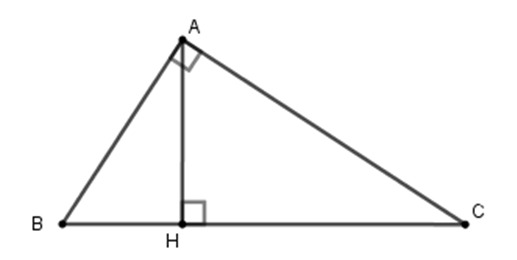
Theo giả thiết AB : AC = 3 : 4
Suy ra . Do đó AB = 3.3 = 9 (cm); AC = 3.4 = 12 (cm)
Tam giác ABC vuông tại A, theo định lý Pytago ta có:
, suy ra BC = 15cm
Đáp án cần chọn là: B
Câu 26:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 5 : 12 và AB + AC = 34. Tính các cạnh của tam giác ABC
 Xem đáp án
Xem đáp án
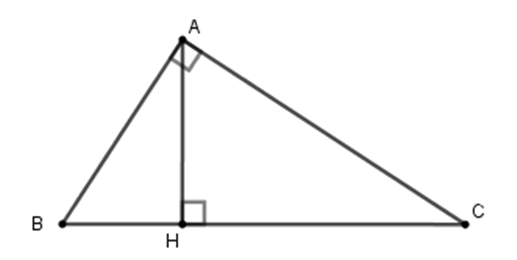
Theo giả thiết AB : AC = 5 : 12
Suy ra . Do đó AB = 5.2 = 10 (cm);
AC = 2.12 = 24 (cm)
Tam giác ABC vuông tại A, theo định lý Pytago ta có:
, suy ra BC = 26cm
Đáp án cần chọn là: C
Câu 27:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm, CH = 9cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
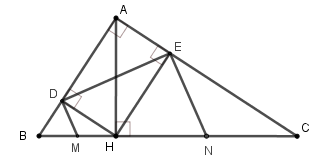
Tính độ dài đoạn thẳng DE
 Xem đáp án
Xem đáp án
Tứ giác ARHD là hình chữ nhật vì: nên DE = AH.
Xét ABC vuông tại A có = HB.HC = 4.9 = 36AH = 6
Nên DE = 6cm
Đáp án cần chọn là : D
Câu 28:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 9cm, CH = 16cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
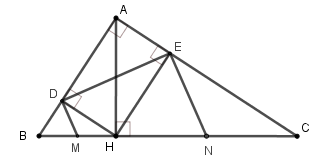
Tính độ dài đoạn thẳng DE.
 Xem đáp án
Xem đáp án
Tứ giác AEHD là hình chữ nhật vì: nên DE = AH.
Xét ABC vuông tại A có: = HB.HC = 9.16 = 144 => AH = 12
Nên DE = 12cm
Đáp án cần chọn là: A
Câu 29:
Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
 Xem đáp án
Xem đáp án
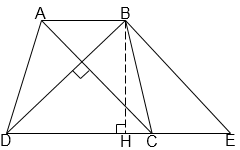
Qua B vẽ đường thẳng song song với AC, cắt DC ở E. Gọi BH là đường cao của hình thang. Ta có BE // AC, AC BD nên BE BD
Áp dụng định lý Pytago vào tam giác vuông BDH, ta có:
=> HD = 9cm
Xét tam giác BDE vuông tại B:
Ta có: AB = CE nên AB + CD = CE + CD = DE = 25cm
Do đó =(AB+CD).BH:2 = 25.12 : 2 = 150()
Đáp án cần chọn là: A
Câu 30:
Cho hình thang vuông ABCD () có hai đường chéo AC và BD vuông góc với nhau tại H. Biết HD = 18cm, HB = 8cm, tính diện tích hình thang ABCD
 Xem đáp án
Xem đáp án
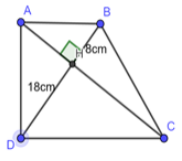
Xét ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
= HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
=> HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
- tứ giác có 2 đường chéo vuông góc với nhau thì S =
Đáp án cần chọn là: D
Câu 31:
Cho ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5cm; CK = 12cm. Tính BC, AB
 Xem đáp án
Xem đáp án
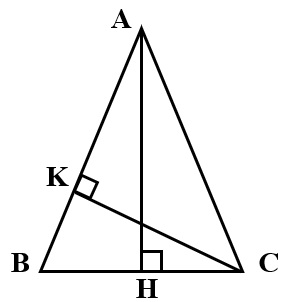
Ta có ∆ABC cân tại A => AH là đường cao đồng thời là đường trung tuyến (định lý)
=> H là trung điểm của BC
Đặt BH = x (x > 0, cm)
Ta có: AH.BC = CK.AB 7,5.2x = 12.AB
AB =
Áp dụng định lý Pitago cho ABH vuông tại H ta có:
=> AB = = 12,5 cm
=> BC = 2BH = 20cm
Đáp án cần chọn là: C
Câu 32:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N theo thứ tự là trung điểm AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH
 Xem đáp án
Xem đáp án
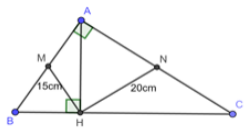
Xét ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABH vuông tại A có:
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
Đáp án cần chọn là: D
Câu 33:
Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN
 Xem đáp án
Xem đáp án
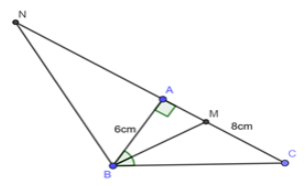
Áp dụng định lý Pitago cho ABH vuông tại A có:
Vì BM là tia phân giác trong của góc B (Tính chất đường phân giác)
MA = 3cm
Vì BM; BN là tia phân giác trong và ngoài của góc B
Áp dụng hệ thức lượng trong ABM vuông tại B có đường cao BA ta có:
Đáp án cần chọn là: D
Câu 34:
Cho tam giác ABC vuông tại A có cạnh AB = 30cm và AC = 40cm, đường cao AH, trung tuyến AM. Tính BH, HM, MC
 Xem đáp án
Xem đáp án
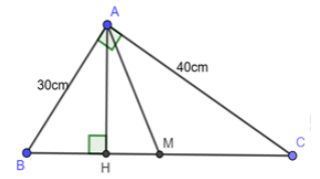
Áp dụng định lý Pytago cho ABH vuông tại A có:
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Vì AM là đường trung tuyến M là trung điểm BC
Ta có: MH = BM – BH = 25 – 18 = 7 cm
Đáp án cần chọn là: A
Câu 35:
Một tam giác vuông có cạnh huyền bằng 5, còn đường cao tương ứng cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
 Xem đáp án
Xem đáp án
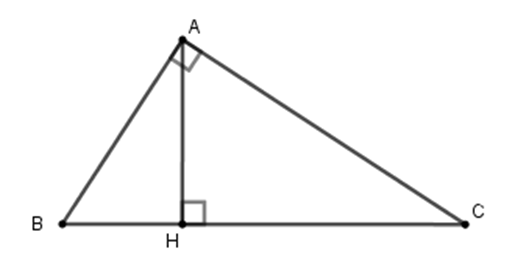
Giả sử tam giác đã cho là ABC vuông tại A có AB < AC, BC = 5; AH = 2
Đặt BH = x (0 < x < 2,5) => HC = 5 – x
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
=> (x – 1)(x – 4) = 0
Vậy cạnh nhỏ nhất của tam giác đã cho có độ dài là
Đáp án cần chọn là: A
Câu 36:
Cho ABC vuông tại A, các cạnh AB, AC tương ứng tỉ lệ với 3 và 4. Biết đường cao AH = 18.
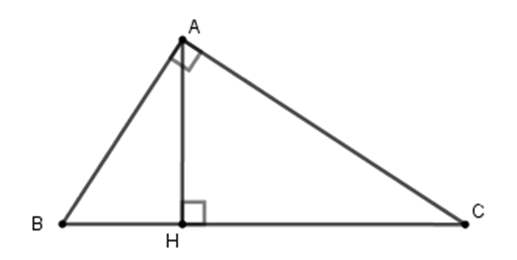
Tính chu vi ABC
 Xem đáp án
Xem đáp án
Theo đề bài ta có: các cạnh AB, AC tương ứng tỉ lệ với 3 và 4
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Áp dụng định lý Pitago cho ABC vuông tại A ta có:
Chu vi ABC: AB + BC + CA = 22,5 + 30 + 37, 5 = 90cm
Đáp án cần chọn là: A
Câu 37:
Cho ABC vuông tại A có AB = 3cm, AC = 4cm, đường cao AH và đường trung tuyến AM. Độ dài đoạn thẳng HM là:
 Xem đáp án
Xem đáp án
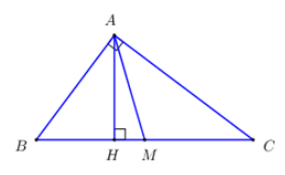
Áp dụng định lý Pytago trong tam giác vuông: ABC :
Áp dụng hệ thức lượng trong tam giác vuông ABC:
M là trung điểm củaBC
Vậy HM = BM – BH = (cm)
Đáp án cần chọn là: A
Câu 38:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, AH = 6cm. Tính độ dài các cạnh AC, BC của tam giác ABC.
 Xem đáp án
Xem đáp án
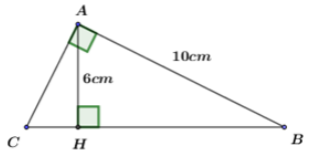
Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:
Trong tam giác vuông ABC vuông tại A có AH là đường cao
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
Vậy AC = 7,5 (cm); BC = 12,5 (cm)
Đáp án cần chọn là: B
