12 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 30 - Đề 1

Bài tập theo tuần Toán 9 - Tuần 30

Bài tập theo tuần Toán 9 - Tuần 30 - Đề 1

484 lượt thi
12 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

Cho hình 1. Biết sđ cung MQ (nhỏ) = 40 độ, sđ cung PN (nhỏ) = 60 độ. Ta có số đo góc PIN bằng: (ảnh 1)

Cho hình 1. Biết sđ $\overset{⏜}{M Q}$ (nhỏ) $= 40^{0}, s d \overset{⏜}{P N}$ (nhỏ) $= 60^{0} .$ Ta có số đo $\hat{P I N}$ bằng:

$A {.10}^{0}$

$B {.100}^{0}$

$C {.50}^{0}$

$D {.20}^{0}$

Xem đáp án

Chọn đáp án C

Câu 2:

AB là một dây cung của (O; R) và

s d \overset{⏜}{A B} = 80^{0}; M

là điểm trên cung nhỏ AB. Góc

\hat{A M B}

có số đo là :

$A {.80}^{0}$

$B {.140}^{0}$

$C {.160}^{0}$

$D {.280}^{0}$

Xem đáp án

Chọn đáp án B

Câu 3:

Cho hình 2. Biết góc xAB = 50 độ. Ta có số đo cung nhỏ AB bằng: (ảnh 1)

Cho hình 2. Biết $\hat{x A B} = 50^{0} .$ Ta có số đo cung nhỏ $\overset{⏜}{A B}$ bằng:

$A {.25}^{0}$

$B {.50}^{0}$

$C {.130}^{0}$

$D {.100}^{0}$

Xem đáp án

Chọn đáp án D

Câu 4:

Cho tứ giác ABCD nội tiếp đường tròn O và $\hat{D A B} = 80^{0} .$ Số đo cung $\overset{⏜}{D C B}$ là:

$A {.80}^{0}$

$B {.160}^{0}$

$C {.200}^{0}$

$D {.40}^{0}$

Xem đáp án

Chọn đáp án C

Câu 5:

Trong đường tròn (O; R). Cho $\hat{A O B} = 60^{0} .$ Số đo cung nhỏ AB bằng:

$A {.60}^{0}$

$B {.160}^{0}$

$C {.200}^{0}$

$D {.40}^{0}$

Xem đáp án

Chọn đáp án A

Câu 6:

Trong hình 3, biết x < y. Khẳng định nào dưới đây đúng ?

$A . M N = P Q$

$B . M N > P Q$

$C . M N < P Q$

$D . M P > N Q$

Xem đáp án

Chọn đáp án B

Câu 7:

Cho tứ giác MNPQ nội tiếp (O; R) và có $\hat{M} = 105^{0}$ và $\hat{N} = 70^{0} .$ Vậy số đo của

$\begin{array}{l} A . \hat{P} = 70^{0}; \hat{Q} = 105^{0} \end{array}$

$B . \hat{P} = 75^{0}; \hat{Q} = 110^{0}$

$C . \hat{P} = 105^{0}; \hat{Q} = 70^{0}$

$D . \hat{P} = 110^{0}; \hat{Q} = 75^{0}$

Xem đáp án

Chọn đáp án B

Câu 8:

Tứ giác ABCD nội tiếp đường tròn ;

\hat{C} = 2 \hat{A} .

Số đo các góc

\hat{C}

và

\hat{A}

là :

$\begin{array}{l} A . \hat{A} = 60^{0}; \hat{C} = 120^{0} \end{array}$

$B . \hat{A} = 30^{0}; \hat{C} = 150^{0}$

$C . \hat{A} = 120^{0}; \hat{C} = 60^{0}$

$D . \hat{A} = 45^{0}; \hat{C} = 135^{0}$

Xem đáp án

Chọn đáp án A

Câu 9:

Diện tích hình tròn có đường kính 20cm bằng:

$A .20 π c m^{2}$

$B .100 π c m^{2}$

$C .25 π c m^{2}$

$D .100 π c m^{2}$

Xem đáp án

Chọn đáp án B

Câu 10:

Công thức tính độ dài cung tròn $90^{0}$ là:

$A . l = \frac{π R n}{180}$

$B . l = \frac{π R^{2}}{4}$

$C . l = \frac{π R}{2}$

$D . l = \frac{π R}{4}$

Xem đáp án

Chọn đáp án C

Câu 11:

Cho hình vẽ bên dưới, có đường kính 10cm

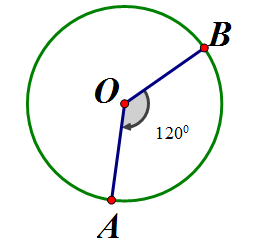
a) Tính chu vi đường tròn tâm O

b) Tính diện tích hình quạt tròn OAB

Xem đáp án

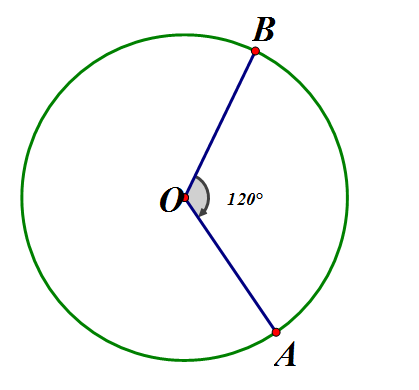
Cho hình vẽ bên dưới, có đường kính 10cm a) Tính chu vi đường tròn tâm O (ảnh 2)

Chu vi đường tròn $(O) : C = 2 π R = 10 π$

S quạt AOB

= \frac{π R^{2} n}{360} = \frac{π {.5}^{2} {.120}^{0}}{360^{0}} = \frac{25 π}{3} (c m^{2})

Câu 12:

Cho tam giác ABC có ba góc nhọn (AB < AC). Đường tròn tâm K đường kính BC cắt AB, AC theo thứ tự tại E và F. Biết BF cắt CE tại H

a) Chứng minh tứ giác AEHF nội tiếp và xác định tâm đường tròn ngoại tiếp tứ giác AEHF

b) Chứng minh $A E . A B = A F . A C$

c) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Tính tỉ số $\frac{O K}{B C}$ khi tứ giác OHBC nội tiếp.

Xem đáp án

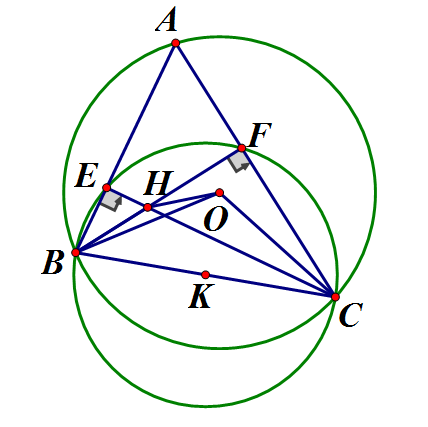
Cho tam giác ABC có ba góc nhọn (AB < AC). Đường tròn tâm K đường kính BC (ảnh 1)

a) Ta có $∠ B E C = ∠ B F C = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow ∠ A E H = ∠ A F H = 90^{0}$ (kề bù) $\Rightarrow ∠ A E H + ∠ A F H = 90^{0} + 90^{0} = 180^{0}$ nên tứ giác AEHF là tứ giác nội tiếp

b) Xét $Δ A F B$ và $Δ A E C$ có : $∠ A c h u n g; ∠ A E H = ∠ A F B = 90^{0}$

$\Rightarrow Δ A F B ~ Δ A E C (g - g) \Rightarrow \frac{A F}{A B} = \frac{A E}{A C}$ (hai cặp cạnh tương ứng tỉ lệ)

$\Rightarrow A F . A C = A B . A E (d f c m)$

c) Khi OHBC nội tiếp $\Rightarrow ∠ B H C = ∠ B O C$ mà $∠ B H C = ∠ E H F$ (đối đỉnh)

mà $∠ E A F + ∠ E H F = 180^{0}$ (tính chất tứ giác nội tiếp) nên $∠ E A C + ∠ B O C = 180^{0}$

mà $∠ B O C = 2 ∠ B A C$ (góc ở tâm và góc nội tiếp cùng chắn $\overset{⏜}{B C})$

$\Rightarrow ∠ B O C = 120^{0} \Rightarrow ∠ B O K = 60^{0}$

$Δ B O K$ vuông tại K (tính chất đường kính dây cung)

Ta có : $Δ B O K$ vuông tại K có $\hat{O} = 60^{0}$

$\Rightarrow \frac{O K}{B K} = \frac{1}{\sqrt{3}}$ mà $B C = 2 B K \Rightarrow B K = \frac{B C}{2}$

\begin{array}{l} \Rightarrow \frac{O K}{B K} = \frac{O K}{\frac{B C}{2}} = \frac{1}{\sqrt{3}} \\ \Leftrightarrow \frac{2 O K}{B C} = \frac{1}{\sqrt{3}} \Leftrightarrow \frac{O K}{B C} = \frac{1}{2 \sqrt{3}} = \frac{\sqrt{3}}{6} \end{array}

Bắt đầu thi ngay