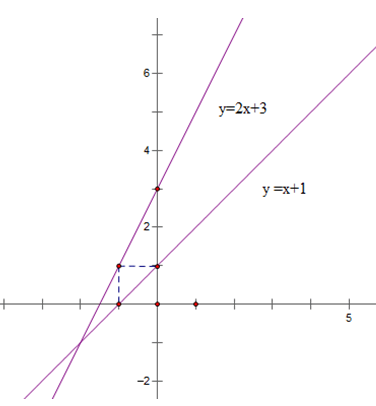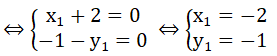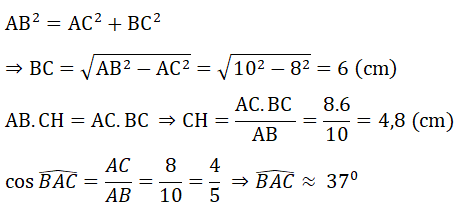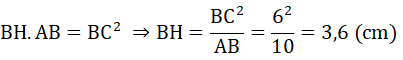18 câu hỏi trắc nghiệm thuộc Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án (Đề 5)

Câu 1:

Phần trắc nghiệm

Nội dung câu hỏi 1

$\sqrt{x - 5}$ có nghĩa khi:

A.x > 5

B.x ≥ 5

C.x < 5

D.x ≤ 5

Xem đáp án

Đáp án là B

Câu 2:

Biểu thức $\sqrt{{(x - 1)}^{2}}$ bằng:

A.x - 1

B.1 - x

C.|x - 1|

D. ${(x - 1)}^{2}$

Xem đáp án

Đáp án là C

Câu 3:

Giá trị của biểu thức $\sqrt{15 - 6 \sqrt{6}} + \sqrt{15 + 6 \sqrt{6}}$ bằng:

A.6

B.12 $\sqrt{6}$

C. $\sqrt{30}$

D.3

Xem đáp án

Đáp án là A

Câu 4:

Nếu đồ thị y = mx + 2 song song với đồ thị y = -2x + 1 thì:

A. Đồ thị hàm số y = mx + 2 cắt trục tung tại điểm có tung độ bằng 1

B. Đồ thị hàm số y = mx + 2 cắt trục hoành tại điểm có hoành độ bằng 2

C. Hàm số y = mx + 2 đồng biến

D. Hàm số y = mx + 2 nghịch biến

Xem đáp án

Đáp án là D

Câu 5:

Đường thẳng 3x – 2y = 5 đi qua điểm:

A. (1; - 1)

B. (5; -5)

C. (1; 1)

D. (-5; 5)

Xem đáp án

Đáp án là A

Câu 6:

Giá trị của biểu thức B = cos $62^{0}$ -sin $28^{0}$ là:

A. 2 cos $62^{0}$

B.0

C. 2 sin 28o

D. 0,5

Xem đáp án

Đáp án là B

Câu 7:

Cho (O; 6cm) và đường thẳng a. Gọi d là khoảng cách từ tâm O đến a. Điều kiện để a cắt (O) là:

A. Khoảng cách d > 6cm

B. Khoảng cách d = 6 cm

C. Khoảng cách d ≥ 6cm

D. Khoảng cách d < 6 cm

Xem đáp án

Đáp án là D

Câu 8:

Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng:

A. $\frac{R}{2}$

B. $\frac{R \sqrt{3}}{2}$

C. $R \sqrt{3}$

D. $R \sqrt{2}$

Xem đáp án

Đáp án là C

Câu 9:

Phần tự luận

Nội dung câu hỏi 1

Cho biểu thức:

$P = \frac{\sqrt{x} + 1}{\sqrt{x} + 2} + \frac{3 \sqrt{x} + 2}{x - 4}$

$Q = \frac{x - 5 \sqrt{x} + 6}{x + 2 \sqrt{x}}$ với x > 0, x khác 4

a) Rút gọn biểu thức P

Xem đáp án

a) Với x > 0; x ≠ 4,ta có:

Câu 10:

Cho biểu thức:

$P = \frac{\sqrt{x} + 1}{\sqrt{x} + 2} + \frac{3 \sqrt{x} + 2}{x - 4}$

$Q = \frac{x - 5 \sqrt{x} + 6}{x + 2 \sqrt{x}}$ với x > 0, x khác 4

b) Tính giá trị của biểu thức Q tại x = 9

Xem đáp án

Câu 11:

Cho biểu thức:

$P = \frac{\sqrt{x} + 1}{\sqrt{x} + 2} + \frac{3 \sqrt{x} + 2}{x - 4}$

$Q = \frac{x - 5 \sqrt{x} + 6}{x + 2 \sqrt{x}}$ với x>0, x khác 4

c) Tìm các giá trị x để M = P. Q có giá trị âm.

Xem đáp án

Câu 12:

Cho đường thẳng $d_{1}$ :y = mx + 2m - 1 (với m là tham số) và $d_{2}$ : y = x + 1

a) Với m = 2. Hãy vẽ các đường thẳng $d_{1}$ và $d_{2}$ trên cùng một mặt phẳng tọa độ. Tìm tọa độ gia điểm của hai đường thẳng $d_{1}$ và $d_{2}$

Xem đáp án

Với m = 2 thì $d_{1}$ : y = 2x + 3; $d_{2}$ : y = x + 1

Tập xác định của hàm số R

Bảng giá trị

x	0	- 1
y = 2x + 3	3	1

x	0	- 1
y = x + 1	1	0

Gọi A ( $x_{0}$ ; $y_{0}$ ) là tọa độ giao điểm của d1 và d2

Khi đó:

( $y_{0}$ = 2 $x_{0}$ + 3 và $y_{0}$ = $x_{0}$ + 1

⇒ 2xo + 3 = $x_{0}$ + 1 ⇔ $x_{0}$ = -2

⇒ $y_{0}$ = $x_{0}$ + 1 = -2 + 1 = -1

Vậy tọa độ giao điểm của $d_{1}$ và $d_{2}$ là (-2; -1)

Câu 13:

Cho đường thẳng $d_{1}$ :y = mx + 2m - 1 (với m là tham số) và $d_{2}$ : y = x + 1

b) Tìm giá trị của m để đường thẳng $d_{1}$ cắt trục hoành tại điểm có hoành độ bằng – 3.

Xem đáp án

b) $d_{1}$ cắt trục hoành tại điểm có hoành độ bằng – 3 khi:

0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1

Vậy với m = -1 thì $d_{1}$ cắt trục hoành tại điểm có hoành độ bằng – 3

Câu 14:

Cho đường thẳng $d_{1}$ :y = mx + 2m - 1 (với m là tham số) và $d_{2}$ : y = x + 1

c) Chứng mình rằng đường thẳng $d_{1}$ luôn đi qua một điểm cố định với mọi giá trị của m.

Xem đáp án

c) Giả sử đường thẳng $d_{1}$ luôn đi qua một điểm cố định ( $x_{1}$ ; $y_{1}$ ) với mọi giá trị của m.

⇒ $y_{1}$ = m $x_{1}$ + 2m - 1 với mọi m

⇔ m( $x_{1}$ + 2) - 1 - $y_{1}$ = 0 với mọi m

Vậy điểm cố định mà $d_{1}$ luôn đi qua với mọi giá trị của m là (-2; -1).

Câu 15:

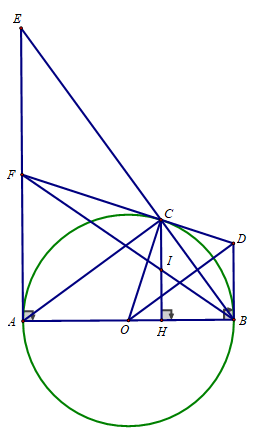
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)

a) Chứng minh tam giác ABC vuông. Tính độ dài CH và số đo ∠(BAC) (làm tròn đến độ)

Xem đáp án

a) Tam giác ABC nội tiếp (O) có AB là đường kính

⇒ ∠(ACB) = 90o

Hay tam giác ABC vuông tại C

Tam giác ABC vuông tại C, CH là đường cao có:

Câu 16:

Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)

b) Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại D. Chứng minh OD ⊥ BC

Xem đáp án

b) DC và DB là 2 tiếp tuyến cắt nhau tại D

⇒ DC = DB

Lại có: OC = OB = R

⇒ OD là đường trung trực của BC hay OD ⊥ BC

Câu 17:

Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)

c) Tiếp tuyến tại A của đường tròn (O) cắt BC tại E. Chứng minh:CE.CB = AH. AB

Xem đáp án

c) Xét tam giác ACB vuông tại C, CH là đường cao nên :

AH.AB = $A C^{2}$

Xét tam giác ABE vuông tại A, AC là đường cao nên :

EC.BC = $A C^{2}$

⇒ AH.AB = EC.BC

Câu 18:

Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)

d) Gọi I là trung điểm của CH. Tia BI cắt AE tại F. Chứng minh: FC là tiếp tuyến của đường tròn (O).

Xem đáp án

d) Xét tam giác ACB vuông tại C, CH là đường cao nên :

Xét tam giác ABE vuông tại A, AC là đường cao nên :

⇒ EA = 2 FA ⇒ F là trung điểm của EA

Tam giác CEA vuông tại C có CF là trung tuyến

⇒ FC = FA

⇒ ΔFCA cân tại F ⇒ ∠(FCA) = ∠(FAC)

Lại có ΔOCA cân tại O ⇒ ∠(OCA) = ∠(OAC)

⇒ ∠(FCA) + ∠(OCA) = ∠(FAC) + ∠(OAC)

⇔ ∠(FCO) = ∠(FAO) = $90^{0}$

Vậy FC ⊥ CO hay FC là tiếp tuyến của (O)